- 9.4. Модифицированная модель оценки доходности финансовых активов
- Методы оценки ценных бумаг
- Оценка ожидаемой доходности
- Оценка на основе непрерывного прироста дивидендов
- Модифицированная модель оценки
- Модифицированная модель оценки капитальных активов MCAPM на российском фондовом рынке
- Оценка эффективности инвестиционного портфеля, сформированного по алгоритму Г. Марковица, модифицированного фундаментальными моделями доходности ценных бумаг
- Библиографическое описание:
9.4. Модифицированная модель оценки доходности финансовых активов
Предположим, рынок капитала, как и прежде (рис. 1.3), представлен ценными бумагами по соотношению риск-доходность. Пусть действительна сформулированная ранее система ограничений и допущений, в которую внесем изменение. Исключим возможность осуществления безрисковых операций, т.е. отменим условия 15, 17 из числа характеристик идеального рынка (табл. 2.2), что соответствует реальному состоянию внешней финансовой среды заключения сделок (рис. 1.2). В силе остаются свойства 2-5, 9, 10, 12, 13, 16 из числа характеристик совершенного рынка капитала (табл. 2.2).
Используя логику рассмотренного выше подхода, определим, как инвесторы на основе хорошо диверсифицированного портфеля m (рис. 1.2), создают различающиеся по соотношению риск-доходность сочетания ценных бумаг. Если рыночный субъект предпочитает относительно более надежный портфель (фактическая доходность которого не подвержена значительным колебаниям), то для снижения риска следует приобрести финансовые активы b и/или продать j. С другой стороны, инвестору, рассчитывающему получить большую ожидаемую доходность, наоборот, необходимо снизить долю ценных бумаг b и увеличить удельный вес j. В первом случае участник рынка капитала потеряет в ожидаемой доходности. Во втором случае субъект столкнется с более высоким финансовым инвестиционным риском. При этом расходиться в величинах риска и ожидаемой доходности данные субъекты будут по прямой линии bmj, которая и определяет эффективное множество портфелей (рис. 1.2).
Наконец, дадим математически формализованное выражение модели оценки доходности финансовых активов (рис. 1.2), т.е. укажем, как рассчитать требуемую норму прибыли ценных бумаг, например, j, если положить в основу анализа уравнение линейной регрессии Y=b+aX. Используя правила теории геометрических пропорций, обозначим Y=Rj, причем bRrf, т.к. безрисковой доходности не существует, однако допустимо, что b=Řb, тогда a=(Řm-Řb)/(p-b), соответственно, X=j-b. В общем, подставим все компоненты в Y=b+aX и получим модернизированную ценовую модель фондового рынка (рис. 1.2):
Однако надо устранить сомнения в корректности предположения о линейном характере зависимости доходности от риска, когда отсутствует безрисковая ставка, которая не коррелирует, как это показано в моделях (3.22), (3.23), ни с одной другой доходностью. Для этого вычтем из формулы (3.23) запись (3.22), но для начала выразим безрисковую доходность с помощью уравнения (3.22) и подставим ее в полученную разность:
Источник
Методы оценки ценных бумаг
Оценка ценных бумаг имеет свою специфику, которая обуславливаются тем, что данный вид активов представляет собой особую форму существования капитала и вместе с тем является товаром на фондовом рынке. С целью оценки стоимости используются различные методы оценки ценных бумаг.
Методика определения справедливой стоимости ценных бумаг подразумевает вычисление их ценности как финансового актива, приносящего доход своему владельцу. При этом в обязательно порядке применяются не только российские стандарты оценки, но и международные стандарты оценки (МСО), а основной цель такой оценки является подтверждение стоимости при формировании финансовой отчетности по международным стандартам (МСФО/IFRS).
На сегодняшний день наиболее широко используемыми являются следующие методы оценки стоимости ценных бумаг:
- метод ожидаемой доходности;
- оценка на основе прироста дивидендов;
- модифицированная модель.
Оценка ожидаемой доходности
Оценка стоимости ценных бумаг по ожидаемой доходности является наиболее широко используемой. Этот метод базируется на анализе планируемого дохода, от владения ценной бумагой. Доходность рассчитывается с учетом двух компонентов:
- дивидендов;
- увеличения курсовой стоимости.
Этот метод определения стоимости ценных бумаг предполагает анализ выплаченных дивидендов за предыдущие периоды и динамики курсовой стоимости. При этом ожидаемая доходность сопоставляется с фактической. Также учитываются возможные риски от вложений.
Оценка на основе непрерывного прироста дивидендов
Данный метод может быть использован при оценке стоимости акций. При этом устанавливаются определенные допущения:
- стабильность ежегодного темпа прироста дивидендных выплат;
- темп увеличения дивидендов является отражением темпов роста предприятия и его активов;
- необходимая доходность превышает темп роста дивидендов.
Применение метода для оценки ценных бумаг компаний Москвы или других городов имеет существенный недостаток, который заключается в том, что рост дивидендов не всегда адекватно отображает реальный рост компании. Предприятие или организация может выплачивать высокие дивиденды за счет снижения части прибыли, направленной на развитие бизнеса, что замедляет темпы роста компании.
В противоположном случае возможно сокращение размеров дивидендных выплат с целью использования чистой прибыли для обеспечения развития компании и увеличения доходности ее активов.
Модифицированная модель оценки
Эта модель применяется с целью нивелирования недостатков предыдущего метода. В данном случае дополнительно учитываются возможности реинвестирования прибыли, и рассчитывается возможный уровень доходности. Также во внимание берется эффективность инвестирования средств.
Независимая оценка ценных бумаг с использованием модифицированного метода позволяет использовать коэффициенты, характеризующие уровень доходности реинвестированных средств. В результате удается получить более достоверные значения. Так как эффективно инвестированная прибыль в дальнейшем приносит увеличение прибыльности и соответственно рост потоков дивидендных выплат.
Таким образом, использование модифицированной модели на практике позволяет получить более адекватную и обоснованную оценку и сделать верные выводы о целесообразности покупки ценных бумаг.
Источник
Модифицированная модель оценки капитальных активов MCAPM на российском фондовом рынке
Модель оценки капитальных активов была предложена У. Шарпом еще в 1961 году. После этого вышло множество дополнений и уточнений этой модели.
Теория оценки акций предполагает, что премия за риск пропорциональна самому риску, который выражен как коэффициент бета. У. Шарп разделил риск портфеля на два вида: систематический риск и несистематический риск. Систематический риск еще называют рыночным риском или недиверсифицируемым риском, он обусловлен общим движением рынка или его сегментов и не связан с конкретной ценной бумагой. Несистематические риски (диверсифицируемые риски) – это риски которые случайно возникают в компании, но которые можно уменьшить за счет диверсификации.
Одной из модификаций модели У.Шарпа есть модель MCAPM – модифицированная модель оценки капитальных активов. MCAPM в отличии от CAPM использует дополнительный показатель, который учитывает специфические несистематические риски компании. Это особо актуально для российского фондового рынка, для которого характера высокая нестабильность. Это требует использование более точных методов оценки капитала компании.
Формула расчета MCAPM 
Где:
R- ожидаемая норма доходности;
Rf – безрисковая ставка доходности, как правило, ставка по государственным облигациям;
Rd– доходность рынка;
Ru– рисковая премия, учитывающая несистематические риски оцениваемой компании;
β- коэффициент бета, который является мерой рыночного риска (недиверсифицируемого риска) и отражает чувствительность доходности ценной бумаги к изменениям доходности рынка в целом.
Проведем анализ российской компании на основе модели MCAPM
Проведем анализ и оценим стоимость компании ОАО «Негуснефть». Для этого рассчитаем все необходимые значения коэффициентов. За безрисковую ставку доходности, как правило, берут доходность инвестиций в 10-летние ОГВЗ. Ставка доходности составляет 5,04%.
Доходность рынка представляет собой доходность рыночного индекса ММВБ (MICEX) или РТС (RTSI).
Для того что бы определить премию за несистематические риски воспользуемся экспертными оценками. Премии за каждый вид несистематического риска оценивается в диапазоне от 0 до 1%. Ниже представлена экспертная оценка рисков.
Виды несистематических рисков
Премия за риск, %
Зависимость от государственного регулирования тарифов на продукцию предприятия
Источник
Оценка эффективности инвестиционного портфеля, сформированного по алгоритму Г. Марковица, модифицированного фундаментальными моделями доходности ценных бумаг
Рубрика: Экономика и управление
Дата публикации: 18.11.2015 2015-11-18
Статья просмотрена: 1419 раз
Библиографическое описание:
Кашина, О. И. Оценка эффективности инвестиционного портфеля, сформированного по алгоритму Г. Марковица, модифицированного фундаментальными моделями доходности ценных бумаг / О. И. Кашина. — Текст : непосредственный // Молодой ученый. — 2015. — № 22 (102). — С. 400-402. — URL: https://moluch.ru/archive/102/23533/ (дата обращения: 11.06.2021).
В условиях рыночной экономики рациональное формирование инвестиционного портфеля позволяет инвестору получить доход и увеличить свое будущее благосостояние. Однако эффективность портфельных инвестиции напрямую зависит от способности инвесторов быстро и адекватно реагировать на изменения состояния российского финансового рынка для определения оптимальной структуры портфеля. В подобных условиях известные классические подходы [7, 9] к принятию оптимального инвестиционного решения зачастую становятся неэффективными и требуют корректировки. Применение компьютерной обработки информации для реализации моделей инвестиционного портфеля увеличивают оперативность принятия решений.
В настоящей работе рассматривается возможность модификации подхода Г. Марковица [9] с помощью фундаментальных моделей доходности [1–3, 8], оценивается эффективность данной модификации.
Основная идея портфельной теории Г. Марковица заключается в том, что координаты оптимального портфеля инвестора соответствуют точке касания его кривых безразличия эффективного множества [9]. Эффективное множество определяется Г. Марковицем как множество портфелей, которые обеспечивают минимальный риск при фиксированном уровне ожидаемой доходности, и максимальную ожидаемую доходность при определенном уровне риска [9]. Однако некоторые из предположений (например, однородность ожиданий инвесторов), на которых основывается подход Г. Марковица, не соответствуют реалиям рыночной торговли ценными бумагами, что неоднократно освещалось в ряде работ (например, в [5–6]).
В классической портфельной теории ожидаемую доходность принято определять как среднее значение фактических доходностей:
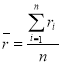
где 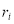
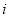
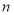
Формула (1.1) вытекает из нормального закона распределения случайных величин. Вместе с тем многочисленные исследования (например, в [4]) показывают, что доходности большинства российских финансовых активов не распределены нормально.
Методики определения ожидаемой доходности акций, известные в фундаментальном анализе основываются на изучении информации о текущем положении и перспективах развития компании, публикуемых в финансовой отчетности. Результаты данного анализа позволяют выбрать оптимальный состав портфеля ценных бумаг. В фундаментальном анализе известно несколько подходов к определению ожидаемой доходности ценных бумаг. Подробнее остановимся на наиболее известных фундаментальных моделях.
- Определение ожидаемой доходности акций
через коэффициент
[1–2]
В фундаментальном анализе широко известна следующая модель:
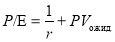
где 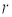
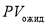
Предполагая, что ожидаемые перспективы роста стоимости акций равны нулю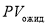
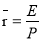
- Определение ожидаемой доходности акций
на основе модели Гордона [8]
Модель Города [8] применяется для определения текущей стоимости актива (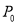
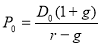
где 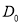
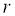
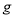
Соответственно, ожидаемая доходность акций может быть определена по формуле:
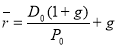
- Определение ожидаемой доходности акций
через текущее и справедливое значение коэффициента
с учетом вероятного горизонта инвестирования (3 года) [2].
Ожидаемая доходность акций 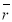
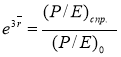
где 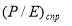
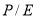
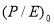
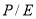
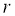
Откуда, ожидаемая доходность акций компании:
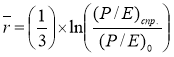
В качестве исходных данных для оценки эффективности инвестиционного портфеля, сформированного по алгоритму Г. Марковица, модифицированного фундаментальными моделями доходности ценных бумаг на российском финансовом рынке выступали данные о ценах высоколиквидных акций российских компаний [10] за период 01.01.2014–01.01.2015 гг. Для диверсификации портфеля были выбраны акции семи компаний, представляющих разные отрасли экономики: ОAO «Лукойл», ОAO «Группа компаний ПИК», ОAO «Норильский Никель», ОAO «ВТБ», ОAO «Татнефть», ОAO «Росбанк», ОAO «Магнит» [10]. По данным фондовым активам рассчитывались ожидаемые доходности по формуле (1) и риск, а также коэффициент корреляции между ними.
Затем определялось достижимое и эффективное множество портфелей ценных бумаг в соответствии с классическим алгоритмом Г. Марковица [9]. Методика выбора оптимального портфеля основывалась на подходе Г. Марковица [9], дополненного идеями У. Шарпа [7]. Выбор оптимального портфеля осуществлялся графическим способом путем совмещения на одном графике эффективной границы Г. Марковица и линии, выходящей из точки безрисковой ставки, на которой располагаются портфели, включающие рискованные и безрисковые финансовые активы. Таким образом, были получены координаты (риск, доходность) оптимального портфеля и определен его состав. Так, было выяснено, что наиболее эффективным портфелем является портфель, на 90 % состоящий из акций ОAO «Группа компаний ПИК» и на 10 % — из акций ОАО «ВТБ». Инвестиционные характеристики — ожидаемая доходность и риск данного портфеля приведены в таблице 1.
Далее проводилась модификация подхода Г. Марковица [9] с помощью фундаментальных моделей доходностей. По исследуемым фондовым активам последовательно рассчитывалась их ожидаемая доходность по формулам (3), (5) и (7) и в соответствии с классическим алгоритмом Г. Марковица [9], описанным выше и дополненным идеями У. Шарпа [7], определялся оптимальный портфель ценных бумаг.
Инвестиционные характеристики полученных оптимальных портфелей представлены в таблице 1.
Инвестиционные характеристики оптимальных портфелей, полученных при использовании алгоритма Г. Марковица, а также его модификаций с помощью фундаментальных моделей доходностей
Методика
Ожидаемая доходность, (%)
Риск, (%)
Алгоритм Г. Марковица
Алгоритм Г. Марковица, модифицированный фундаментальной моделью доходности, выраженной через текущее и справедливое значение коэффициента 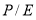
Алгоритм Г. Марковица, модифицированный фундаментальной моделью доходности, выраженной через коэффициент 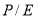
Алгоритм Г. Марковица, модифицированный фундаментальной моделью доходности Гордона (5)
Из таблицы 1 видно, что наиболее привлекательными инвестиционными характеристиками обладает оптимальный портфель, построенный с помощью алгоритма Г. Марковица, модифицированного моделью доходности, выраженной через текущее и справедливое значение коэффициента 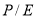
Вместе с тем, портфель ценных бумаг, отобранный по алгоритму Г. Марковица, также демонстрирует высокую эффективность.
Сопоставление представленных в таблице 1 инвестиционных характеристик оптимальных портфелей с их фактическими значениями показало, что именно указанные портфели (оптимальный портфель по Г. Марковицу и портфель, построенный с помощью алгоритма Г. Марковица, модифицированного моделью доходности, выраженной через текущее и справедливое значение коэффициента 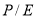
Таким образом, на основе произведенных расчетов, можно сделать вывод о том, что наиболее эффективной методикой для построения оптимального портфеля является алгоритм Г. Марковица [9] и его модификация с помощью фундаментальной модели (7) [2].
1.Брейли, Р. Принципы корпоративных финансов / Р. Брейли, С. Майерс; пер. с англ. Н. Н. Барышниковой. — М.: Олимп-бизнес, 2008. — 1008 с.
2.Грэхем Б., Додд Д. Анализ ценных бумаг / Б. Грэхем, Д. Додд; пер. с англ. — М.: Вильямс, 2015. — 880 с.
3.Кашина О. И. Об использовании анализа дивидендной доходности с целью совершенствования инвестиционных стратегий на финансовом рынке / О. И. Кашина // Молодой ученый. — 2014. — № 21 (80). — С. 332–335.
4.Некрасова, И. В. Определение степени эффективности российского фондового рынка на современном этапе функционирования / И. В. Некрасова // Вопросы регулирования экономики. — 2010. — Т. 1, № 2. — С. 5–16.
5.Петров С. С., Кашина О. И. О возможностях прогнозирования доходности финансовых активов на основе анализа биржевых котировок / С. С. Петров, О. И. Кашина // Аудит и финансовый анализ. — 2015. — № 2. — С. 135–140.
6.Петров С. С., Кашина О. И. Оптимизация активной стратегии управления портфелем ценных бумаг по критериям ожидаемой доходности и риска / Петров С. С., Кашина О. И. // Аудит и финансовый анализ. — 2013. — № 2. — С. 217–227.
7.Шарп У. и др. Инвестиции / Уильям Ф. Шарп, Гордон Дж. Александер, Джэффри В. Бэйли; пер. с англ. — М.: ИНФРА-М, 2001. — XII, 1028 с.
8.Gordon M. J. Dividends, Earnings, and Stock Prices / M. J. Gordon // The Review of Economics and Statistics. — 1959. — Vol. 41. — № 2, Part 1. — Р. 99–105.
9.Markowitz H. Portfolio selection / H. Markowitz // Journal of finance. — 1952. — Vol. 7. — No. 1. — P. 77–91.
Источник





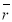 через коэффициент
через коэффициент 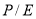 [1–2]
[1–2]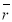 на основе модели Гордона [8]
на основе модели Гордона [8]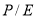 с учетом вероятного горизонта инвестирования (3 года) [2].
с учетом вероятного горизонта инвестирования (3 года) [2].