Постановка и решение задачи оптимального распределения инвестиций
Экономическая эффективность капитальных вложений (инвестиций) — одна из важнейших проблем планирования, характеризующая целесообразность вложений финансовых и других средств.
Рационального распределения инвестиций можно достигнуть лишь на основе тщательных экономических расчетов, дающих возможность определить пути достижения максимальной отдачи, т.е.
При установлении структуры инвестиций на государственном уровне необходимо исходить из предусмотренных темпов развития отраслей экономики страны, обеспеченности их основными фондами и степени использования мощностей, объема сырья и материалов, поступающих из смежных отраслей, и ряда других факторов.
Межотраслевое распределение инвестиций должно сопровождаться распределением вложений внутри отрасли и, в частности, между предприятиями, выпускающими однородную продукцию. Критерием для оптимального распределения инвестиций могут служить максимальная прибыль, максимальный суммарный прирост продукции, максимальное снижение себестоимости, максимальная занятость населения и т.п.
Задача оптимального распределения инвестиций по своей природе комбинаторная. Например, при определении фондоотдачи от 10 млрд руб. в четыре отрасли промышленности необходимо перебрать все распределения числа 10 на четыре группы. При условии распределения только из целых чисел необходимо подсчитать 286 комбинаций:
(10, 0, 0, 0); (9, 1, 0, 0); (9, 0, 1, 0); (9, 0, 0, 1) . ;
(8, 1, 1, 0); (8, 1, 0, 1); (8, 0, 1, 1); (8, 2, 0, 0); (8, 0, 2, 0); (8, 0, 0, 2);
(4, 3, 2, 1); . (4, 2, 2, 2); .
Если требуется дополнительно определить оптимальное решение задачи в случае, когда инвестиции в целом составляют 9, 8, 7, . 1 млрд руб., то необходимо провести большой объем вычислительной работы.
Метод динамического программирования позволяет находить оптимальное решение задач по распределению однородных средств между объектами при значительно меньшем, по сравнению с комбинаторным способом решения, объеме вычислительной работы.
В общем виде математическая постановка задач по распределению однородных средств (капитальных вложений, машин, сырья и т.д.) между объектами формулируется следующим образом: найти значения неизвестных xv х2, . х, . хп, т.е. план распределения, удовлетворяющий условиям:
обращающие в максимум функцию
(4.2)
где— сумма возможных вложений по j-му объекту (отрасль, пред
приятие, цех, участок);
— фондоотдача по предполагаемому j-му объекту, т.е. функция 
отдачи капитальных вложений (прибыль, прирост продукции и т.д.).
Алгоритм, предложенный Беллманом, справедлив для функций
любого вида и является одним из простейших примеров применения динамического программирования. Идея алгоритма состоит в том, что последовательно решаются задачи оптимального распределения средств между первыми j объектами (здесь j принимает значения 1, 2, 3, . n). Последняя из этих задач является решением поставленной.
В задаче по распределению средств между объектами всегда предполагаются известными значения функций f.(x) при всех возможных значениях аргументов (табл. 4.7).
Источник
Динамическое программирование. Задача о распределении инвестиций — видеоурок с решением задачи в Excel
>Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и xls в архиве zip, начнется автоматически через 10 секунд. Видеоурок по решению этих задач — внизу страницы.
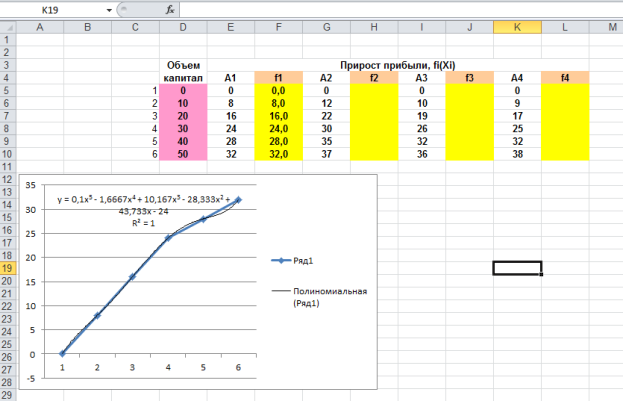
Указать оптимальные размеры и потоки инвестирования, если прибыль от вложений (Х i ) в проекты (А i ) распределилась следующим образом:
Теперь для решения этой задачи воспользуемся Excel .
Для этого выделим шаги тренда t i , вложения x i и прибыли A i . Затем для каждого из четырех проектов построим средствами MS Excel графическую зависимость прибыли А от шага тренда ( t = 1, 2, 3, 4, 5 , 6 ). Активизируем точки графика, щелкнув по ним левой клавишей мыши, затем нажмем правую клавишу и выберем режим «Добавить линию тренда» . Для всех четырех проектов наилучшим типом является полиномиальный 5 -о й степени. С помощью полученных уравнений трендов находим теоретические значения прибыли при различных значениях шага тренда t i . Уравнения моделей тренда, коэффициенты аппроксимации и теоретические значения при были, представлены на рисунке 1.
Рис. 1. Графические зависимости прибыли от вложений и полиномиальные тренды этих зависимостей.
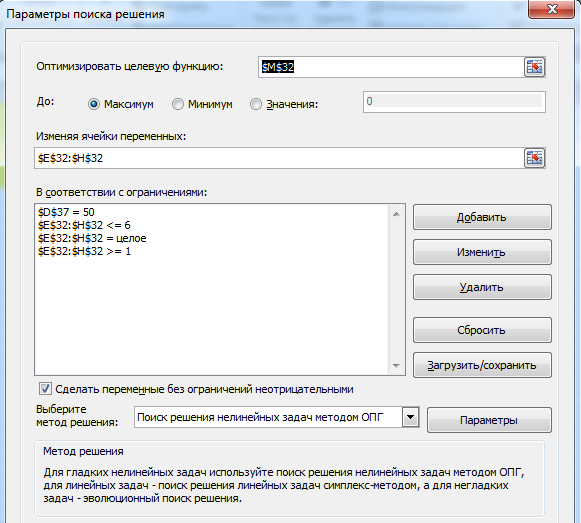
В ячейку М32 вводим выражение для общей (суммарной) прибыли, которую надо максимизировать, — это сумма всех четырех полиномиальных функций. Зависимыми переменными в этой функции являются искомые значения шагов тренда, которые будут располагаться в ячейках E 32 — H 32 . Суммарные вложения не должны превышать 5 0 тыс. ед., следовательно, вводим ограничение 1 0 *(E32+F32+G32 +H32 -4) в ячейку D 37 .
Выбираем из главного меню MS Excel режим «Поиск решения» и заполним открывшееся диалоговое окно в соответствии с требованиями. Нажмем клавишу «выполнить» и получим результат оптимизации.
Рис. 2. Модель максимизации прибыли.
Рис. 3. Оптимальное распределение капиталовложений между проектами.
Имя файла: dinprogr.zip
Размер файла: 129.98 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
Источник
ЗАДАЧА ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИЙ ПО ПРОЕКТАМ
ЗАНЯТИЕ 3
ТРАНСПОРТНАЯ ЗАДАЧА
Словесная формулировка. Имеется 
поставщиков А1, А2 , … , Аm некоторого однородного грузас запасами a1, a2,…,am соответственно. Имеется 
потребителей B1, B2,… , Bn этого груза c заявками b1, b2,…,bn. Заданы тарифы перевозок 
, означающие стоимости перевозки единицы груза от Ai к Bj ; кроме того, заданы штрафные тарифы 
, означающие издержки, вызываемые каждой единицей невывезенного груза поставщиков 
, 
, а также штрафные тарифы 
, означающие издержки, вызываемые каждой единицей недопоставленного груза потребителям 
, 
. Требуется составить такой план перевозки грузов, при котором: 1) объемы вывозимых грузов не превышают запасы поставщиков; 2) объемы поставок не превышают заявки потребителей; 3) суммарные издержки всех перевозок минимальны.
Формальная постановка. Используя введенные обозначения, имеем:
(2.1)
(2.2)
Задача 2.1.Имеется пять поставщиков и пять потребителей некоторого груза. Стоимости перевозки единицы груза сij от i-го поставщика к j-му потребителю, данные о возможностях поставщиков и запросах потребителей, а также штрафы за недопоставку/невывоз каждой единицы груза, представлены в следующих таблицах:
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | Потребитель 5 | Штрафы за невывоз |
| Поставщик 1 | |||||
| Поставщик 2 | |||||
| Поставщик 3 | |||||
| Поставщик 4 | |||||
| Поставщик 5 |
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | Потребитель 5 |
| Штрафы за недопоставку |
| Поставщик 1 | Поставщик 2 | Поставщик 3 | Поставщик 4 | Поставщик 5 |
| Возможности поставщиков |
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | Потребитель 5 |
| Запросы потребителей |
Каждый поставщик заинтересован поставить весь имеющийся у него груз, каждый потребитель – максимально удовлетворить свои потребности. Составить оптимальный план перевозок с минимальной стоимостью.
Решение: 1) переписываем «возможности поставщиков» в столбец как «запасы»;
2) переписываем «запросы потребителей» как «потребности»
3) подсчитываем (в ячейках В9 и I2) суммарные запасы и суммарные потребности, определяя после этого тип задачи (закрытая, на избыток или на недостаток);
4) подсчитываем кол-во вывезенного (В18:В22), привезенного (D16:H16) груза, остатки у поставщиков (J18:J22) и недопоставки у потребителей (D24:H24);
5) подсчитываем издержки (B13; D13; F13; H13); 7) вызываем «Поиск решения» и решаем задачу:
Рис 2.1. Шаблон с решением задачи 2.1
Задачи для самостоятельного решения
Задача 2.2. Для строительства 4-х объектов используется кирпич, изготовляемый на трех заводах. Ежедневно на заводе1, заводе2 и заводе3 может изготовляться соответственно 100, 150 и 50 тыс. шт. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов равны 75, 80, 60 и 85 тыс. шт. Известны также тарифы перевозок 1 тыс. шт. кирпича с каждого завода к каждому из строящихся объектов:
| Объект1 | Объект2 | Объект3 | Объект4 |
| Завод1 | |||
| Завод2 | |||
| Завод3 |
Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок является минимальной. Чему она равна? Ответ: Fmin=665 при X * = 
.
Задача 2.3. В трех хранилищах горючего хранится 175, 125 и 140 тонн бензина. Этот бензин запрашивают четыре заправочные станции в количествах, равных соответственно 180, 110, 60 и 40 тонн. Тарифы перевозок 1 тонны бензина с хранилищ к заправочным станциям заданы в таблице
| Хранилища | Заправочные станции | ||
| I | II | III | IV |
| А | |||
| В | |||
| С |
Составить такой план перевозки бензина, при котором общая стоимость перевозок является минимальной, а все заправочные станции получают столько, сколько запрашивают. Штрафы за недопоставку и за невывоз бензина равны нулю.
Ответ: Fmin=1675 при X * = 
.
Задача 2.4.На трех мелькомбинатах объединения «Мука» ежедневно производится 110, 190 и 90 тонн муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 тонн. Тарифы перевозок 1 тонны муки с мелькомбинатов к каждому из хлебозаводов известны и задаются матрицей
| Мелькомбинаты | Хлебозаводы | ||
| I | II | III | IV |
| А | |||
| В | |||
| С |
Составить такой оптимальный план доставки муки, при котором общая стоимость перевозок является минимальной.
Ответ:Fmin=1280 при X * = 
.
Задача 2.5. Заводы автомобильной фирмы MG расположены в Лос-Анджелесе, Детройте и Новом Орлеане. Основные центры распределения продукции сосредоточены в Денвере и Майами. Объемы производства указанных трех заводов равняются 1000, 1500 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимость перевозки по железной дороге одного автомобиля на одну милю равняется 8 центам. Расстояние в милях между заводами и центрами распределения приведены в таблице:
| Лос-Анджелес | |
| Детройт | |
| Новый Орлеан | |
| Денвер | Майами |
Составить такой план перевозок автомобилей в центры распределения, при котором общая стоимость перевозок является минимальной. Чему она равна? Ответ: Fmin=31320000 при X * = 
.
Задача 2.6.Заводы фирмы расположены в городах Лидсе и Кардиффе; они доставляют товары на склады городов Манчестер, Бирмингем и Лондон. Расстояния (в милях) между этими городами приведены в таблице:
| Заводы | Склады | |
| Манчестер | Бирмингем | Лондон |
| Лидс | ||
| Кардифф |
Завод в Лидсе выпускает в год 800 т. товаров, а в Кардиффе — 500 т. Манчестерский склад вмещает 400 т., Бирмингемский — 600 т., а Лондонский — 300 т. Стоимости перевозки единицы товара на единицу расстояния равны по любым направлениям. Как следует транспортировать товары для минимизации стоимости перевозок?
Ответ:Fmin=125000 при 
.
ДОМАШНЕЕ ЗАДАНИЕ
Часы суток
Требуется составить оптимальный план выпуска автобусов на смену с тем, чтобы суммарное число автобусов, работающих в сутки, было бы минимально.
Решение. Обозначим : 
число автобусов, выходящих на линию в 0 часов; 
число автобусов, выходящих на линию в 4 часа; 
число автобусов, выходящих на линию в 8 часов; 
число автобусов, выходящих на линию в 12 часов; 
число автобусов, выходящих на линию в 16 часов; 
число автобусов, выходящих на линию в 20 часов. Тогда математическая формулировка задачи принимает вид задачи линейного программирования:
Ответ: fmin=26 при 
(4; 10; 0; 8; 4; 0).
ЗАНЯТИЕ 3
ЗАДАЧА ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИЙ ПО ПРОЕКТАМ
Словесная формулировка.Имеется ряд проектов, намеченных к реализации в течение некоторого периода. По каждому проекту задан график возврата средств, выделяемых на его реализацию, представленный в виде последовательности коэффициентов возврата, выражающих собой долю взятого кредита, которую необходимо вернуть кредитору в указанное время. Требуется найти распределение средств по проектам, приносящее максимальный доход за инвестиционный период. Для решения таких задач используются линейные динамические модели.
Формальная постановка.Пусть инвестиционный период разбит на m временных интервалов, следующих непосредственно один за другим; 
и 
– объем инвестиций в j-й проект и их предельное значение соответственно; 
коэффициент возврата этих инвестиций в начале i-го интервала. Пусть средства инвестора хранятся в банке с коэффициентом доходности ki за i-й интервал. Тогда остатки 
и 
на банковском счете инвестора в начале и конце i-го периода будут равны:
; 
; 
, 
, (1.1)
где H – величина средств инвестора в начале инвестиционного периода.
Остатки на начало m-го интервала следует максимизировать:
. (1.2)
Соотношение (1.1) вместе с рекуррентными соотношениями (1.2), описывающими динамику изменения средств инвестора, условиями 
и 
, представляют формальную постановку задачи.
Задача 1.1. Компания, желая оптимальным образом использовать имеющиеся у нее денежные средства, разрабатывает оптимальный план инвестиций на ближайшие пять лет. На выбор у компании имеется пять инвестиционных проектов, параметры денежных потоков которых представлены в следующей таблице
| Год | Проект А | Проект В | Проект С | Проект D | Проект Е |
| -1 | -1 | -1 | -1 | ||
| 0,7 | -1 | 0,2 | -1 | ||
| 0,1 | 0,1 | 0,6 | 0,5 | 0,1 | |
| 0,1 | 0,1 | 0,4 | 0,9 | 0,6 | |
| 1,6 | 1,6 | 2,5 | 1,6 |
Участие в инвестиционном проекте «С» обязательное и требует не менее 6,9 млрд. руб., а проект «В» не допускает инвестиций более 6,2 млрд. руб. Размер имеющихся у компании денежных средств на момент планирования инвестиций составляет 14 млрд. руб.
Определить размеры инвестиций в каждый проект, обеспечивающие максимальную отдачу.
Решение. В соответствиис формализацией (1.1)-(1.2) остатки и на банковском счете инвестора в начале и конце i-го года будут равны:
; ; 
, 
,
Остатки в конце периода следует максимизировать:
Добавляя условия , 
, 
, получаем и решаем задачу с помощью надстройки «Поиск решения» Excel:
1) отводим блок ячеек под искомые размеры инвестиций (ячейки B10:F10 на шаблоне, рис.1 ниже);
2) считаем обороты (G3:G7) и остатки денег (H3:H7) на р/с компании для каждого года;
3) ставим задачу в «Поиске решения» и решаем ее.
Рис 1. Шаблон с решением задачи 1.1
Задача 1.2.Представители пяти проектов конкурируют между собой за получение кредита. Графики потока платежей погашения кредитов представлены в таблице:
| Год | Проекты | |||
| A | B | C | D | E |
| -1,0 | -1,0 | -1,0 | ||
| +0,3 | -1,0 | +1,0 | ||
| +1,0 | +0,3 | -1,0 | ||
| +1,0 | +1,75 | +1,4 |
Например, проект А стартует в начале первого года сразу после получения кредита; в начале второго года возвращает инвестору 0,3 от всей взятой суммы; в начале третьего года (момент окончания проекта) взятые деньги возвращаются с коэффициентом 1. Проект В аналогичен проекту А, но начинается на год позже. И так далее. Доходы, полученные от текущих проектов, можно направить в другие. Средства инвестора хранятся на банковском счете с доходностью 6% годовых. Максимальная сумма, требуемая для проекта А, равна 500 у.е. По другим проектам объем вложений не ограничен. В начальный момент у инвестора имеется 1000 у.е. Найти оптимальные объемы инвестиций в проекты, обеспечивающие максимальный доход инвестора к началу 4-го года периода.
Решение.В соответствиис формализацией (1.1)-(1.2) остатки и на банковском счете инвестора в начале и конце i-го года будут равны:
; ; 
, 
,
Остатки на начало 4-го года периода следует максимизировать:
Добавляя условия , 
; получаем задачу и решаем ее с помощью надстройки «Поиск решения» Excel:
 |  |
Рис. 1.2. Шаблон с решением задачи 1.2
Задачи для самостоятельного решения
Задача 1.3.Инвестор, располагающий суммой в 500 тыс. евро, желает максимизировать денежную наличность к концу шестимесячного периода. Характеристики возможных инвестиций даны в таблице.
| Инвестиции | Начало | Длительность | Процент дохода |
| А | каждый месяц | 1 месяц | 1,5 |
| В | месяц 1, 3, 5 | 2 месяца | 3,5 |
| С | месяц 1, 4 | 3 месяца | |
| D | месяц 1 | 6 месяцев |
Доход по каждому виду инвестиций в конце срока с процентами, указанными в таблице. С начала 5-го месяца до начала 7-го инвестору необходимо иметь на руках не менее 300 тыс. евро. Каков максимальный доход к концу шестимесячного периода?
Ответ:48499,5 евро.
Задача 1.4.Инвестор, располагающий суммой в 500 тыс. евро, желает максимизировать денежную наличность к началу 4-го года периода. Имеется таблица с коэффициентами возврата по каждому из пяти возможных вариантов инвестиций:
| Годы | Возможные инвестиции | |||
| A | B | C | D | E |
| -1,0 | -0,5 | -1,0 | -0,5 | |
| +0,3 | -0,5 | +1,0 | -0,25 | -0,5 |
| +1,0 | +0,3 | +0,1 | -0,25 | -0,5 |
| +1,0 | +1,75 | +1,4 |
Определить оптимальный план инвестиций. Чему будет при этом равен инвестиционный доход D?
Ответ: 
.
D=459039,5 евро.
Задача 1.5.Инвестор, располагающий суммой в 500 тыс. евро, желает максимизировать денежную наличность к началу 4-го года периода. Имеется таблица с коэффициентами возврата по каждому из пяти возможных вариантов инвестиций:
| Годы | Возможные инвестиции | |||
| A | B | C | D | E |
| -1,0 | -0,5 | -1,0 | -0,5 | |
| +0,3 | -0,5 | +1,0 | -0,25 | -0,5 |
| +1,0 | +0,3 | +0,1 | -0,25 | -0,5 |
| +0,2 | +1,0 | +0,3 | +1,75 | +1,4 |
С учетом рисков на каждый из вариантов решено направить не менее 100 тыс.евро. Чему будет при этом равен инвестиционный доход при оптимальном инвестировании?
Ответ:D=465666,7 евро.
ТРАНСПОРТНАЯ ЗАДАЧА
Словесная формулировка. Имеется поставщиков А1, А2 , … , Аm некоторого однородного грузас запасами a1, a2,…,am соответственно. Имеется потребителей B1, B2,… , Bn этого груза c заявками b1, b2,…,bn. Заданы тарифы перевозок , означающие стоимости перевозки единицы груза от Ai к Bj ; кроме того, заданы штрафные тарифы , означающие издержки, вызываемые каждой единицей невывезенного груза поставщиков , , а также штрафные тарифы , означающие издержки, вызываемые каждой единицей недопоставленного груза потребителям , . Требуется составить такой план перевозки грузов, при котором: 1) объемы вывозимых грузов не превышают запасы поставщиков; 2) объемы поставок не превышают заявки потребителей; 3) суммарные издержки всех перевозок минимальны.
Формальная постановка. Используя введенные обозначения, имеем:
(2.1)
(2.2)
Задача 2.1.Имеется пять поставщиков и пять потребителей некоторого груза. Стоимости перевозки единицы груза сij от i-го поставщика к j-му потребителю, данные о возможностях поставщиков и запросах потребителей, а также штрафы за недопоставку/невывоз каждой единицы груза, представлены в следующих таблицах:
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | Потребитель 5 | Штрафы за невывоз |
| Поставщик 1 | |||||
| Поставщик 2 | |||||
| Поставщик 3 | |||||
| Поставщик 4 | |||||
| Поставщик 5 |
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | Потребитель 5 |
| Штрафы за недопоставку |
| Поставщик 1 | Поставщик 2 | Поставщик 3 | Поставщик 4 | Поставщик 5 |
| Возможности поставщиков |
| Потребитель 1 | Потребитель 2 | Потребитель 3 | Потребитель 4 | Потребитель 5 |
| Запросы потребителей |
Каждый поставщик заинтересован поставить весь имеющийся у него груз, каждый потребитель – максимально удовлетворить свои потребности. Составить оптимальный план перевозок с минимальной стоимостью.
Решение: 1) переписываем «возможности поставщиков» в столбец как «запасы»;
2) переписываем «запросы потребителей» как «потребности»
3) подсчитываем (в ячейках В9 и I2) суммарные запасы и суммарные потребности, определяя после этого тип задачи (закрытая, на избыток или на недостаток);
4) подсчитываем кол-во вывезенного (В18:В22), привезенного (D16:H16) груза, остатки у поставщиков (J18:J22) и недопоставки у потребителей (D24:H24);
5) подсчитываем издержки (B13; D13; F13; H13); 7) вызываем «Поиск решения» и решаем задачу:
Рис 2.1. Шаблон с решением задачи 2.1
Задачи для самостоятельного решения
Задача 2.2. Для строительства 4-х объектов используется кирпич, изготовляемый на трех заводах. Ежедневно на заводе1, заводе2 и заводе3 может изготовляться соответственно 100, 150 и 50 тыс. шт. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов равны 75, 80, 60 и 85 тыс. шт. Известны также тарифы перевозок 1 тыс. шт. кирпича с каждого завода к каждому из строящихся объектов:
| Объект1 | Объект2 | Объект3 | Объект4 |
| Завод1 | |||
| Завод2 | |||
| Завод3 |
Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок является минимальной. Чему она равна? Ответ: Fmin=665 при X * = .
Задача 2.3. В трех хранилищах горючего хранится 175, 125 и 140 тонн бензина. Этот бензин запрашивают четыре заправочные станции в количествах, равных соответственно 180, 110, 60 и 40 тонн. Тарифы перевозок 1 тонны бензина с хранилищ к заправочным станциям заданы в таблице
| Хранилища | Заправочные станции | ||
| I | II | III | IV |
| А | |||
| В | |||
| С |
Составить такой план перевозки бензина, при котором общая стоимость перевозок является минимальной, а все заправочные станции получают столько, сколько запрашивают. Штрафы за недопоставку и за невывоз бензина равны нулю.
Ответ: Fmin=1675 при X * = .
Задача 2.4.На трех мелькомбинатах объединения «Мука» ежедневно производится 110, 190 и 90 тонн муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 тонн. Тарифы перевозок 1 тонны муки с мелькомбинатов к каждому из хлебозаводов известны и задаются матрицей
| Мелькомбинаты | Хлебозаводы | ||
| I | II | III | IV |
| А | |||
| В | |||
| С |
Составить такой оптимальный план доставки муки, при котором общая стоимость перевозок является минимальной.
Ответ:Fmin=1280 при X * = .
Задача 2.5. Заводы автомобильной фирмы MG расположены в Лос-Анджелесе, Детройте и Новом Орлеане. Основные центры распределения продукции сосредоточены в Денвере и Майами. Объемы производства указанных трех заводов равняются 1000, 1500 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимость перевозки по железной дороге одного автомобиля на одну милю равняется 8 центам. Расстояние в милях между заводами и центрами распределения приведены в таблице:
| Лос-Анджелес | |
| Детройт | |
| Новый Орлеан | |
| Денвер | Майами |
Составить такой план перевозок автомобилей в центры распределения, при котором общая стоимость перевозок является минимальной. Чему она равна? Ответ: Fmin=31320000 при X * = .
Задача 2.6.Заводы фирмы расположены в городах Лидсе и Кардиффе; они доставляют товары на склады городов Манчестер, Бирмингем и Лондон. Расстояния (в милях) между этими городами приведены в таблице:
| Заводы | Склады | |
| Манчестер | Бирмингем | Лондон |
| Лидс | ||
| Кардифф |
Завод в Лидсе выпускает в год 800 т. товаров, а в Кардиффе — 500 т. Манчестерский склад вмещает 400 т., Бирмингемский — 600 т., а Лондонский — 300 т. Стоимости перевозки единицы товара на единицу расстояния равны по любым направлениям. Как следует транспортировать товары для минимизации стоимости перевозок?
Ответ:Fmin=125000 при .
Источник