Задача определить ежегодную доходность купонной облигации

Ориентиром доходности облигаций служит номинальная (нарицательная) цена бумаги, фиксируемая на бланке.

Р_н — номинальная цена бумаги,

З — сумма займа, приходящаяся на все долговые обязательства определенного достоинства

К — кол-во эмитируемых бумаг определенного достоинства.

Облигации эмитируются, как правило, с высокой номинальной ценой и ориентированы либо на богатых инвесторов, либо на институциональных инвесторов. Лица с относительно невысокими доходами могут приобрести облигации через инвестируемые фонды.

Эмиссионная цена— это цена первичного размещения. Она может быть больше, меньше, равной номинальной. Если эмиссионная цена меньше номинальной, то цена оказывается дисконтной или со скидкой. Если эмиссионная цена больше номинальной, то цена называется с премией.

Рыночная (курсовая) цена — это цена, по которой облигация продаётся на вторичном рынке. Отношение рыночной цены ( Р_р) к номинальной (Р_н), выраженной в %-тах называется курсом.

Доходность облигаций определяется двумя факторами:

1. вознаграждение за предоставляемый эмитенту заём — купонные выплаты,

2. разница между ценой по гашения и ценой приобретения ц.б.

1. Купонные выплаты выражаются абсолютной величиной или в %-тах:

I_к — купонный доход,

iд — купонная годовая %ая ставка.

Облигация может быть реализована не в начале фин-ого года. Тогда купонный доход будет делиться между прежним и новым владельцем.

t₁ — число дней от даты продажи до очередного %-ого дня (даты выплаты по купону),

t₂ — число дней от прошедшего процентного дня до даты продажи.

На основании годового купонного дохода определяется купонная (текущая) доходность — ставка текущего дохода.

Р_пр — цена приобретения облигации

2. Разница между ценой приобретения погашения бумаги определяет величину прироста или убытка капитала за весь срок займа .

ДельтаР = Р_н — Р_д, ДельтаР›0 (прирост капитала)

ДельтаР = Р_н -Р_премия, ДельтаР‹0 (убыток капитала)

Р_д — цена со скидкой (дисконтом)

Р_премия — цена с премией

n -число лет займа

Годовой совокупный доход

Совокупная доходность (ставка совокупного дохода, ставка помещения)

Совокупный доход за весь срок займа

Совокупная доходность за весь срок займа

1 Облигация приобретена по курсовой цене 1200 рублей, погашается через 5 лет по номиналу 1000 рублей. Купонная ставка равна 8%. Определить ставку помещения по данной бумаге.

1000-1200 = -200 (убыток капитала)

-200/5 = — 40 (годовой убыток капитала)

0,08*1000 = 80 (купонный доход)

(80+ (-40))/1200 = 0,033 или 3,3% (ставка помещения)

2 Облигация приобретена по курсовой цене 1300 рублей. Погашается через 3 года по номиналу 1000 рублей. Купонная ставка 20%. Определить ставку совокупного дохода по облигации за весь срок займа.

0,2*1000=200 (купонный доход)

(1000-1300)/3 =-100 (годовой убыток капитала)

(200-100) *3/1300 = 0,2308 или 23,08% (ставка помещения)

3. Облигация с номиналом 1000 рублей с 5%-ой купонной ставкой и погашением через 5 лет приобретена с дисконтом 10%. Определить текущую и совокупную доходность бумаги за год и за 5 лет.

1000*0,05 = 50 (купонный доход)

(1000-1000*(1-0,1))/5 = 20 (годовой прирост капитала)

(50+20)/900 = 0,078 (совокупная годовая доходность)

0,078*5 = 0,39 (совокупная доходность за 5 лет)

4. Облигация номиналом 10000 рублей и сроком займа 5 лет с ежегодной выплатой 50% приобретена с премией за 14000 рублей. В 1-ый, 2-ой, 3-ий, 4-ый и 5-ый год после эмиссии. Погашение проводится по номиналу. Определить годовой убыток капитала, годовой совокупный доход, годовую совокупную доходность для разных сроков приобретения облигаций.

(10000-14000)/5 = -800 (годовой убыток капитала для 5 лет)

(10000-14000)/4 = -1000 (годовой убыток капитала для 4 лет)…

Источник

Билет 1

Номинал бескупонной облигации равен 1000 р., бумага погашается через 5 лет. Определить цену облигации, если ее доходность до погашения должна составить 12% годовых .

Билет 2

Номинал бескупонной облигации равен 1000 р., бумага погашается через 30 дней. Определить цену облигации, если ее доходность до погашения должна составить 4% годовых . База 365 дней.

P = N /( 1+( rt /база)) = 1000/(1+( 0,04*30/365)) = 997р.

Билет 3

Номинал бескупонной облигации равен 1000 р., бумага погашается через 3 года. Облигация стоит 850 руб. Определить доходность до погашения облигации.

Билет 4

Номинал бескупонной облигации равен 1000 р., купон 3.5%. Облигация стоит 1005 руб. Определить текущую доходность облигации.

Билет 5

Номинал облигации 1000 руб., купон 9% выплачивается два раза в год. До погашения облигации 4 года. Облигация стоит 1040 руб. Определить ее доходность до погашения

r =( ( N — P )/ n + C )/(( N + P )/2) = ((1000-1040)/4+90)/((1000+1040)/2) = 0,078 (7,8%)

Билет 6

Номинал краткосрочной бескупонной акции 1000р., цена 950р. Облигация погашается через 200 дней. Определить доходность до погашения облигации. База 365 дней.

R=(N/P-1)* база /t = ( 1000/950 – 1)*365/200 = 0,096 (9,6%)

Билет 7

Инвестор планирует купить акцию компании А и продать ее через год. Он полагает, что к моменту продажи курс акции составить 120р. К этому моменту по акции будет выплачен дивиденд в размере 5р. Определить цену акции если доходность от вложения бумаги должна составить 25%.

Билет 8

Инвестор планирует купить акцию компании А и продать ее через год. Он полагает, что к моменту продажи курс акции составить 120р. За год по акции не будут выплачиваться дивиденды. Определить цену акции если доходность от вложения бумаги должна составить 25%.

Билет 9

Номинал облигации равен 1000 руб., купон 7%, выплачивается один раз в год. До погашения облигации 5 лет. Облигация стоит 890 р. Определить ориентировочную доходность до погашения облигации.

Билет 10

На акции компании А был выплачен дивиденд 10 р. На акцию Инвестор полагает, что в течение последующих лет темп прироста дивиденда составит 6% в год. Доходность равная риску покупки акции равна 25%. Определить цену акции.

Билет 11

Курс акции компании А составляет 45 руб., доходность, равная риску инвестирования в акцию 15%. На акцию выплачен дивиденд 2 руб. Определить темп прироста будущих дивидендов, если он предполагается постоянным.

P=div(1+g)/(r-g) Pr-Pg=div-divg Pr-div= Pg+ divg; Pr-div= g(P+div); g= Pr-div/( P+div) = 45*0,15-2/(45+2) = 0,101 (10,1%)

Билет 12

Определить цену привилегированной акции, если по ней выплачивается фиксированный дивиденд 10 руб. Ставка дисконтирования, соответствующая риску инвестирования в акцию, равна 15%.

Билет 13

Инвестор купил акцию за 100 руб. и продал через три года за 200 руб. В конце первого года ему выплатили дивиденд в размере 10 руб., за второй – 12 руб., за третий – 14 руб. Определить ориентировочно доходность операции вкладчика.

Билет 14

Инвестор купил акцию за 80 руб. и продал через 90 дней за 120 руб. За это время на акцию был выплачен дивиденд 4 руб. Определить доходность операции вкладчика.

r=((Ps-Pb+div)/Pb)*(365/t) = ((120-90+4)/80)*( 365/90) = 223%

Билет 15

Инвестор купил акцию компании А по цене 20 руб. и продал ее через три года за 60 руб. за это время дивиденды на акцию не выплачивались. Определить доходность операции инвестора в расчете на год.

Билет 16

Фондовый индекс состоит из акций трех компаний А , В и С. Индекс рассчитывается как простое среднее арифметическое. Цены акций равны: А – 20 руб., В – 35 руб., С – 50 руб. На следующий день происходит дробление акции С в пропорции 1:2. определить новое значение делителя индекса.

Билет 17

Фондовый индекс состоит из акций трех компаний А В С. Индекс рассчитывается как простое среднее арифметическое. Цены А-20 В-35 С-30. Делитель индекса 2,2857

На след. День изменяется состав индекса. Исключают А Включают Е – 40 рублей. Определить новое значение индекса.

Билет 18

Фондовый индекс состоит из акций трех компаний А В С. Индекс рассчитывается как среднее арифметическое взвешенное по капитал . к омпании. На момент начала расчета индекса А – 15р Количество 100, В – 20р Количество 200, С – 40р Количество 350

В момент t цена акций составила А – 25, В – 30, С – 50. Определить значение инд. в момент времени t и охарактеризовать рост на основе значения.

I=(15100+20200+40*350)/(100+200+350) = 30

Фондовый индекс состоит из акций трех компаний А В С. Индекс рассчитывается как среднее арифметическое взвешенное по капитал. компании .Н а момент начала расчета индекса А – 25р Количество 200, В – 30р Количество 300, С – 55р Количество 400

В момент t цена акций составила А – 32, В – 45, С – 44. Значение индекса в момент расчета 10. Определить значение индекса в момент времени t.

Рост = (It /I)*10= 10,42

Билет 20

Вкладчик разместил в банке 75000 рублей под 9% годовых. Какую сумму он получит через 2 года при начислении сложного процента раз в квартал.

Билет 21

Вкладчик рассчитывает накопить на вкладе 500 тыс рублей через 3 года.

Банк начисляет 12% годовых раз в квартал. Какую сумму он должен положить сегодня в этом банке.

P = Pn /( 1+ r / m ) mn = 500000/( 1+0,12/4) 12 = 350689р.

Билет 22

Вкладчик инвестировал 10000 р и получил через пять лет 50 000 рублей. Процент начислялся ежеквартально. Определить доходность операции в расчете на год.

Билет 23

Инвестор разместил деньги на 6 лет. Капитализация процентов осуществлялась ежедневно. Какую ставку начислял банк, если в конце периода капитал вкладчика увеличился в 4 раза.

Билет 24

r=((Ps-Pb+div)/Pb)*(365/t) = ((120-90+4)/80)*( 365/90) = 223%

Билет 25

Акционер владеет 100 акциями компании А. Номинал равен 150 рублей, рыночная стоимость 350 рублей. Дробление акций 1 к 3.

А) какое кол-ва акций будет иметь акционер после дробления

Б) Величина номинала и примерной рыночной стоимости после дробления

A) после дробления 1/3 300 акций

Б) номинал 150*1/3 = 50р, рын ст-мость 350*1/3 = 116,7 р

Билет 26

Номинал облигации 1000 рублей, купон 10%, выплачивается 1 раз в год. До погашения 3 года. Определить цену облигации если ее доходность должна составить 12%.

Билет 27

Номинал облигации 1000 рублей, купон 10%, выплачивается 2 раза в год. До погашения 2 года. Определить цену облигации если ее доходность должна составить 8%.

P= C/r +( N-C/r)*(1/(1+r/m) mn ) = 100/0,08+(1000-100/0,08)*(1/(1+0,08/2) 4 )=1036 р.

Источник

Пример решения задачи

Облигация номиналом 1000 руб. с купонной ставкой 12% выпускается на три года, купонные выплаты − два раза в год, требуемая норма доходности (альтернативная ставка доходности) − 15%. Определить текущую стоимость.

;

Ответ: 929,59 руб.

При торговле на рынке облигаций обычно указывается не цена (в денежных единицах), а курс – отношение цены к номиналув процентах.

Курс облигации – процентное выражение цены облигации, отношение ее цены к номиналу.

Например, курс приведенной в табл. 11.3 облигации «Силовые машины» 17.01.2015 г. составил 93,857. При номинале в 1000 руб. цена составляет 938,57 руб.

Следует, впрочем, иметь в виду, что часто, применительно к облигациям, говоря «цена» подразумевают именно курс, так как во всех информационных и торговых системах котировки указываются именно в процентах от номинала.

На некоторых рынках (например, США) курс устанавливается с использованием не десятичной, а простой дроби (в 32 долях). Поэтому для нахождения курса облигации необходимо перевести дробь в десятичную.

Различают «чистую» и «грязную» цену облигации.

Именно «чистая» цена приводится на терминалах информационных агентств, в сводках газет и прочих СМИ, где публикуется финансовая информация. «Чистая» цена рассчитывается исходя из того, что проценты по ней будут выплачены в полном объеме владельцу облигации на момент выплаты процентного дохода. Представим ситуацию, когда продажа облигации произведена ровно между выплатами купонного годового дохода. В этом случае очередной купонный платеж получит покупатель облигации. Продавец должен компенсировать себе неполученные проценты за полгода, продав ее не по «чистой» цене, а за иную сумму, равную «чистой» цене, плюс величине накопленных за этот период процентов. Это и будет «грязная»цена облигации.

«Грязная» цена облигации = «чистая» цена + накопленный купонный доход

На рынке облигации котируются по «чистой» цене, а сделки совершаются по «грязной» цене. В табл.10.4 приведены данные о накопленном купонном доходе (НКД), которые используются для определения «грязной» цены. Для иллюстрации рассмотрим пример облигации Абсолют-банка. К чистой цене (922,9 руб) надо прибавить НКД (18,74 руб) = 941,64. Курс (в процентах от номинала) равен 94,164.

Доходность облигаций

Помимо цены (курса) облигации важнейшим показателем является доходность (норма доходности).

Существует несколько показателей доходности:

· Номинальная доходность

Номинальная доходность (ставка купона) – отношение суммы купона к номиналу:

· Текущая доходность

Текущая доходность – отношение суммы купона к текущей стоимости облигации: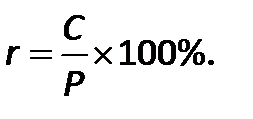

· Доходность к погашению

Доходность к погашению(внутренняя доходность облигации)– эффективность инвестиции, доходность, которая будет получена при удержании облигации до погашения.

· Полная доходность

Конечная,или полная, доходность характеризует полный доход по облигации, приходящийся на единицу затрат на покупку этой облигации в расчете на год. Схожа с предыдущим показателем. Разница в том, что в данном случае инвестор не держит облигацию до погашения.

Обычно в СМИ приводится показатель доходности до погашения(англ. Yield to Maturity, YTM).Синоним – IRR, internal rate of return, внутренняя доходность финансового инструмента/потока платежей. Под внутренней доходностью финансового инструмента называют доходность (ставку дисконтирования), при которой приведенная стоимость потока платежей финансового инструмента равна его рыночной цене.

Смысл показателя «доходность до погашения» заключается в том, что он позволяет оценить эффективность инвестиций в облигации не только по такому параметру, как купонная ставка, но и с учетом разницы цены облигации при покупке и ценой ее погашения.

Если взять купонную облигацию, то формула расчета доходности до погашения вытекает из вышеприведенной формулы ее цены. Иными словами, надо найти r (требуемую норму доходности). Задача решается методом итерации, что связано с достаточно долгими вычислениями. Если возникает подобная задача на профессиональном уровне, она решается с помощью финансовых калькуляторов, компьютерных программ или специальных таблиц (вроде математических таблиц Брадиса), которыми активно пользовались (да и сейчас продолжают пользоваться) до появления современных средств вычислительной техники.

Когда же под рукой нет ни того, ни другого, можно рассчитать приблизительную доходность до погашения, используя следующую формулу:

.

В предыдущей задаче с ценой облигации представим себе, что нам известна ее текущая цена ($1166,52), но неизвестна доходность r.

Примерное значение .

Поскольку мы знаем истинное значение r (4%), мы может оценить, насколько сильно наша грубая оценка отличается от точной.

Дюрация облигаций

Как было показано выше, изменение процентных ставок на рынке при прочих равных условиях – основной фактор, влияющий на цену/курс облигаций. При этом разные облигации (срок до погашения, купонная ставка) по-разному реагируют на изменения рыночных процентных ставок.

В 1930‑е гг. был разработан показатель, определяющий чувствительность цены облигаций к изменению процентной ставки. Он получил название «дюрация».

Дюрация (англ. duration – длительность) – это средневзвешенный срок потока платежей, взвешенный по дисконтированной сумме. Иными словами – это точка равновесия сроков дисконтированных платежей.

Дюрация является важнейшей аналитической характеристикой облигации.

Само понятие дюрации было введено американцем Ф. Маколи и (независимо) англичанином Дж. Хиксом [83] . Часто в литературе пишут «дюрация Маколи(ея)»

,

где C – купонный платеж по облигации;

n – период поступления i-го дохода;

PV – приведенная (дисконтированная) цена облигации;

r – доходность к погашению.

С одной стороны, дюрация представляет собой показатель эластичности цены облигации по процентной ставке и характеризует риск изменения цены облигации при изменении процентной ставки. С другой стороны, это средневзвешенное время до погашения купонов и номинала облигации. Обычно измеряется в годах или днях (в России − в днях, см. табл. 10.4).

Предположим, что срок обращения облигации составляет три года, купонная ставка 9%, эффективная доходность – 10% годовых, номинал облигации 1000 руб., ее приведенная стоимость 975,1 руб. Тогда дюрация такой бумаги будет равна:

Источник

Задача определить ежегодную доходность купонной облигации