Теория В. Шарпа
Теория В. Шарпа – теория соотношения риска и дохода от инвестиций в ценные бумаги.
Основные принципы теории В. Шарпа
Теорию соотношения риска и дохода от инвестиций в ценные бумаги в 1960-х годах развивает Уильям Шарп. Он вводит в научный обиход несколько важных категорий. Во-первых, Шарп разделил общий риск инвестиций в ценные бумаги на две части: риск систематический и риск несистематический. Во-вторых, он разработал Модель оценки капитальных активов (Мока) (Capital Asset Pricing Model – CAPM). Систематическим он назвал риск, связанный с состоянием рынка. В свою очередь, последний зависит от изменений в экономике и финансах страны, а также от изменений в мировой торговле, международном движении капиталов, состоянии валют. Риск, связанный с системой экономических и финансовых отношений, нельзя преодолеть с помощью диверсификации портфеля, предложил Г. Марковиц. Систематический риск в экономической литературе называют также недиверсифицированным, или рыночным, и обозначается он буквой β – бета. Несистематический риск еще называется диверсифицированый, или портфельный. Его природа отличается от природы риска систематического. Инвестор может преодолеть несистематический риск посредством диверсификации портфеля. С этой целью он должен изучать финансовое состояние эмитентов ценных бумаг. Фундаментальный анализ финансового состояния эмитента направлен на выяснение возможностей банкротства, дефолта, потери капитала и других неблагоприятных ситуаций, которые могут возникнуть у эмитента. Инвесторы стремятся подобрать такой «ассортимент» ценных бумаг, в котором риск и доходность сбалансированы. В. Шарп объясняет причину разделения общего риска на две части различным влиянием этих частей на ожидаемую доходность. Ценная бумага с высокой степенью систематического риска, то есть с высшим бетой, может принести инвестору выше ожидаемый доход. Несистематический риск с бетой не связан, поэтому увеличение собственного, то есть диверсифицированного, риска не ведет к росту ожидаемой доходности. Инвесторы вознаграждаются только рыночного, то есть систематический риск, несистематический риск вознаграждается. Американские авторы отмечают, что в основу стратегического финансового управления должны быть положены методы управления несистематическим риском и глубокое изучение систематического риска.
Модель оценки капитальных активов
В. Шарп предложил модель оценки капитальных активов (Мока) (Capital Asset Pricing Model – CAPM), на основании которой корпорация может определить цену капитала, то есть стоимость приобретения капитала, необходимого для ведения предпринимательской деятельности. Инвестор, вкладывающий свой капитал в ценные бумаги, выпущенные корпорацией на основе, определяет его доходность с учетом риска. Модель, как и любая теоретическая концепция, основанная на абстракции, то есть на многих допущениях. Модель предусматривает совершенный, идеальный рынок ценных бумаг (perfect market), то есть: информация является одинаково доступным для всех инвесторов; все ценные бумаги, имеющие риск, обращающихся публично; налогов и операционных расходов нет; инвесторы могут давать деньги в ссуду и занимать по безрисковой процентной ставке. Особенность модели заключается в том, что она дает возможность определить связь между риском и доходностью ценной бумаги. Портфель состоит из множества ценных бумаг, каждый из них вносит свою долю в определенный риск и ожидаемый доход. Поэтому возникла необходимость определения риска и дохода каждого участника портфеля.
Выбор ценной бумаги без риска. Идея выделения ценной бумаги, не содержащей в себе риска (Risk Free Asset – Rf), принадлежит Гарри Марковицу. Стандартное отклонение по таким ценным бумагой равна нулю. Доход должен быть:
- стабильным;
- заранее и точно определенным.
Ни одна корпорация таких бумаг в условиях рыночной экономики эмитировать не сможет. Такую ценную бумагу может выпускать только государство. Облигация, эмитированная государством, приносит фиксированный доход, выплата которого гарантирована налогами, поступают в бюджет. Однако это утверждение достаточно сомнительно. Во-первых, доход по государственной облигации может быть обесценен инфляцией. Во-вторых, были неоднократные случаи отказа государства от своих долгов, их пролонгации, снижение процентных ставок. Гарри Марковиц считает, что каждую государственную облигацию можно считать безрисковой. По его мнению, безрисковым может быть только трехмесячный казначейский вексель товары с дисконтом. Если инвестор сохраняет его в своем портфеле три месяца, он получит доход по соответствующей процентной ставке. У. Шарп пришел к выводу, что практически безрисковых ценных бумаг в США нет, все государственные ценные бумаги являются рисковыми с точки зрения получения реального дохода. Введение в модель безрискового дохода является абстракцией, теоретической условностью, которая необходима как отправная точка отсчета, как определенная база для определения ожидаемого дохода по ценной бумаге.
Ставка дохода рыночного портфеля и премия за риск
Рыночным называется портфель (market portfolio), состоящий из всех ценных бумаг, обращающихся на рынке капиталов. При этом доля (удельный вес) каждой ценной бумаги соответствующей его доле в общей капитализации рынка. Средняя ставка дохода рыночного портфеля используется в модели оценки капитальных активов для определения премии за риск. По определению рыночного портфеля в финансовой литературе ведутся дискуссии, многие авторы отмечают неопределенность рыночного портфеля. Ведутся дискуссии о том, какие активы следует включать в рыночный портфель. Нужно ли включать в него государственные ценные бумаги, золото, имущество, принадлежащее населению, вложения в образование – так называемый человеческий капитал и др. На практике в рыночный портфель включаются ценные бумаги, на основании которых составляются всемирно известные индексы, например индекс корпорации Стэндард энд Пурьз. Менеджеры инвестиционных фондов или других инвестиционных институтов определяют портфели для каждого класса активов. На рынке капиталов происходит специализация инвесторов не только по классам ценных бумаг (акции или облигации), но и внутри классов. Производится так называемый инвестиционный стиль. Это означает, что инвестор формирует портфель из определенных ценных бумаг, например, только по ценным бумагам, которые эмитируются финансовыми корпорациями, или акций с высокими дивидендами и капитализацией.
Источник
Модель У. Шарпа как альтернатива модели Марковица
Добрый день, уважаемое сообщество трейдеров, инвесторов и всех кто интересуется рынком ценных бумаг!
Модель У. Шарпа или как её ещё называют часто рыночная модель была впервые предложена американским экономистом, лауреатом Нобелевской премии Уильямом Форсайтом Шарпом в середине 60-х годов прошлого столетия.

Уильям Ф. Шарп является в настоящее время почетным профессором Высшей школы бизнеса Стэнфордского университета.
В 1990 г. он получил Нобелевскую премию по экономике, которую он получил за развитие теории оценки финансовых активов.
Он является одним из трех авторов одного из самых популярных в мире фундаментального учебника по курсу «ИНВЕСТИЦИИ«.
В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Предполагается, что доходность обыкновенной акции за определенный период связанна с доходностью за аналогичный период с доходностью рыночного индекса. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции и наоборот.
Таким образом данная модель предполагается линейной. А уравнение предложенной модели имеет следующий вид:
Главное отличие модели У. Шарпа от модели Г. Марковица состоит в следующем:
Модель Шарпа рассматривает взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом, в то время как модель Марковица — рассматривает взаимосвязь доходностей ценных бумаг между собой.
Именно для того, чтобы избежать высокую трудоемкость модели Марковица Уильям Шарп предложил рыночную (индексную) модель. При этом модель Шарпа это не новый метод составления портфеля ценных бумаг — это упрощенная модель Марковица, где решение проблемы выбора оптимального портфеля осуществляется с меньшими усилиями. Модель Шарпа обычно применяют при рассмотрении большого количества ценных бумаг, которые представляют значительную часть рынка.
Весьма интересным представляется сравнение результатов полученных по модели Марковица и модели Шарпа.
Для этого мной было разработано приложение, в Microsoft Office Excel*, под названием — «Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)«.
В недавнем своем посте я демонстрировал результат расчета определения оптимального расчета на российском рынке акций по модели Марковица со следующими вводными:
- были взяты акции входящие в расчет основного индекса Московской Биржи — Индекса ММВБ — 50 наиболее ликвидных и капитализированных ценных бумаг на российском рынке акций;
- исторический период для анализа по рассматриваемым инструментам был выбран с 09 января 2007 года по 24 октября 2013 года;
- уровень ожидаемой доходности — максимальный;
- уровень приемлемого риска — минимальный;
- диверсификация (максимальная доля вложений в финансовый инструмент) — 15% от имеющихся активов;
- минимальный уровень дневной ликвидности по акциям — 6 млн. рублей.
Аналогичные параметры были использованы при расчете оптимального портфеля по модели Шарпа.
Полученный результат по указанным моделям Вы можете видеть ниже:
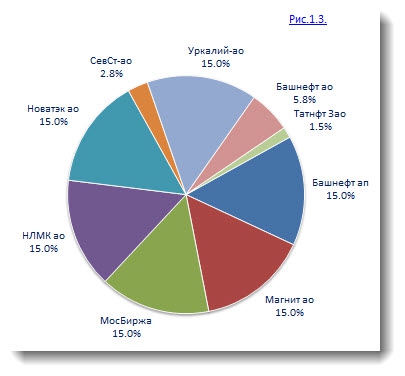
Модель Марковица:
Модель Шарпа: 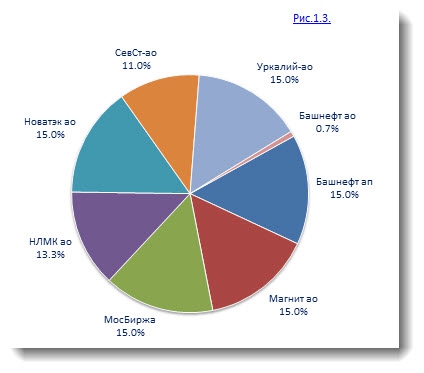
Как видно разница в составе предложенных оптимальных портфелей ценных бумаг небольшая. В модели Шарпа доля бумаг Северстали составила — 11% против 2,8% в модели Марковица; акции Башнефти в модели Шарпа менее 1%, в модели Марковица — 5,8%; в модели Шарпа акции НЛМК -13,3%, в модели Марковица — 15%; в модели Шарпа акций Татнефти нет совсем, в модели Марковица — 1,5%. Остальные доли бумаг одинаковы для описываемых моделей.
Итоговые параметры следующие:
Модель Марковица: 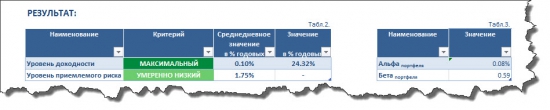
Модель Шарпа:
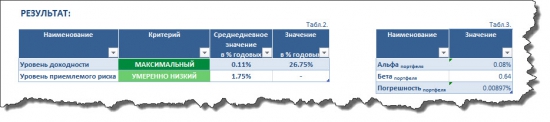
Здесь мы наблюдаем, что при одинаковом уровне риска доходность портфеля Шарпа оказывается несколько выше доходности по модели Марковица — 26,75% против 24,32% годовых, соответственно. При этом мы видим, что бета портфеля по модели Шарпа также выше беты получаемой по модели Марковица (0,64 против 0,59), а это, в свою очередь говорит о том, что портфель Шарпа является чуть менее оборонительным (защитным), чем портфель Марковица.
Рыночная модель У. Шарпа оптимального портфеля в итоге выглядит следующим образом:
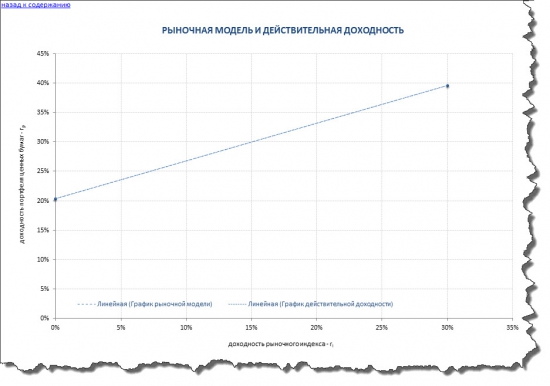
Все остальные расчетные показатели в представленном приложении «Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)» являются такими же как и в модели Марковица.
Приложение «Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)» содержит также те же технические характеристики, что и приложение «Портфельные инвестиции на российском рынке акций по модели Марковица»
В журнале сделок настроен удобный, быстрый переход от одной страницы к другой за счет внутренних гиперссылок. Гиперссылки к графикам позволят быстро перейти к нужной сводной таблице на базе которых они построены. В наличии подробная инструкция для работы с приложением .
Всего в приложении более 65 различных графиков, более 75 сводных таблиц и все четко структурированы.
Приложение настроено так, что Вы легко сможете распечатать все листы (нет необходимости специально форматировать их), чтобы делать для себя специальные папки куда вы можете подшивать Ваши расчеты и т.д. и т.п. Все страницы пронумерованы.
Также Вы сможете, при желании, преобразовать его в удобный, читаемый PDF формат (при наличии специальной программы для создания PDF файлов).
Для наглядности я выложил итоговый файл с данными, преобразованный в PDF формат, на общем диске. Вы можете пройти по ссылке и посмотреть либо скачать:
Все формулы в приложении открыты так, что Вы можете заглянуть в глубь самих расчетов в части использованных в приложении различных показателей.
При желании исходную базу данных приложения о ценовых параметрах, уже включенных в него финансовых инструментов, можно изменить, расширить (как по перечню рассматриваемых бумаг, так и по горизонту их исследования) и конечно же периодически обновлять приложение на текущую дату.
В условиях развитых и стабильно функционирующих фондовых рынков вышеупомянутые классические модели Марковица и Шарпа работают вполне эффективно. При этом в современных условиях применение лишь отдельно взятой модели не является правильным. Модели У. Шарпа и Г. Марковица могут являться хорошим дополнением к другим факторам при составлении оптимального портфеля ценных бумаг.
«Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)» — это отличный инструмент для профессионального подхода к инвестированию на рынке ценных бумаг.
Если Вас заинтересовало приложение, то его можно приобрести либо на сайте:
Либо в качестве альтернативного варианта для приобретения Вы можете обратиться ко мне письмом на адрес alexeyboyarskiy@gmail.com
Всем удачной торговли!
* Для корректной работы журнала необходима версия Excel 2010 и выше.
Источник