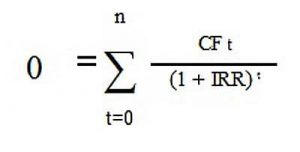Внутренняя норма окупаемости затрат

Расчет внутренней нормы доходности

Ни один инвестор не вкладывает средства слепо, не проведя предварительных исследований: он должен быть уверен, что они окупятся или, как минимум, их удастся вернуть. Для этого оценивается потенциальная рентабельность инвестиционного проекта. Конечно, это нельзя сделать иначе как комплексно, применяя ряд специально разработанных показателей, важнейший из которых – внутренняя норма доходности.

Рассмотрим, в чем особенности метода инвестиционных исследований, основанного на вычислении внутренней нормы доходности – IRR.

Что такое внутренняя норма доходности?

Никто не может рассчитать с вероятностью 100%, какой доход удастся получить от вложенных средств. Слишком много переменных факторов, могущих повлиять на реализацию бизнес-проекта, профинансированного инвестором. Однако можно максимально снизить риск неточностей, если применить не абсолютную, а относительную оценку.

Та процентная ставка, при которой инвестор гарантированно возместит свое вложение, но не получит прибыли, называется внутренней нормой доходности (ВНД). Норма заключается в том, что все денежные потоки данного инвестиционного проекта в сумме взаимозачтутся. Иначе говоря, расходы на инвестиционный проект в какой-то момент времени уравновешиваются полученными доходами (говорят, что проект «вышел в ноль»).

ВАЖНО! Слово «внутренняя» в определении данной нормы инвестиционных вложений означает ее зависимость от свойств самого проекта, а не от внешних факторов.

Внутреннюю норму доходности специалисты могут именовать по-разному. Встречаются следующие наименования:

• ВНД – русская аббревиатура;
• IRR – английская аббревиатура от «Internal Rate of Return» – «внутренняя норма доходности»;
• внутренняя норма рентабельности;
• внутренняя норма прибыли;
• внутренняя норма возврата инвестиций;
• предельная эффективность капитальных вложений;
• процентная норма прибыли;
• дисконтированный поток реальных денег;
• финансовая норма прибыли;
• собственная норма прибыли.

ВНИМАНИЕ! Эту норму можно счесть предельной, поскольку выход за ее пределы уже означает для инвестора убыток.

Показатели для расчета IRR

Математически расчет внутренней нормы доходности не так уж сложен, но формула включает много дополнительных показателей, которые необходимо учитывать. Среди них:

• NPV – от первых букв выражения «Net Present Value» («чистая приведенная стоимость») – сумма всех денежных потоков данного проекта, приведенная к общему показателю при взаимозачете доходов и затрат;
• CF – денежные потоки (от «Cash Flows») – величины различных притоков и оттоков финансов, в том числе и инвестируемых средств, в выбранный период времени t (обычно берется год). Для инвестиционного проекта первый денежный поток – сама инвестиция – естественно, будет иметь отрицательное значение (это затрата).
• R – ставка дисконтирования, то есть тот процент, под который инвестор может получить средства для вложений (взять банковский кредит, продать свои акции или использовать внутренние средства).
• WACC – средневзвешенная стоимость капитала (от Weighted Average Cost of Capital) – если применяется сразу несколько источников привлечения денег, то процентная ставка будет представлять среднюю величину, рассчитанную пропорционально.

ВАЖНАЯ ИНФОРМАЦИЯ! Было бы очень просто рассчитать внутреннюю норму доходности, зная все необходимые показатели. Однако на практике невозможно определить точные величины денежных потоков и однозначно вычислить ставку дисконтирования. Поэтому для каждого отдельного проекта оценивают степень зависимости NPV от процентной ставки.

Формула расчета внутренней нормы рентабельности

IRR – это такая величина R, при которой NPV равен нулю. Поэтому этот показатель можно вывести из формулы расчета приведенной суммы денежных потоков.

• 0 означает величину NPV;
• n – количество исследуемых временных периодов;
• CF_t – денежные потоки в учетный момент времени.

Способы вычисления ВНД

Посчитать значение внутренней нормы доходности вручную не представляется возможным, так как, если вывести из него значение IRR, оно получится множителем 4 степени. Вычислить этот показатель можно несколькими способами:

• использовать специальный финансовый калькулятор;
• применить программу Excel, в которой эта функция встроена в раздел «Финансовые формулы» под названием ВСД («внутренняя ставка доходности»);
• воспользоваться одним из онлайн-калькуляторов;
• применить графический способ (использовался до широкого распространения Персональных компьютеров).

Достоинства и недостатки метода IRR

Для оценки инвестиционных возможностей главным образом применяются два метода – вычисление NPV и IRR. Метод определения внутренней нормы доходности относителен, поэтому не может претендовать на высокую точность, однако обладает рядом преимуществ:

• помогает достаточно просто оценить рентабельность инвестиционного проекта;
• показывает максимально допустимый размер затрат для вложения в проект;
• позволяет сравнивать различные проекты по рентабельности, даже если они отличаются по масштабу и протяженности во времени.

Недостатки метода IRR:

• нельзя посчитать абсолютную доходность инвестиции (то есть сколько конкретно денег – рублей, валюты – она может принести инвестору);
• возможно завышение инвестиционного эффекта, если ВНД сильно отличается от уровня реинвестиций компании (то есть положительные денежные потоки «возвращаются» инвестору с процентной ставкой, не совпадающей с ВНД);
• при вычислении имеет место пренебрежение последовательностью денежных потоков (для формулы не важно, в какой последовательности наступают затраты и приходит прибыль, тогда как на практике это может иметь решающее значение);
• возможны искажения при оценке взаимоисключающих инвестиционных проектов.

Интерпретация внутренней нормы доходности

Главное правило, по которому оценивают возможность инвестирования по показателю ВНД: проект можно принять, если IRR выше, чем средневзвешенная стоимость капитала для компании (WACC). Это значит, что инвестору стоит занимать деньги для вложения, и они, вероятнее всего, принесут добавочную прибыль.

НАПРИМЕР. Банк может предоставить инвестору деньги под 12% годовых. Инвестор собирается взять кредит и вложить средства в проект, ВНД которого 16%. Это значит, что 16% годовых – верхняя планка, по которой можно занять деньги для этого проекта. Если проект действительно принесет 16% прибыли, в пользу инвестора останется 4%, в любом случае он сможет вернуть заемные средства без убытка для себя.

Пример применения ВНД

Приведем жизненный пример оценки внутренней доходности, который может осознать обычный гражданин, а не только предприниматель.

Сдача квартиры в аренду – вроде бы выгодное мероприятие. Но все зависит от того, есть ли эта квартира в собственности. Если это так, то первоначальная инвестиция равна нулю, поэтому проект заведомо рентабелен. Но если планируется вложить средства в покупку квартиры, сдавать ее, а затем продать, чтобы вернуть взятый на это кредит?

Посчитаем, получится ли этот проект выгодным. Пусть квартира стоит 5 млн руб., а сумма аренды за год составит 25 000 руб. в месяц. Пренебрежем налоговыми расходами на оформление покупки квартиры и аренды. За 3 года доход от аренды составит 25 000 х 3 = 75 000 руб. Представим, что конъюнктура рынка недвижимости за 3 года не изменилась и квартиру удастся продать за цену покупки. Значит, спустя три года инвестиция принесет доход 75 000 + 5 млн руб. ВНД такого проекта получится равным приблизительно 6%.

Как известно, ставка кредитования в банке приблизительно составляет 9%, значит, имея в своем распоряжении свободные средства (например, получив их в наследство), их выгоднее положить на депозит, чем покупать квартиру с целью аренды.

Но если стоимость квартиры за эти годы существенно увеличится, ВНД проекта также изменится в лучшую сторону.

Источник

8.5. ВНУТРЕННЯЯ НОРМА ОКУПАЕМОСТИ ИНВЕСТИЦИЙ. ЧИСТАЯ ДИСКОНТИРОВАННАЯ СТОИМОСТЬ

Определение целесообразности осуществления инвестиций путем сопоставления предельной нормы окупаемости со ставкой процента возможно только по краткосрочным инвестициям. При оценке целесообразности долгосрочных инвестиций определяется внутренняя норма окупаемости инвестиций, или внутренняя норма доходности (Internal Rate of Return, IRR).

Чтобы определить внутреннюю норму окупаемости инвестиций, надо, ориентируясь на рассмотренный принцип дисконтирования, стоимость инвестиций в данный производственный объект приравнять к сумме доходов, которые этот объект даст за все годы его предполагаемого функционирования, причем процент r принять за неизвестное:

Решение такого уравнения относительно € позволит определить внутреннюю норму окупаемости данного инвестиционного проекта, т.к., € фактически характеризует темп, с которым сумма инвестиций, представляющая издержки по инвестированию, должна расти, чтобы обеспечивать доходы Rj.

Если эта норма будет больше ставки рыночного процента (т.е. если € > i), то фирме имеет смысл осуществлять данный инвестиционный проект, в противном случае инвестирование не имеет экономического смысла.

Рассмотрим на конкретном примере целесообразность осуществления инвестирования, опираясь на расчет внутренней нормы окупаемости инвестиций. Предположим, что решается вопрос о приобретении оборудования за 10 тыс. дол. Известно, что в течение первого года эксплуатации это оборудование не даст никакой прибыли, а в конце второго года обеспечит чистый доход в 12 тыс. дол. Внутренняя норма окупаемости будет рассчитываться следующим образом:

10 = 0 + 12 / (1 + € )2 , . € = 9,5%.

Если рыночная ставка равна, например, 10% годовых, то приобретение данного оборудования не представляется целесообразным, т.к.

Чистая дисконтированная стоимость. Решая вопрос о целесообразности новых инвестиций, фирма может также использовать показатель чистой дисконтированной (приведенной, текущей) стоимости (Net Present Value, NPV). Чтобы определить NPV инвестиционного проекта, надо сравнить объем инвестиций в данный проект с общей дисконтированной стоимостью будущих доходов, которые предполагается получить за период предстоящей эксплуатации этого объекта. Если предполагается, что инвестиции I в данный объект принесут в следующие десять лет прибыль в размере П1, П2, П3, . П10, то NPV будет равна:

NPV = –I + П1 / (1 +R) + П2 /(1 +R)2 +П3 /(1 +R)3 + . +П10 / (1 +R)10 .

Как видим, NPV представляет собой суммарную приведенную стоимость доходов за вычетом затрат, т.е. фактически характеризует чистую прибыль фирмы от инвестиций. Фирме следует осуществлять инвестиции только тогда, когда чистая прибыль положительна, т.е. когда NPV > 0.

При расчете NPV очень важно правильно сориентироваться относительно R, т.к. R в данном случае — это та норма прибыли, которую фирма могла бы получить от аналогичных инвестиций. Под аналогичными понимаются инвестиции с таким же риском. Поскольку чем более рискованным является тот или иной вариант инвестирования, тем больше ожидаемая от него прибыль, следовательно, высокорискованные инвестиционные проекты при расчете NPV должны исходить из достаточно высоких значений R. Напротив, если данный проект совсем не связан с риском (т.е. фирма уверена, что будущие доходы составят П1, П2 и т.д.), то вмененные издержки на инвестирование такого проекта следует считать равными прибыли, совсем свободной от риска. В качестве нормы прибыли, на которую следует ориентироваться в случае выбора безрискового проекта, можно использовать норму прибыли, получаемую от государственных облигаций. Если, например, данный инвестиционный проект рассчитан на десять лет, то фирма для вычисления по этому проекту NPV может использовать годовую ставку процента по десятилетней государственной облигации.

Предположим, имеется инвестиционный проект, рассчитанный на девять месяцев, который предполагает затраты в размере 1000 ден. ед., доход в 300 ден. ед. через три месяца и доход в 1000 ден. ед. через девять месяцев. В качестве альтернативного инвестиционного решения по данному проекту рассматривается банковский депозит, обеспечивающий доходность в 40% годовых с ежеквартальной выплатой процентов (10% суммы вклада выплачиваются каждые три месяца). NPV данного проекта будет равна:

NPV = –1000 + 300 / (1 + 0,4/4)1 + 1000 / (1 + 0,4/4)3 = 24,04 ден. ед.[25]

Поскольку NPV > 0, то данный проект выгоден.

Если данный инвестиционный проект предполагает осуществление инвестиций в течение ряда лет, то NPV такого инвестиционного проекта будет определяться путем сопоставления суммарной дисконтированной стоимости доходов, обеспечиваемых данным проектом, и суммарной дисконтированной стоимости затрат, т.е. NPV в этом случае будет оцениваться путем сравнения сегодняшней стоимости, будущих доходов и будущих затрат.

Из характеристики содержания чистой дисконтированной стоимости очевидно, что существует объективная связь между величиной NPV и процентной ставкой. Как правило, наблюдается обратная зависимость между данными величинами. Так получается потому, что высокая процентная ставка обычно снижает сегодняшнюю стоимость будущих доходов более значительно, чем стоимость будущих затрат, которые чаще всего производятся в большем объеме в начальные периоды реализации инвестиционного проекта. Графически типичный вариант взаимосвязи чистой дисконтированной стоимости и ставки процента может быть представлен следующим образом (рис. 8.6)[26]:

Как видно из графика, чем больше ставка процента, тем меньше значение NPV. При относительно невысоких ставках процента (до точки пересечения кривой NPV с линией ставки процента) чистая дисконтированная стоимость хотя и снижается, но остается положительной. При высоких ставках процента NPV принимает отрицательные значения, т.е. реализация проекта утрачивает экономический смысл. Точка пересечения кривой NPV и линии i характеризует такое значение ставки процента, при котором сегодняшняя стоимость затрат равняется сегодняшней стоимости доходов, т.к. в этой точке NPV = 0. Соответственно, значение процентной ставки i в данной точке является внутренней нормой окупаемости данного проекта.

Как показывают характеристики рассмотренных нами двух важнейших критериев эффективности инвестиционных решений — внутренней нормы окупаемости инвестиций и чистой дисконтированной стоимости, каждый из них способен обеспечивать достаточно надежные оценки целесообразности или нецелесообразности осуществления тех или иных инвестиций. Вместе с тем при оценках различных вариантов инвестиционных проектов считается полезным использовать оба данных критерия.

Предположим, например, что имеются два инвестиционных проекта, зависимости NPV которых от процентной ставки на графике представлены следующим образом (рис. 8.7)[27]:

Рис. 8.7. Сравнение критериев NPV и IRR

Как видно из рисунка, точка пересечения кривой NPV с линией i более отдалена от начала координат у второго проекта. Следовательно, второй проект имеет более высокую внутреннюю норму доходности, чем первый. Вместе с тем при процентной ставке i1 более выгодным оказывается первый проект, т.к. его чистая дисконтированная стоимость выше, чем у второго проекта.

Степень доверия инвесторов к финансовому рынку и успешность их участия в работе данного рынка существенно зависят от информационной эффективности финансового рынка.

Как уже отмечалось, при оценке чистой дисконтированной стоимости инвестиционных проектов важно правильно выбрать норму прибыли, на которую инвестор мог бы ориентироваться. Данная норма прибыли, или ставка дисконтирования, должна характеризовать доходность альтернативных инвестиций с такой же или сравнимой степенью риска. Такой подход к определению ставки дисконтирования важен потому, что данная ставка должна соответствовать степени уверенности инвестора в получении будущего дохода. Если инвестор не склонен к риску, то два альтернативных инвестиционных проекта — безрисковый и рискованный — будут для него эквивалентны только в том случае, если ожидаемая доходность рискованного проекта будет превышать безрисковую доходность, т.е. включать в себя премию за риск.

Принимая решение о вложениях своих средств, инвестор учитывает не только свои цели и предпочтения относительно риска и дохода, но и по возможности истинные стоимости тех или иных финансовых активов. Степень точности оценок инвесторами истинной стоимости активов зависит от полноты и точности их информации о тех факторах, которые влияют или могут повлиять на будущие доходы в связи с использованием данных активов. Поскольку цены финансовых активов формируются под воздействием спроса и предложения, то от полноты и точности таких оценок истинной стоимости активов зависит степень информационной эффективности данного рынка. Если, например, значительная (преобладающая) часть участников рынка будет оценивать тот или иной актив выше его текущей рыночной цены, т.е. будет считать данный актив недооцененным, то спрос на этот актив начнет повышаться, что приведет к росту его цены. Напротив, если бы бoльшая часть инвесторов посчитали, что актив переоценен рынком, то его предложение возросло бы и цена стала бы снижаться. Таким образом, цены финансовых активов на нормально работающих рынках всегда примерно соответствуют оценкам их истинной стоимости со стороны большинства инвесторов, и важно лишь, точны ли эти оценки.

Согласно гипотезе об информационной эффективности финансового рынка участники рынка верно оценивают истинные стоимости финансовых активов, в результате чего рыночные цены активов соответствуют их истинной стоимости.

Строгая форма эффективности финансового рынка означает предположение, что цены на этом рынке в точности соответствуют инвестиционной стоимости активов и что, следовательно, активы оценены с использованием абсолютно полной и точной информации и самых совершенных методов оценки. Такая форма эффективности финансового рынка отражает представления об идеальном варианте работы данного вида рынка, т.к. в реальной практике всегда имеются факты либо запаздывания, либо недоступности хотя бы части информации, либо вообще отсутствия таковой.

Более реалистичным является предположение о полустрогой форме эффективности финансового рынка, согласно которому цены финансовых активов отражают не абсолютно всю, а лишь общедоступную для инвесторов информацию об этих активах.

Если исходить из предположения о слабой форме информационной эффективности финансового рынка, то это будет означать, что оценки инвесторами истинной стоимости финансовых активов предполагаются на основе исторической (прошлой) информации.

Чем выше степень информационной эффективности финансового рынка, тем меньше возможностей для осуществления на этом рынке спекулятивных арбитражных операций. Арбитраж означает получение гарантированной положительной прибыли при нулевых инвестициях вследствие более высокой точности оценок истинной стоимости финансовых активов спекулянтами–арбитражерами по сравнению с рыночными ценами. Если же в текущей рыночной цене будет учтена вся информация, имеющая значение для данного актива, то более точные оценки его стоимости, чем оценка самого рынка, будут просто невозможными. В результате информационно эффективный рынок обеспечивает наиболее точное прогнозирование доходности и степени риска инвестиций. Если же рынок характеризуется слабой формой информационной эффективности, то прогнозировать будущие изменения цены на основе прошлой информации и получать на основе этих прогнозов арбитражную прибыль оказывается невозможным. Если рынок эффективен в слабой форме, то справедливой является гипотеза случайного шага: цена отражает всю прошлую информацию о данном активе, следовательно, колебания цен на рынке представляют собой случайный процесс.

От того, насколько высока или низка информационная эффективность финансового рынка, во многом зависит общеэкономическая эффективность распределения ресурсов в экономике. По В. Парето, как известно, экономически эффективным распределением ресурсов является такое распределение, при котором выгоды от использования ресурсов равны альтернативной стоимости этих ресурсов. Из приведенного ранее материала следует, что применительно к финансовому рынку это общее правило выражается равенством рыночной цены и инвестиционной стоимости финансовых активов: P = V, где V представляет собой суммарную дисконтированную стоимость будущих доходов от того или иного финансового актива (объекта инвестирования). Если данное равенство не будет выполняться, то это будет означать, что инвестиционные ресурсы (сбережения) распределяются неэффективно. Если цены окажутся выше дисконтированной стоимости будущих доходов (P> V), то это будет означать, что относительно выгодные проекты финансируются в недостаточных объемах. Если же сформируется неравенство обратного порядка (P

Источник