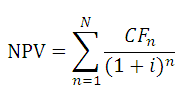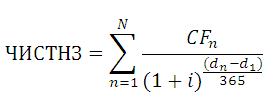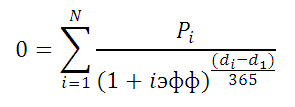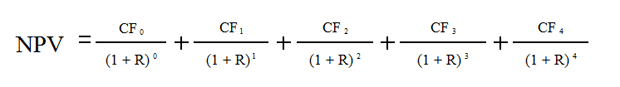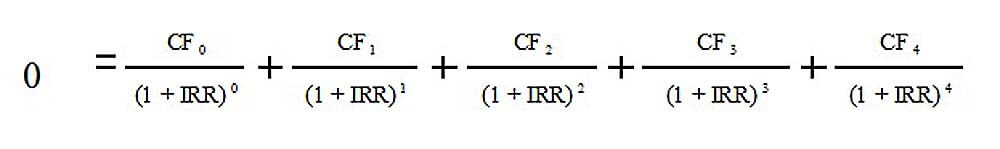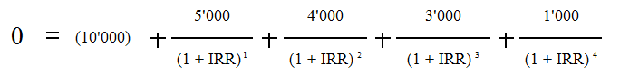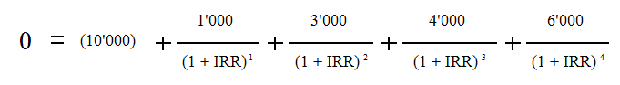Внутренняя норма доходности формула эксель

Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL

history 3 февраля 2015 г.

Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.

Начнем с определения, точнее с определений.

Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : « ИНФРА — М «, Издательство « ВесьМир «. Дж . Блэк .)

Примечание1 . Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется ЧПС() , то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с Приведенной стоимостью .

Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.

Совет : при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи Приведенная стоимость .

Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу сложных процентов .

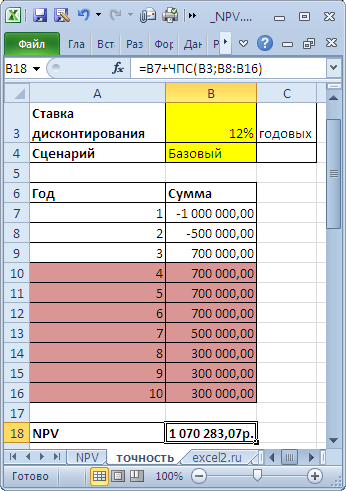
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция ЧПС() (английский вариант — NPV()). В ее основе используется формула:

CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).

Примечание2 . Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить: Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год) . Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).

Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV Примечание3 . Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.

Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).

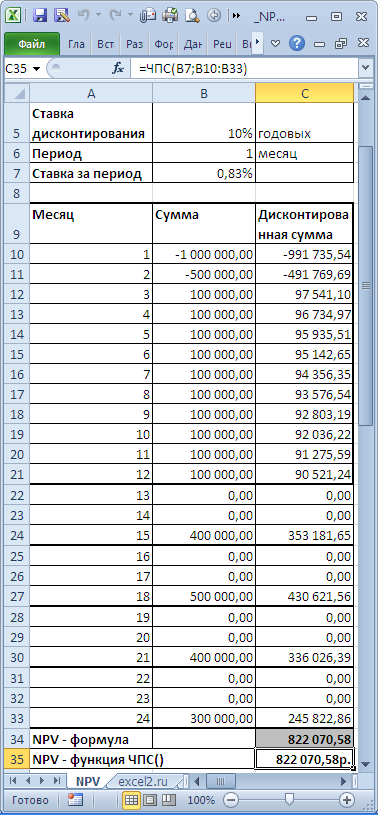
В таблице NPV подсчитан двумя способами: через функцию ЧПС() и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции ЧПС() , а нужно просто прибавить к получившемуся результату (см. файл примера ). Сравнение 2-х вариантов дисконтирования приведено в файле примера , лист NPV:

О точности расчета ставки дисконтирования

Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).

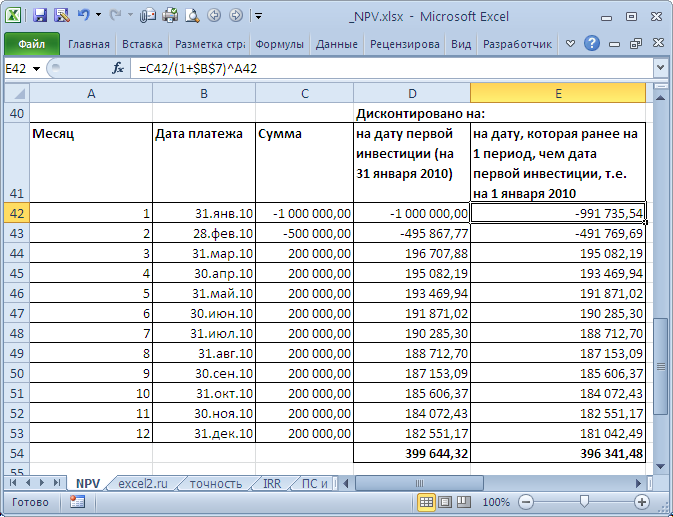
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.

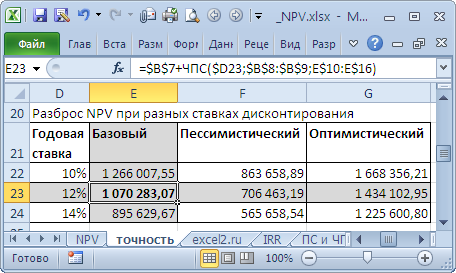
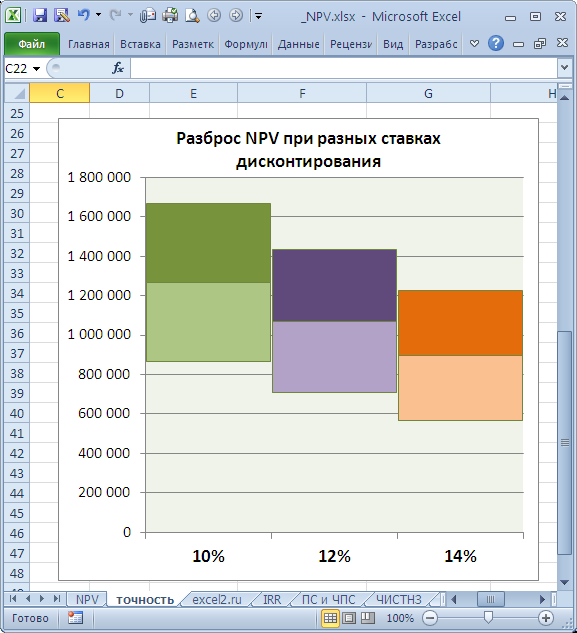
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):

Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.

Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.

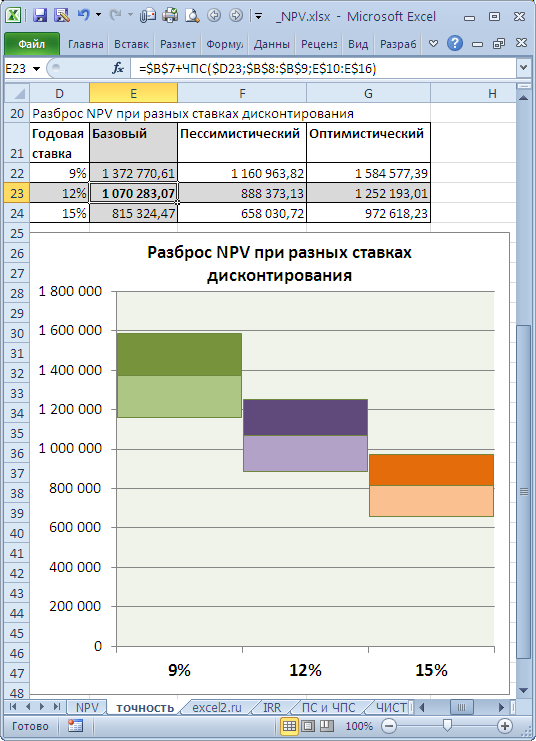
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0

Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.

Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.

После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.

Внутренняя ставка доходности IRR (ВСД)

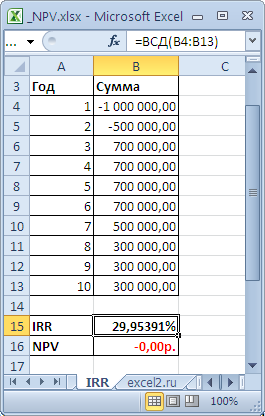
Внутренняя ставка доходности (англ. internal rate of return , IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см. файл примера, лист IRR ).

Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

Для расчета IRR используется функция ВСД() (английский вариант – IRR()). Эта функция тесно связана с функцией ЧПС() . Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией ВСД() , всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле: =ЧПС(ВСД(B5:B14);B5:B14)

Примечание4 . IRR можно рассчитать и без функции ВСД() : достаточно иметь функцию ЧПС() . Для этого нужно использовать инструмент Подбор параметра (поле «Установить в ячейке» должно ссылаться на формулу с ЧПС() , в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).

Расчет NPV при постоянных денежных потоках с помощью функции ПС()

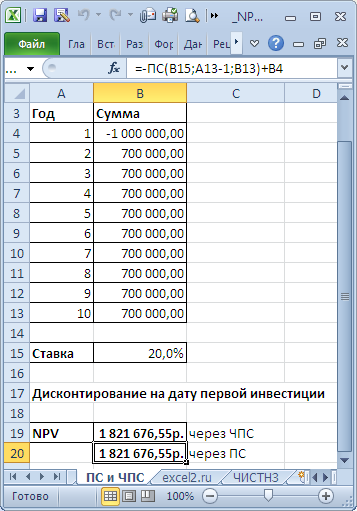
Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).

В этом случае все денежные потоки (диапазон В5:В13 , 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке В4 . Ставка дисконтирования расположена в ячейке В15 со знаком минус. В этом случае формула =B4+ЧПС(B15;B5:B13) дает тот же результат, что и = B4-ПС(B15;9;B13)

Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени

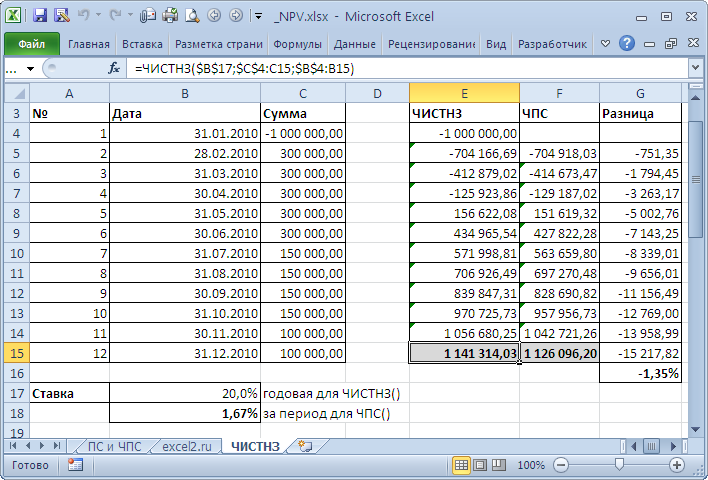
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).

Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:

Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.

Принципиальным отличием от ЧПС() является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у ЧИСТНЗ() всегда годовая, т.к. указана база 365 дней, а не за период, как у ЧПС() . Еще отличие от ЧПС() : все денежные потоки всегда дисконтируются на дату первого платежа.

В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций ЧИСТНЗ() и ЧПС() . Эти функции возвращают несколько отличающиеся результаты. Для задачи из файла примера, Лист ЧИСТНЗ разница составила порядка 1% (период = 1 месяцу).

Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).

Внутренняя ставка доходности ЧИСТВНДОХ()

По аналогии с ЧПС() , у которой имеется родственная ей функция ВСД() , у ЧИСТНЗ() есть функция ЧИСТВНДОХ() , которая вычисляет годовую ставку дисконтирования, при которой ЧИСТНЗ() возвращает 0.

Расчеты в функции ЧИСТВНДОХ() производятся по формуле:

Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).

Источник

МСФО, Дипифр

Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта.

IRR — это Internal Rate of Return, что переводится на русский язык как «внутренняя норма доходности». Так называется один из двух основных методов оценки инвестиционных проектов. В интернете немало статей, представляющих собой краткое изложение данной темы по учебникам финансового анализа. Их общий минус в том, что в них слишком много математики и слишком мало объяснений.

В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя и интерпретации полученных результатов.

IRR — что это такое? Формула IRR.

IRR или внутренняя норма доходности — это ставка процента, при которой приведенная стоимость всех денежных потоков инвестиционного проекта (т.е. NPV) равна нулю. Это означает, что при такой ставке процента инвестор сможет возместить свою первоначальную инвестицию, но не более того. О том, как пользоваться показателем IRR для одобрения инвестиционных проектов рассказывается чуть дальше в этой статье. Для начала надо научиться рассчитывать величину внутренней нормы доходности IRR, или, как ее еще называют, внутренней нормы рентабельности.

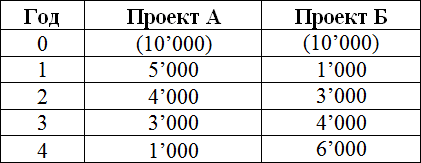
Математика расчета IRR довольно простая. Лучше всего рассмотреть ее на элементарных примерах. Для расчета показателя NPV инвестиционного проекта в одной из более ранних статей на этом сайте были использованы проекты А и Б с одинаковой суммой первоначальной инвестиции (10,000), но с разными по величине притоками денежных средств в последующие 4 года. Удобно будет воспользоваться этими примерами и для изучения формулы расчета показателя IRR.

Приведенная (к сегодняшнему моменту) стоимость всех денежных потоков для четырехлетних проектов будет вычисляться по формуле:

где NPV — чистая приведенная стоимость, CF — денежные потоки (Cash Flows), R — % ставка, стоимость капитала, 0,1,2,3,4 — количество периодов времени от сегодняшнего момента.

Если приравнять NPV к нулю, а вместо CF подставить денежные потоки, соответствующие каждому проекту, то в уравнении останется одна переменная R. Ставка процента, которая будет решением данного уравнения, т.е. при которой сумма всех слагаемых будет равна нулю, и будет называться IRR или внутренней нормой доходности.

Для проекта А уравнение примет вид:

Для проекта Б можно написать аналогичную формулу для расчета IRR, только денежные потоки будут другими:

Чтобы было еще понятнее, можно нанести денежные потоки от проекта на шкалу времени и представить дисконтирование наглядно. Скажем, для проекта А расчет внутренней нормы доходности можно представить в таком виде:

В общем виде для любого инвестиционного проекта формула для расчета IRR выглядит так:

где CF _t — денежные потоки от проекта в момент времени t , n — количество периодов времени, IRR — внутренняя норма доходности. Обратите внимание, что понятие IRR в отличие от NPV имеет смысл только для инвестиционного проекта, т.е. когда один из денежных потоков (обычно самый первый) является отрицательным. Этот отрицательный денежный поток и будет являться первоначальной инвестицией. В противном случае мы никогда не получим NPV, равную нулю.

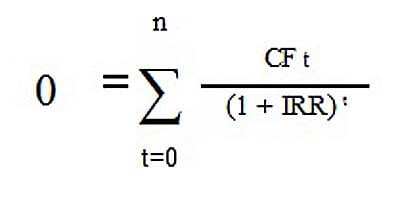
Расчет внутренней нормы доходности с помощью программы Excel — примеры

Вручную с помощью обычного калькулятора найти значение IRR для проектов А и Б невозможно, потому что в данном случае получается уравнение 4-й степени (в нем будет множитель IRR 4 — ставка процента в четвертой степени). Проблему решения такого уравнения n-ой степени можно устранить или с помощью финансового калькулятора, или, что проще, можно воспользоваться встроенной функцией в программе Excel. Эта функция находится в разделе Формулы —> Финансовые, и называется она ВСД (внутренняя ставка доходности).

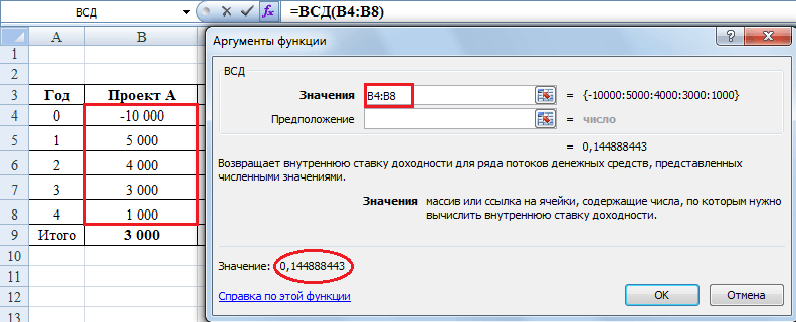
Для проекта А значение IRR, как видно из рисунка ниже, составит 14,48%.

Чтобы воспользоваться функцией ВСД, в строку «значения» нужно поставить ссылки на ячейки таблицы с суммами денежных потоков. Ячейку «предположение» можно не заполнять, этот аргумент, является необязательным. Выводимое значение 0,144888443 — это и будет искомая IRR, т.е. внутренняя норма доходности данного проекта. Если перевести эту величину в проценты, то она равна 14,48% с точностью до двух знаков после запятой.

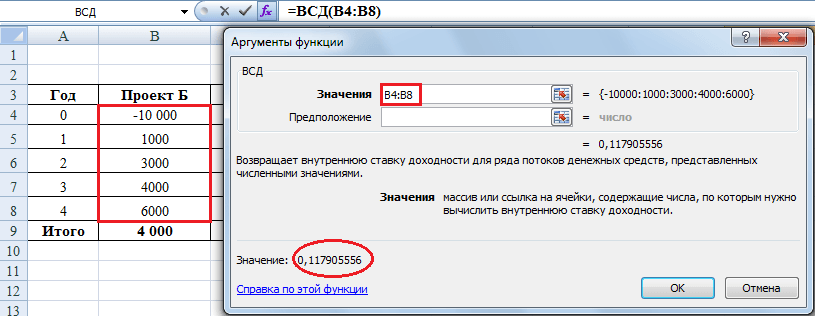
Для проекта Б значение IRR согласно Excel равно 11,79%.

Приведу важные пояснения по этой функции из раздела «справка» с моими дополнениями:

1. Значения должны содержать по крайней мере одну положительную и одну отрицательную величину. В противном случае функция ВСД возвращает значение ошибки #ЧИСЛО!. Действительно, если нет отрицательного денежного потока, то NPV не может быть равно нулю, а в этом случае IRR не существует.
2. Для расчета функции ВСД важен порядок поступлений денежных средств. Поэтому если потоки денежных средств отличаются по величине в разные периоды, что обычно и бывает, то их необходимо внести в таблицу в соответствии со временем их возникновения.
3. В Microsoft Excel для вычисления ВСД используется метод итераций. Функцией ВСД выполняются циклические вычисления начиная со значения аргумента «предположение», пока не будет получен результат с точностью 0,00001%. В большинстве случаев для вычислений с помощью функции ВСД нет необходимости задавать аргумент «предположение». Если он опущен, предполагается значение 0,1 (10%).

Другими словами функция ВСД программы Excel будет искать значение IRR подбором, последовательно подставляя в формулу различные величины % ставки, начиная со значения в ячейке «предположение» или с 10%. Если функция ВСД не сможет получить результат после 20 попыток, выдается значение ошибки #ЧИСЛО! Поэтому в некоторых случаях, например, если вы будете считать IRR для ежемесячных потоков за несколько лет, лучше поставить в ячейку «предположение» ожидаемую вами величину ежемесячной процентной ставки. Иначе Excel может не справиться с расчетом за 20 попыток.

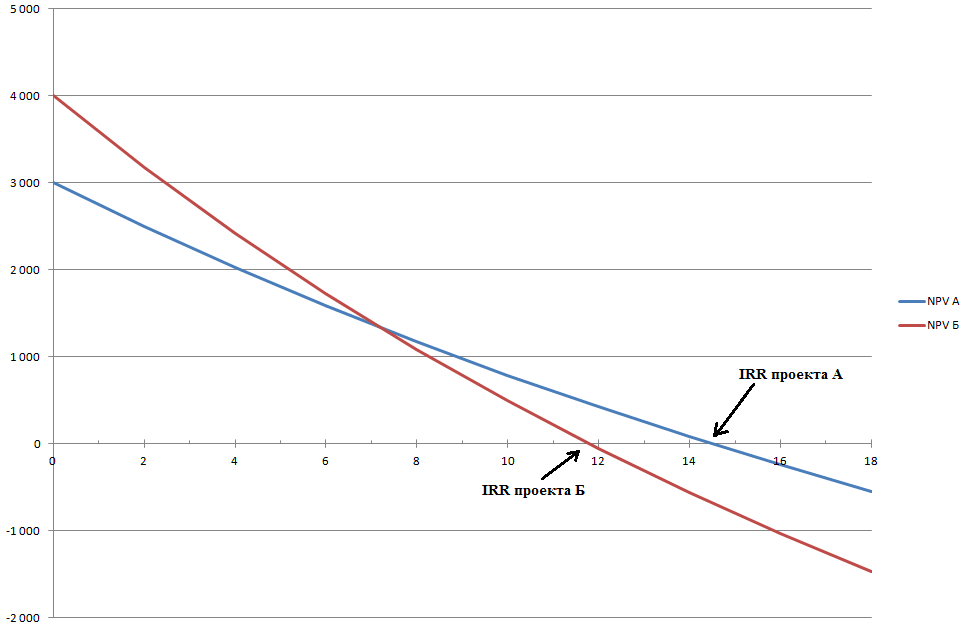
Графический метод расчета IRR

До появления персональных компьютеров обычно использовался графический метод определения IRR. Ниже представлены графики изменения NPV для проектов А и Б в зависимости от ставки процента. Для построения графиков нужно найти значение NPV, подставляя в формулу NPV различные значения ставки дисконтирования. Что такое дисконтирование и как дисконтировать денежные потоки, можно прочитать в одной из моих предыдущих статей.

На рисунке выше синий график — проект А, красный график — проект Б. Пересечение графиков с осью X (в этой точке NPV проекта равно нулю) как раз и даст значение IRR для этих проектов. Нетрудно видеть, что графический метод дает величину IRR, аналогичную найденным в Excel значениям внутренней нормы доходности для проектов А — 14,5% и Б — 11,8%.

Как пользоваться показателем IRR для оценки инвестиционных проектов?

Любой инвестиционный проект предполагает наличие первоначальной инвестиции (оттока денежных средств), которая приведет к поступлениям денежных средств в будущем (в идеальном случае). Что же показывает внутренняя норма доходности инвестиционного проекта? Она показывает ставку кредита, при которой мы не получим убытка от нашей инвестиции, т.е. результатом всех денежных притоков и оттоков в сумме будет ноль — ни прибыли, ни убытка. В этом случае наша инвестиция в проект окупится будущими поступлениями денежных средств от проекта, но в конечном итоге мы ничего не заработаем.

Правило оценки инвестиционных проектов:

Если величина IRR проекта больше стоимости капитала для компании (т.е. WACC), то проект следует принять.

Другими словами, если ставка кредита меньше ставки инвестирования (внутренней нормы доходности проекта), то заемные деньги принесут добавочную стоимость. Потому что такой инвестиционный проект заработает больший процент дохода, чем стоимость капитала, которая необходима для первоначальной инвестиции.

Например, если вы берете кредит в банке под 14% годовых для того, чтобы вложить средства в бизнес-проект, который принесет вам 20% годовых дохода, то вы на этом проекте заработаете. Если же ваши расчеты окажутся неверны, и внутренняя норма доходности вашего проекта будет ниже 14%, то вам придется отдать банку больше денежных средств, чем вы получите от проекта. То есть вы понесете убыток.

Сам банк поступает точно так же. Он привлекает деньги от населения, скажем, под 10% годовых (ставка по депозиту), а выдает кредиты под 20% годовых (цифра взята «с потолка»). До тех пор, пока ставка по принимаемым банком депозитам будет меньше, чем ставка по выдаваемым банком кредитам, банк будет жить на эту разницу.

Рассчитав показатель IRR, мы узнаем верхний допустимый уровень стоимости заемного капитала, который предполагается инвестировать. Если стоимость капитала (по которой компания может привлечь финансовые ресурсы) выше, чем внутренняя доходность проекта (IRR), то проект принесет убытки. Если стоимость капитала для компании ниже, чем IRR проекта, то компания в каком-то смысле будет работать как банк — жить на разницу между процентными ставками банковского кредитования и рентабельности инвестиции.

Чтобы логика расчета IRR стала еще понятнее, приведу несколько примеров из жизни, с которыми может столкнуться (и сталкивается) обычный человек.

Пример 1 — срочный вклад в Сбербанке

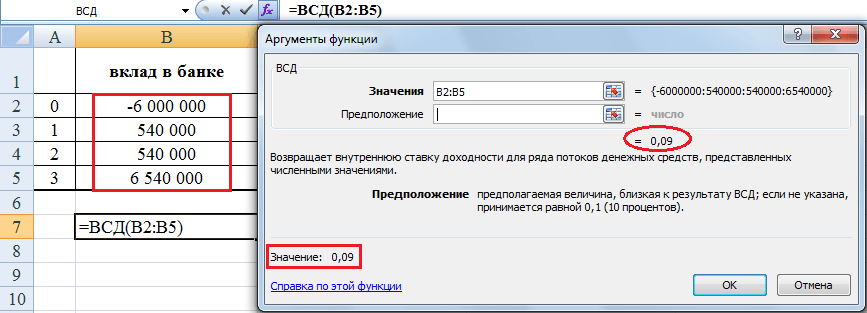
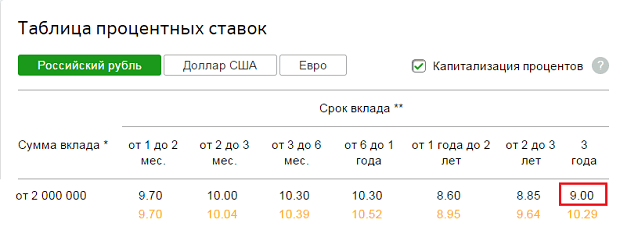
Допустим, у вас есть в наличии 6,000,000 рублей. Прямо сейчас можно сделать срочный вклад в Сбербанк, скажем, на три года. Сумма большая, поэтому нужен самый надежный банк в России. Сбербанк в данный момент предлагает ставку для вкладов свыше 2 млн. рублей на три года в размере 9,0 % годовых без капитализации и 10,29% годовых с ежемесячной капитализацией. Что такое капитализация вклада можно прочитать по ссылке.

Поскольку мы будем снимать проценты в конце каждого года, это будет вклад без капитализации процентов, и ставка составит 9% годовых. В конце каждого года можно будет снимать сумму, равную 6,000,000*0,09 = 540,000 рублей. В конце третьего года депозит можно будет закрыть, сняв проценты за третий год и основную сумму в размере 6 миллионов рублей.

Вклад в банке — это тоже инвестиционный проект, поскольку сначала делается первоначальная инвестиция (отрицательный денежный поток), а потом собираются денежные притоки от нашего проекта. Банковский депозит — это финансовый инструмент, и самый простой способ инвестирования, доступный для обычного человека. Раз это инвестиционный проект, то можно рассчитать его внутреннюю норму доходности. Наверное, многие уже догадались, чему она будет равна.

Внутренняя норма доходности (IRR инвестиции) в банковский депозит равна процентной ставке по этому депозиту, т.е. 9%. Если 6,000,000 рублей достались вам в наследство после уплаты налогов, то это означает, что стоимость капитала для вас равна нулю. Поэтому такой инвестиционный проект будет выгоден при любой депозитной ставке. Но взять кредит на 6 миллионов в одном банке и положить эти деньги на депозит в другой банк с прибылью не получится: ставка кредита всегда будет заведомо выше ставки инвестирования. Это принцип работы банковской системы.

Пример 2 — покупка квартиры с целью заработка на сдаче ее в аренду

Свободные денежные средства можно использовать и по-другому, а именно купить квартиру в Москве, сдавать ее в аренду три года, а в конце третьего года продать эту квартиру, чтобы вернуть основной капитал. Денежные потоки от такого проекта будут очень похожи на потоки денежных средств от срочного вклада в банке: примем, что арендная плата для простоты расчета уплачивается арендатором квартиры сразу за год в конце каждого года, а стоимость квартиры в рублях через три года останется такой же, как и сейчас. Я намеренно упрощаю ситуацию, более сложные расчеты вы сможете сделать самостоятельно.

Я выбрала в Интернете первую же попавшуюся квартиру за 6 млн. рублей на СЗ Москвы. Аренда подобной однокомнатной квартиры стоит 30,000 рублей в месяц. Налоговые последствия данных сделок для простоты не учитываются.

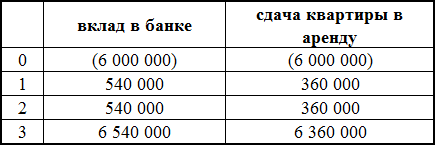
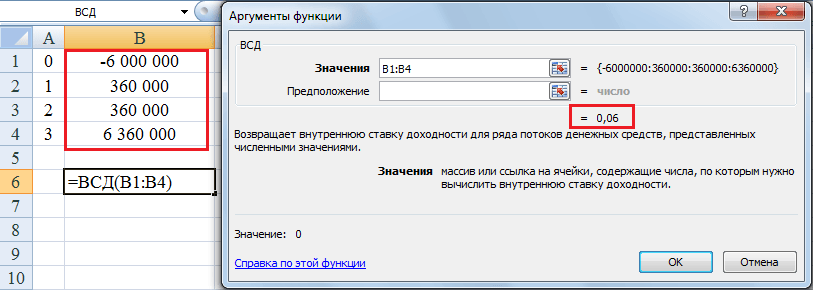
Итак, арендная плата за год составит 30,000*12 = 360,000 рублей. Чтобы было нагляднее, денежные потоки от обоих проектов — вклад в Сбербанке и сдача 1-комнатной квартиры в аренду на северо-западе Москвы — показаны вместе в таблице ниже:

Даже без вычисления IRR видно, что сейчас банковский депозит является более доходным вариантом. Легко доказать это, если рассчитать внутреннюю норму доходности для второго проекта — она будет ниже, чем IRR по депозиту. При сдаче данной однокомнатной московской квартиры в течение трех лет при условии ее продажи в конце третьего года IRR инвестиции составит 6,0% годовых.

Если у вас нет наследства в сумме 6 млн рублей, то брать эти деньги в кредит, чтобы сдавать квартиру в аренду неразумно, так как ставка кредитования сейчас заведомо выше, чем 6,0% внутренней доходности данного проекта. Причем IRR не зависит от количества лет сдачи квартиры в аренду — внутренняя норма доходности останется такой же, если вместо трех лет сдавать ее в аренду 10 лет или 15.

Если учесть ежегодное подорожание квартиры в результате инфляции, IRR данного проекта будет выше, Например, если в первый год (2015) рублевая стоимость квартиры вырастет на 10%, во второй (2016) на 9%, а в третий (2017) на 8%, то к концу третьего года ее можно будет продать за 6,000,000*1,10*1,09*1,08 = 7,769,520 рублей. Такое увеличение денежного потока в третий год проекта даст IRR, равную 14,53%. Поэтому если бы мы могли предсказать будущие рублевые цены на квартиры с большой точностью, то наш проект стал бы более реальным. Но все равно невыгодным в нынешней ситуации, когда ставка рефинансирования ЦБ равна 17%, и, соответственно, все банковские кредиты слишком дороги.

Расчет IRR при ежемесячных потоках денежных средств

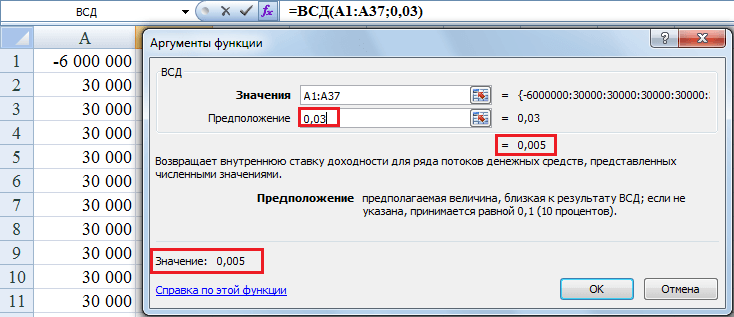
С помощью функции ВСД можно рассчитать IRR инвестиционного проекта при равных промежутках времени между денежными потоками. Результатом вычислений будет процентная ставка за период — год, квартал, месяц. Например, если бы мы считали, что платежи за аренду квартиры приходят в конце каждого месяца (а не года), то надо было бы сделать таблицу Excel с 36-ю платежами по 30,000 рублей. В этом случае функция ВСД выдала бы значение внутренней нормы доходности проекта за месяц. Для нашего проекта IRR получилась равной 0,5% в месяц. Это соответствует годовой % ставке в размере 6,17% (рассчитывается как (1+0,005) 12 -1), что ненамного больше, чем 6,0%, рассчитанных ранее.

Если вы захотите получить этот результат самостоятельно, обязательно заполните ячейку «предположение» — поставьте туда 0,03, иначе вы получите на выходе ошибку #ЧИСЛО!, потому что Excel не хватит 20 попыток, чтобы рассчитать IRR.

Расчет IRR при неравных промежутках времени между денежными потоками

Excel предоставляет возможность рассчитать внутреннюю норму доходности проекта и в том случае, если денежные потоки от проекта поступают через неравные промежутки времени. Для расчета IRR такого проекта надо использовать функцию ЧИСТВНДОХ и в качестве аргумента указать не только ячейки с денежными потоками, но и ячейки с датами их поступлений. Например, если мы перенесем срок продажи квартиры вместе с последней арендной платой на конец четвертого года (с 31.12.17 на 31.12.18), а в конце третьего года у нас не будет поступлений денежных средств, то IRR упадет с 6% до 4,53% годовых. Обратите внимание, что рассчитать внутреннюю норму доходности в данном случае можно будет только с помощью функции ЧИСТВНДОХ, потому что фукция ВСД даст тот же результат, который и был — 6%, т.е. изменение периода времени ВСД не учтет.

«Куда идем мы с Пятачком, большой, большой секрет…»

(Мнение автора может не совпадать с мнением правительства)

Нынешняя ставка рефинансирования, равная 17%, убивает и бизнес, и банки. Потому что трудно найти инвестиционные проекты, которые бы окупались при таких ставках кредитования. Как развивать бизнес в подобных условиях? Торговля оружием и наркотиками, конечно, будут прибыльны и в этом случае, но большая часть бизнесов будут в лучшем случае выживать, а в худшем разорятся.

И как будут зарабатывать банки, если инвестиционных проектов с такой высокой доходностью просто не существует? А чтобы платить нам выросшие проценты по вкладам, банки должны где-то зарабатывать средства для этого.

Россия смогла бы выдержать и более низкий курс рубля по отношению к основным валютам, но справиться еще и с высокой процентной ставкой в экономике — это уже перебор.

В 2014 году мы неоднократно слышали, что ЦБ РФ занимается таргетированием инфляции. И делалось это с благими намерениями — чем ниже инфляция, тем легче добиться окупаемости инвестиций. Но получается, что хотели «как лучше», а получилось «как всегда». При дорогой валюте, как сейчас, в России могло бы успешно развиваться собственное производство, импортозамещение стало бы реальностью. Но нет, мы не ищем легких путей, а что хуже всего, мы не учимся на своих ошибках. И живем, как в том анекдоте:

«В прошлом году посеяли 100 га пшеницы. Все поел хомяк…В этом году собираемся засеять 200 га пшеницы. Нехай хомяк подавится!»

Не вписались в рынок — небольшая заметка о том, к чему привели высокие ставки по кредитам в 2014-15 годах. Хотя, конечно, сложно судить, что было бы лучше: еще более низкий курс рубля, но не такие высокие процентные ставки по кредитам для компаний, или то, что у нас в итоге получилось.

март 2018 «Эксперты не исключают кризиса плохих долгов в ближайшие годы. Об этом, в частности, заявил директор Центра структурных исследований РАНХиГС, экс-замминистра экономического развития Алексей Ведев. По его словам, это может случиться в ближайшие полтора-два года «с большой вероятностью».

Сейчас у банков накоплен портфель кредитов в 11 трлн рублей, размещенных под запредельные 16% годовых, с 2 триллионами рублей процентных платежей ежегодно, отметил Ведев. Это очень тяжелая нагрузка на заемщиков, на экономику. При этом основная задолженность приходится на слабо обеспеченные слои населения. «Ситуация близка к катастрофичной!», — считает он.

Другие статьи на этом сайте из рубрики «Финансы»:

Источник