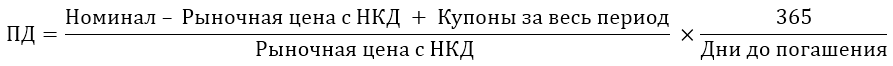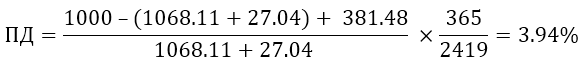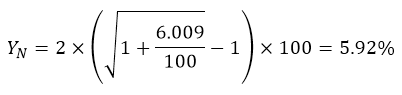- Доходность облигаций: виды и расчет
- Виды доходности облигаций
- дисконтная
- купонная
- текущая
- простая
- эффективная
- номинальная
- 1. Доходность дисконтной облигации
- 2. Купонная доходность
- 3. Текущая доходность
- 4. Простая доходность к погашению
- 5. Эффективная доходность к погашению
- Доходность к оферте
- 6. Номинальная доходность
- Доходность облигаций на сайте Мосбиржи
- Доходность фондов облигаций
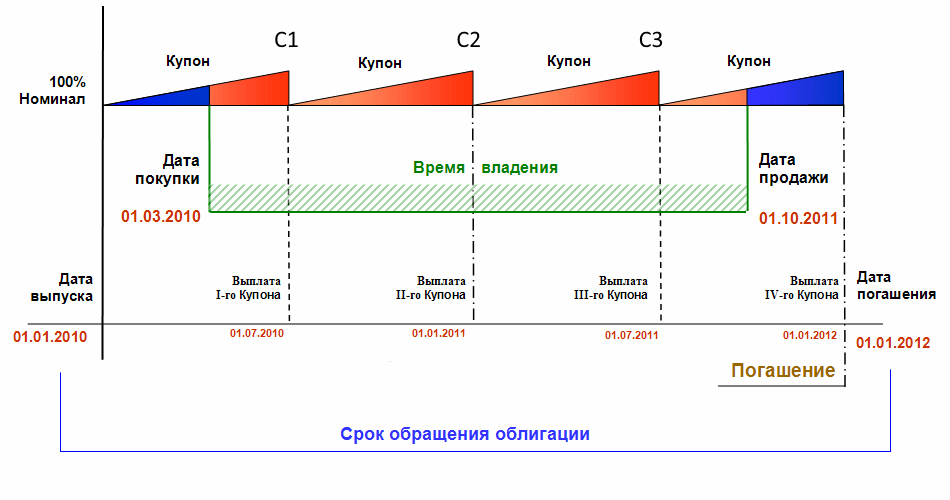
- Из чего состоит доход по облигации
- Виды доходности по облигациям
- Купонная
- Текущая
- Простая к погашению
- Эффективная к погашению
- Доходность к продаже
- Какие формулы используются при подсчете доходности бондов
- Как получить максимальный доход
Доходность облигаций: виды и расчет
Прежде чем обстоятельно поговорить о доходности облигаций, кратко вспомним основные определения. Облигация – это долговая ценная бумага, также называемая бонд (bond). Ее суть: инвестор дает эмитенту деньги в долг, а заем закрепляется распиской – облигацией. Инвестор это тот, кто купил облигацию. Эмитент выпускает ее в обращение.
Из каких элементов состоит доходность стандартных облигаций для инвестора:
- проценты – купоны
- продажа до погашения – разница между ценой покупки и реализации долговой бумаги
Купоны – это основной доход от бондов, ради которого, как правило, их и приобретают. Выплачиваются с определенной периодичностью – раз в год, полгода или квартал. Фонды из многих облигаций могут платить доход каждый месяц. Пример: облигация 1 000 руб. с купоном в 8% принесет инвестору доход за год: 1 000 р. × 8% = 80 руб.
Номинальная стоимость облигаций часто (но не всегда) остается неизменной на протяжении всего периода обращения. Самый распространенный номинал среди российских долговых бумаг равен 1 000 руб. А вот рыночная стоимость бондов меняется в силу различных факторов, причем главным внешним воздействием является ключевая ставка Центробанка.
Если вы купили долговую бумагу по цене ниже номинала, а продали по величине номинала, у вас возникает доход от продажи. Он называется дисконтом. Пример: номинальная стоимость бумаги равна 1 000 руб., но вы купили ее за 900, а затем продали по номиналу (додержали до погашения). Дисконт составил 100 руб или 10% прибыли.
Виды доходности облигаций
Есть разные показатели доходности, по которым инвестор сравнивает облигации и выбирает наиболее выгодные для себя варианты. Рассмотрим доходность бондов по следующей классификации:
дисконтная
купонная
текущая
простая
эффективная
номинальная
1. Доходность дисконтной облигации
Дисконтная облигация чаще всего выплачивает доход единоразово в момент погашения. Скажем, вы купили бумагу за 500 рублей и через несколько лет получаете 1000. Это облегчает расчет и понимание смысла дохода, поскольку нет промежуточных выплат в течение всего срока владения бумагой. Формула доходности:
Доходность = (Номинал/Текущая цена) (1/Количество лет до погашения) -1
Номинал в данном случае это сумма, которую получит покупатель облигации в конце обозначенного срока, если эмитент не объявит банкротство. Возьмем срок до погашения 10 лет, номинал 50 тысяч рублей и текущую цену в 20 тысяч. Подставляя эти данные в формулу, получим 9.6% годовых. Обычно такие бонды выгодны по доходности, если являются долгосрочными — поскольку обладают более высоким риском. О дисконтных облигациях читайте здесь.
2. Купонная доходность
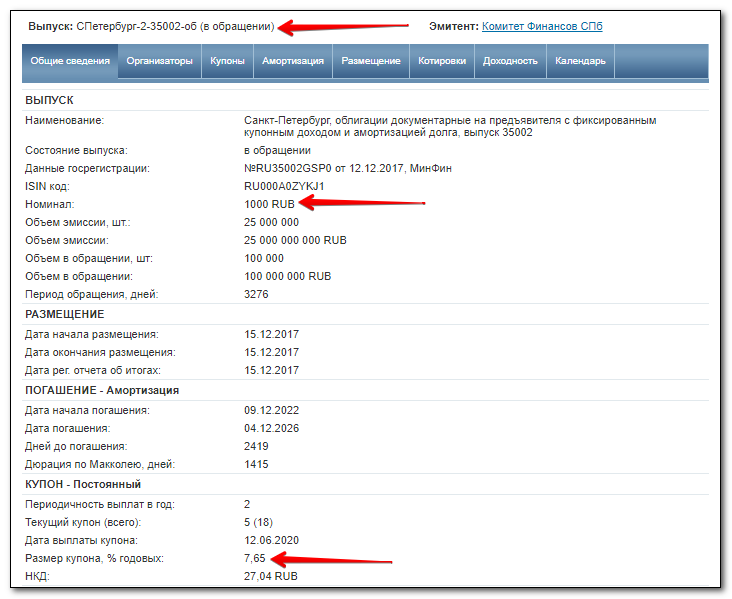
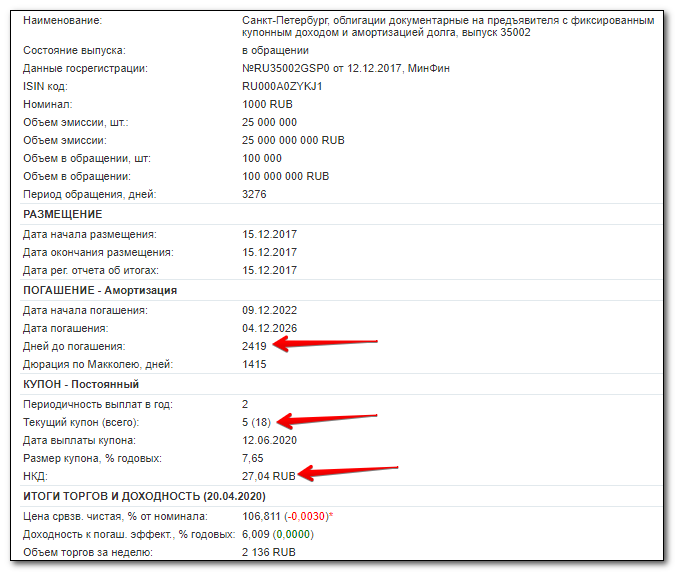
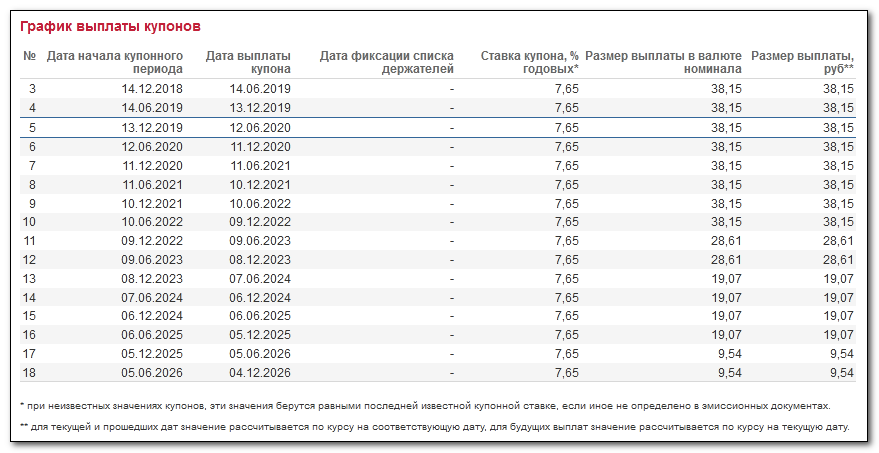
Наиболее легкий вариант измерения доходности облигаций – по размеру купона. Вот реальная облигация с сайта rusbonds.ru , обращающаяся на рынке:
Это муниципальная облигация, выпускаемая Комфином Санкт-Петербурга. При номинале 1 000 руб. и процентной ставке 7,65%, купонная доходность составляет 7,65% за год. Значит, годовой доход одной облигации на текущий момент равен 76,5 руб. Правда, поскольку данная бумага выпущена с амортизацией, с конца 2022 года реальные выплаты будут уменьшаться.
Если проценты выплачиваются не раз в год, а чаще, например, раз в полгода, то купон за такой укороченный период составит 7,65% / 2 = 3,825%). В данном случае как раз две выплаты в год. На величину процента не влияет рыночная цена бумаги, поскольку расчет ведется относительно номинала.
3. Текущая доходность
В этот показатель включается рыночная цена, упущенная в предыдущем случае: в реальности инвестор покупает бумагу на бирже по текущей рыночной стоимости. Покупка по цене ниже номинала даст дополнительную прибыль, покупка выше номинала снизит доходность. Об этой зависимости я писал здесь.
Формула расчета текущей доходности:
ТД = [Купон / Рыночная цена] × 100%
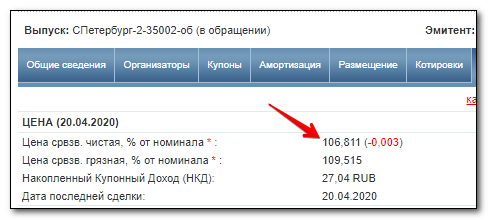
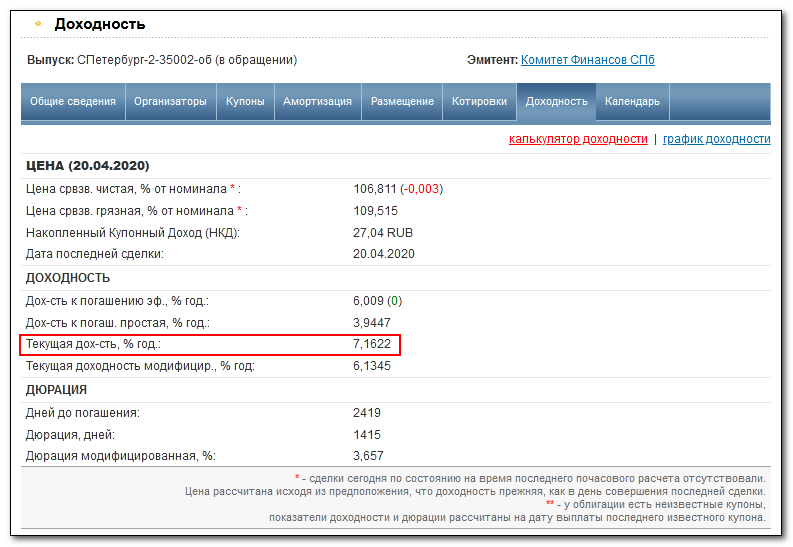
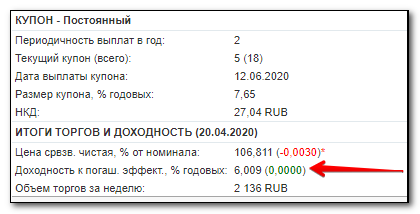
Облигация со ставкой 7,65% имеет купонный доход 76,5 руб. Но на сегодняшний день бумага продается с премией, т.е. дороже 100% от номинала:
Т.е. цена облигации равна не 1 000 руб., а 1 068,11 р. Расчет:
ТД = [76,5 / 1 068,11] × 100% = 7,162%
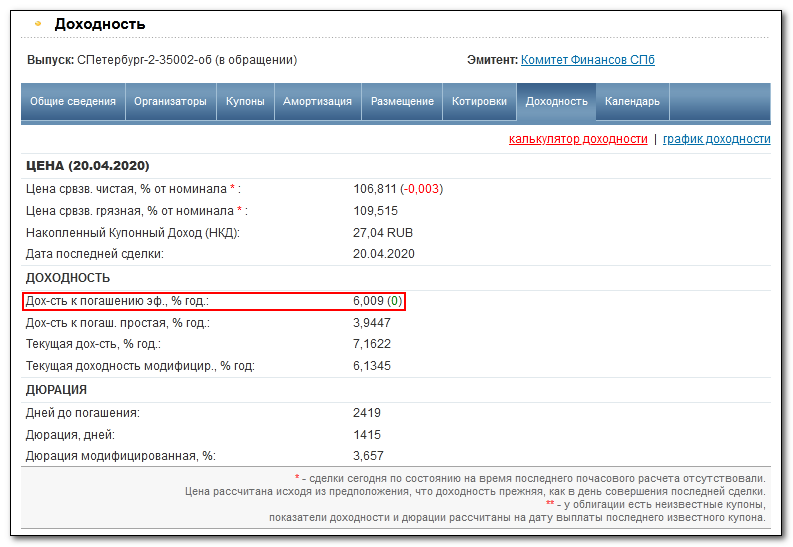
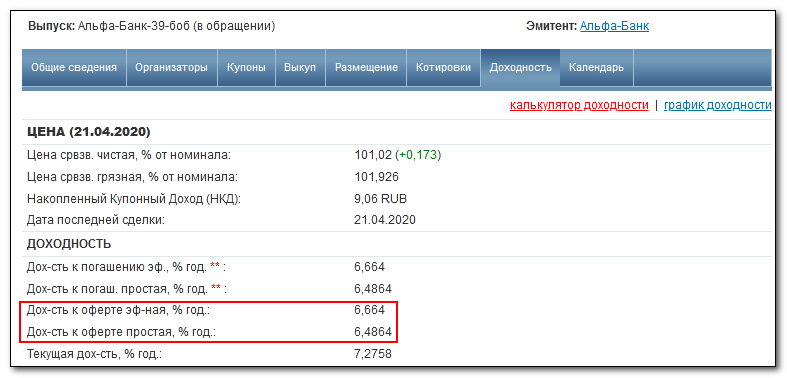
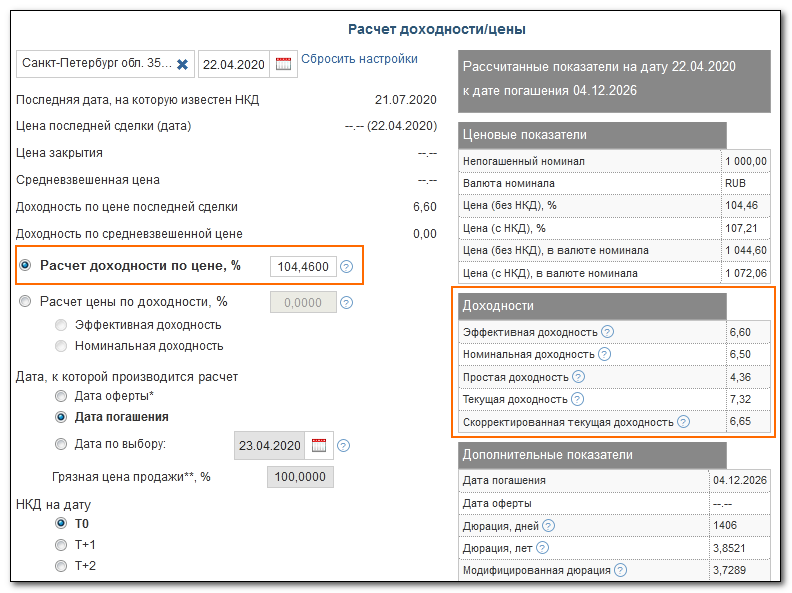
Текущая доходность меньше купонной, поскольку произошло удорожание облигации (покупка с премией). Увидеть эту доходность можно на вкладке в свойствах облигации:
4. Простая доходность к погашению
Наиболее часто для сравнения облигаций и понимания конечного результата используется простая и эффективная доходность к погашению. Что такое погашение – это завершение цикла ценной бумаги. К примеру, бонд имеет срок обращения 5 лет. Через 5 лет эмитент вернет держателю бумаги ее номинал, а сама облигация перестанет существовать.
Держать облигацию до погашения – частая практика. Инвесторы применяют ее, чтобы получить максимум купонного дохода и номинал. От номинала можно получить дополнительную выгоду, купив бумагу с дисконтом. Для расчета прибыли от удержания бонда с момента покупки до погашения и введен показатель простой доходности.
Формула расчета простой доходности к погашению:
Пояснение к формуле: выплаты купонов производятся с определенной периодичностью. Если инвестор продаст бумагу до выплаты, он вместе с рыночной ценой получит накопленный купонный доход (НКД) – проценты, которые накапливались за период удержания бумаги.
Например, бумага куплена за 1 000 руб. с тем же купонным доходом 7,65%. Выплаты производятся раз в год. Но инвестор продал облигацию через полгода владения и получил рыночную цену + 38,25 руб. (купон за 6 месяцев).
Новый покупатель получит весь купон в 76,5 руб., если удержит облигацию до выплаты процентов. В итоге его прибыль составит тоже 38,25. За год оба владельца – первый и второй – получат общий купон, разделенный пропорционально сроку владения.
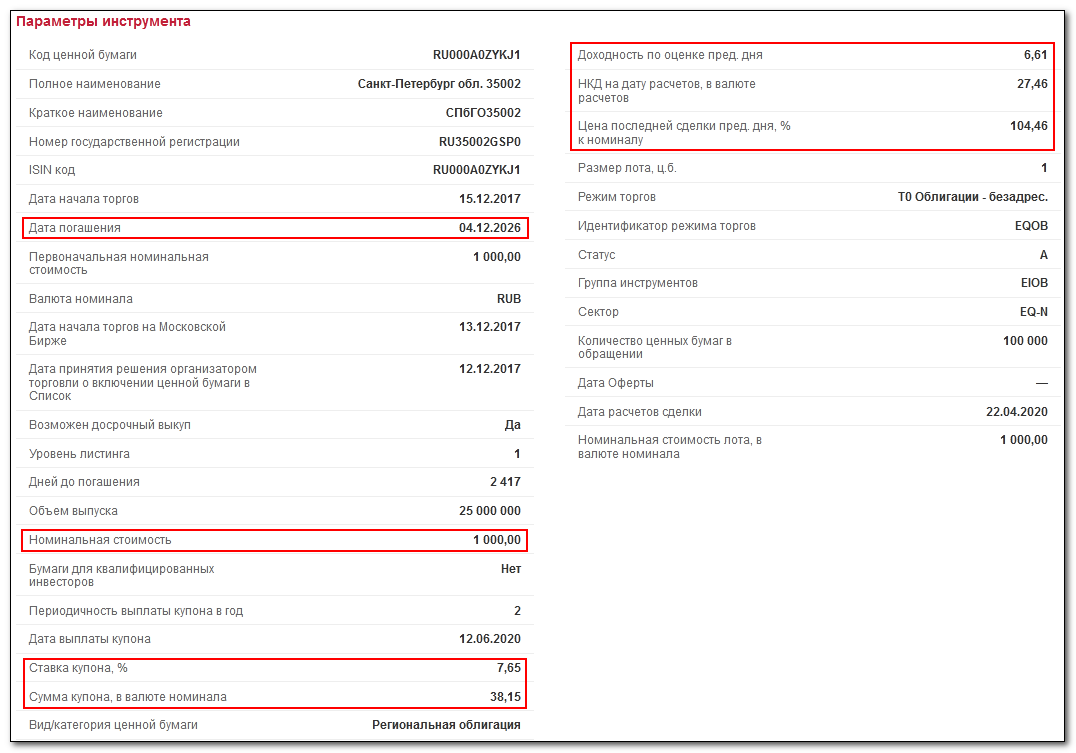
Данные для расчета:
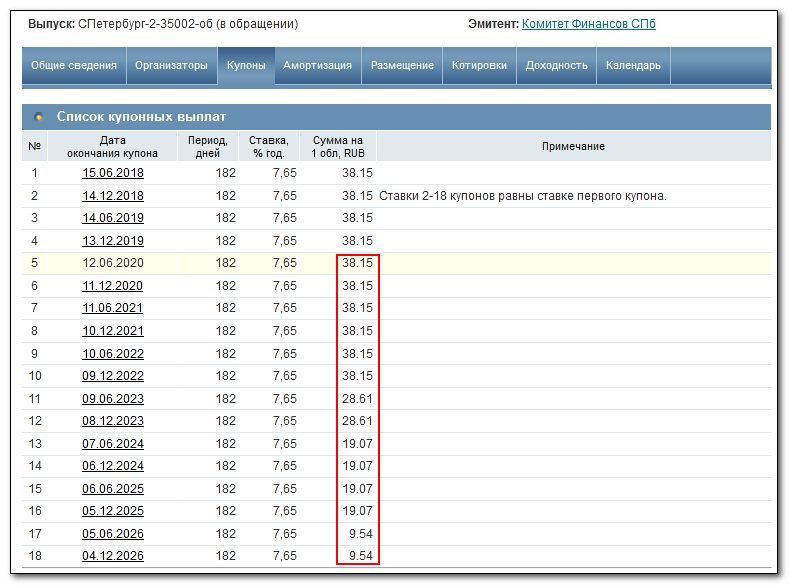
Все будущие купоны можно увидеть во вкладке «Купоны»:
Итого сумма купонов с текущего момента до погашения составляет 381.48 р. Расчет:
Доходность бонда при удержании до погашения с момента покупки (20.04.20) составит 3,94%. Полное погашение произойдет в декабре 2026 года. Это значение можно не считать самому — оно указывается в свойствах облигации:
✅ Формулу можно модифицировать, если продать облигацию до погашения — скажем, в апреле 2026 года. В этом случае купоны уменьшатся на две последние выплаты (9.54 × 2), а дни до погашения превратятся в число дней, которые инвестор удерживал облигацию. Вместо номинала нужно будет взять будущую рыночную цену + НКД (на апрель 2026), которые инвестор получит за продажу.
5. Эффективная доходность к погашению
Эффективная доходность к погашению, как и простая, показывает доход инвестора при удержании облигации с текущего момента до погашения – но в отличие от простой доходности, она предполагает реинвестирование всех полученных купонов в покупку тех же самых облигаций.
В результате эффективная доходность получается выше простой, причем разница тем больше, чем дольше обращается выпуск и чем больше купон. Понятно, что процедура актуальна для значительных сумм, которая позволяет купить новые облигации на полученные купоны. Можно сказать, что это рентабельность инвестиций инвестора.
Точная формула эффективной доходности довольно сложна и вычисляется из такой функции:
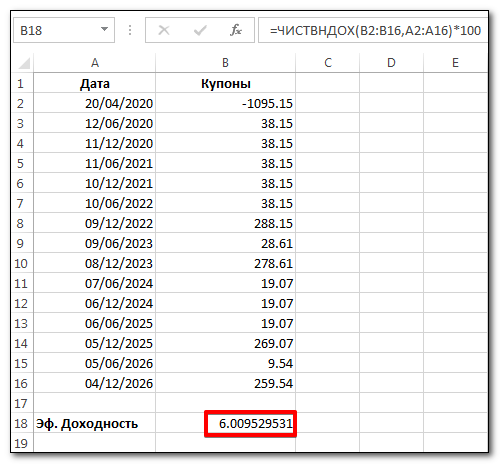
В Excel для расчета можно воспользоваться функцией ЧИСТВНДОХ, задав в первом столбце даты купонных выплат, а во втором — их значения в рублях. Если будете считать, то имейте в виду, что дату вида 20.04.2020 Excel может воспринять как текст и функция выдаст ошибку. Для случая выше:
Здесь первое значение (1095.15) это рыночная стоимость облигации с учетом НКД на дату покупки. Ставится со знаком «минус». Далее следуют выплачиваемые купоны, но с конца 2022 года начинается постепенный возврат номинала: четырьмя частями по 250 рублей. Это можно увидеть во вкладке «Амортизация». Поэтому эти суммы складываются с купонными выплатами, происходящими в тот же день. Результат полностью совпадает с данными rusbonds:
Кроме этого, можно воспользоваться и приближенным вариантом расчета, который как правило обеспечивает достаточную точность.
Формула хорошо подходит для равномерных купонных выплат с фиксированным доходом. Все данные для расчета таких облигаций нетрудно найти на том же rusbonds. Время, указанное в днях, следует разделить на 365.
Например, выпуск Альфа-Банк-002Р-03-боб имеет номинал 1000 рублей, текущую рыночную цену на 21.04.20 в размере 104.36% (1043.6 рубля), время до погашения 794 дня и сумму купонных выплат за год 92.26 р. Тогда
YTM = [((1000 – 1043.6)/(794/365) + 92.26) / (1000 + 1043.6) / 2] × 100% = 7,07% годовых
При этом rusbonds показывает для этой облигации эффективную доходность 7,12% в год, что очень близко.
Когда возникают проблемы при расчете доходности к погашению?
- Облигация является бессрочной;
- Купон облигации является переменным, т.е. заранее неизвестен
- Речь идет о фонде облигаций (см. далее)
Доходность к оферте
Оферта – это объявление заемщика (эмитента) о выкупе своих бондов:
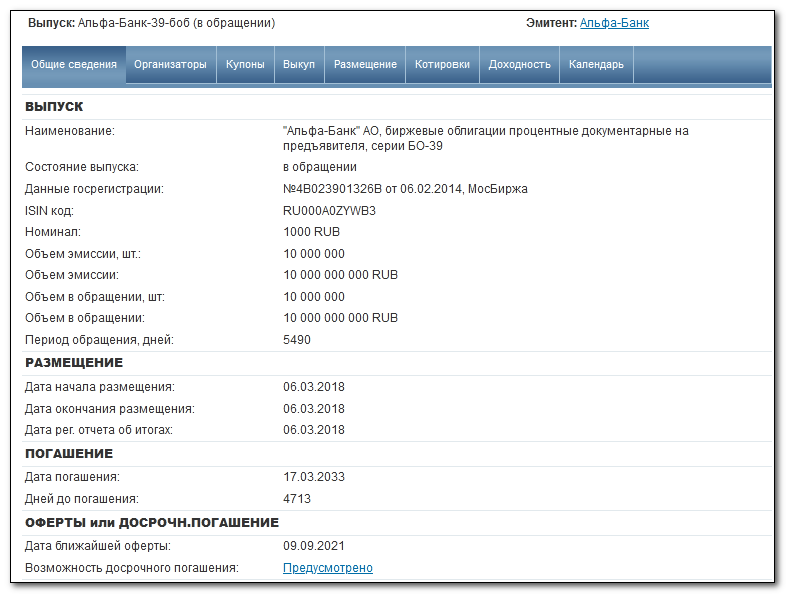
Зачем нужна оферта? Например, при понижении ключевой ставки эмитент должен продолжать платить по прежним выпускам более высокий купон — предусмотрев такую возможность, к облигации прилагается оферта с правом досрочного выкупа. После этого бумага может выйти из обращения — поэтому при наличии оферты доходность рассчитывается на ее дату. Пример:
Как видно, дата погашения установлена в марте 2033 года, однако есть и дата оферты, когда облигация может быть досрочно погашена. Поэтому во вкладке «Купоны» последняя выплата установлена 7 сентября 2021. В результате доходности рассчитываются на дату оферты аналогично случаям с погашением:
6. Номинальная доходность
Номинальная доходность редко используется в качестве оценки доходности облигаций. Более того, ее часто путают с купонной доходностью. Что она показывает? Фактически это эффективная доходность к погашению или оферте, нормированная на число купонов, выплачиваемых бондами в течение года.
Формула расчета номинальной доходности согласно Мосбирже:
Из формулы следует, что при n = 1 (одна купонная выплата в год) номинальная доходность купонной бумаги будет равна эффективной. Эффективное значение уже было рассчитано выше:
Частота выплат купонов в год у облигации Комфина равна 2. Тогда:
Доходность облигаций на сайте Мосбиржи
Данные по облигациям можно найти не только на сайте rusbonds. Источником может быть и сайт Московской биржи, где облигацию можно искать как по названию в поле поиска, так и используя ISIN-код. У рассмотренной выше облигации Комфина он RU000A0ZYKJ1. Данные по этому выпуску выглядят так:
Кроме того, можно увидеть график купонных выплат:
Итого, представлено достаточно данных для расчета — однако в данном случае нет указания, что облигация выпущена с амортизацией и следовательно номинал будет возвращаться частями.
Плюсом биржи является наличие калькулятора доходности, который доступен по ссылке https://www.moex.com/ru/bondization/calc . Для расчета нужно выбрать в поле сверху нужную облигацию и подставить ее рыночную цену (цена последней сделки предыдущего дня). В результате получается набор доходностей, совпадающих с данными rusbonds:
Доходность фондов облигаций
Отдельно стоит сказать про доходность фондов облигаций, торгующихся на бирже. Например, биржевых фондов ETF. Дело в том, что в этом случае паи фонда являются акциями с неизвестной ценой в любой момент будущего времени. Поэтому заранее просчитать доходность к погашению нельзя. Номинал у паев отсутствует, их покупатель не платит накопленный купонный доход — все уже включено в цену пая.
Если фонд стоил 30$, через год стоит 33$ и выплатил за это время 2$ в виде дивидендов (купонов), то доход инвестора равен (33-30+2)/30 = 16.7%. Если этот результат получился за N лет, то его нужно возвести в степень (1/N). Кстати, в сильный кризис фонды высокодоходных облигаций могут упасть на 20-30%, что даст отрицательный годовой результат. Несмотря на неопределенность дохода, я считаю этот способ лучшим для инвестиций в зарубежные облигации. Про общий расчет рыночной доходности читайте здесь.
Источник
Из чего состоит доход по облигации
Облигации — простой и надежный инвестиционный инструмент. Эти бумаги не испытывают сильной волатильности и имеют предсказуемый доход. Из чего складывается доход, как его рассчитать и получить максимальную выгоду — расскажем в этой статье.
Виды доходности по облигациям
Доход от актива формируется из двух составляющих:
- Купонных платежей, которые начисляются согласно процентной ставки на номинал.
- Цены облигации, которая может изменяться в зависимости от многих факторов, например экономической ситуации и надежности эмитента.
При ближайшем рассмотрении становится понятно, что существует множество других, менее очевидных показателей и оценок доходности, благодаря которым инвестор может сравнить активы и выбрать для себя наиболее выгодные.
Купонная
Называется еще ставкой купона. Показывает, какой процент от номинала бумаги эмитент выплатит вам за один год. Ставка устанавливается заранее и выплачивается с заданной периодичностью, чаще всего — раз в полгода.
ВАЖНО! Купонный доход начисляется каждый день, и инвестор сохранит его даже в том случае, если продаст бумагу до погашения.
Этот вид доходности интересен инвестору, который:
- купил бумагу по номиналу;
- бумага куплена сразу после выпуска;
- собирается держать актив до погашения;
- либо для дальнейших более сложных расчетов.
Текущая
Это показатель отношения купонных выплат за год к текущей цене облигации.
Имеет значение, если бумага куплена не более чем на полгода и будет продана задолго до погашения.
Простая к погашению
Учитывает не только купонный доход и стоимость покупки, но и цену погашения.
Необходимо принимать во внимание, когда актив куплен на длительный срок с намерением выводить и тратить купонную прибыль на неотложные нужды.
Эффективная к погашению
Наиболее полно и детально показывает прибыль владельца бумаги с учетом реинвестирования. Повышенная доходность возможна, если сохранять на брокерском счете все купонные платежи и на все эти средства докупать бумаги с аналогичным купоном.
Актуальна, если облигация куплена на длительный срок с намерением реинвестирования прибыли.
Доходность к продаже
Показатель, который поможет понять, нужно ли продавать облигацию, если ее цена изменилась. Причем делать это придется самому в ручном режиме.
Какие формулы используются при подсчете доходности бондов
Инвестору, который умеет просчитывать разные виды доходности, легче будет подбирать подходящие активы под себя в соответствии с поставленными целями и горизонтом инвестирования. А главное, этот навык поможет избежать потерь, ведь убыточные активы попадаются и среди облигаций!
Для подсчета существуют специальные формулы:
Накопленный купонный доход
НКД = С × t / 365, где
- С — сумма купонных выплат за год;
- t — число дней от начала купонного периода.
Например, инвестор купил бумагу ОФЗ номиналом 1000 ₽ со ставкой 4 % в год, что дает выплату 40 ₽ в год. Сделка проведена в 120-й день после покупки.
НКД = 40 × 120 / 365 = 13,15 ₽.
Текущая доходность
CY = Cг/P × 100 %, где
- Cг — купонные выплаты за год;
- P — цена актива.
Например, инвестор купил облигацию номиналом 1000 ₽ по цене 1050 ₽ и ставкой купона 4 %, то есть 40 ₽ в год.
CY = ( 40 / 1050) × 100 % = 3,8 % годовых.
Простая к погашению
Y = CY + N — P / P × 365 / t × 100 %, где
- CY — текущая доходность от купона;
- N — номинал актива;
- P — цена приобретения;
- t — время от покупки до погашения.
Например, инвестор купил двухлетнюю бумагу номиналом 1000 ₽ по цене 1050 ₽ со ставкой 4 % годовых и текущей доходностью 3,8 %.
Y = 3,8 % + ((1000 — 1050) / 1050) × 365 / 730 × 100 % = 1,42 % годовых.
Эффективная доходность к погашению
Рассчитывается по формуле.
YTMор = (N — P) / t + Cг / (N + P) / 2 × 100 %, где
- YTMор — доходность к погашению;
- Cг — сумма купонных выплат за год;
- P — текущая цена;
- N — номинал;
- t — лет до погашения.
Например, инвестор приобрел двухлетнюю облигацию номиналом 1000 ₽ по цене 1050 ₽ со ставкой 4 % годовых.
Ориентировочная эффективная доходность к погашению: YTM1 = ((1000 – 1050) / (730 / 365) + 40) / (1000 + 1050) / 2 × 100 % = 1,46 % годовых.
Доходность к продаже
Рассчитывается по той же формуле, но с новыми вводными.
Эмитенту подняли рейтинг через 30 дней после покупки облигации, в результате цена на нее выросла до 1075 ₽, после чего инвестор принял решение о ее продаже. Меняем в формуле номинал бумаги на цену продажи, а срок до погашения — на срок владения. Получаем простую доходность к продаже: Y = 3,8 % + ((1075 — 1050) / 1050) × 365 / 30 × 100 % = 32,8 % годовых.
ВАЖНО! Текущую, простую и эффективную доходности к погашению можно легко рассчитать с помощью облигационного калькулятора доходности, который можно найти, например, на сайте Мосбиржи.
Как получить максимальный доход
Чтобы получить наибольшую выгоду, можно действовать разными способами, в том числе с учетом доходности.
- Например, если нужно увеличить купонный доход, нужно выбирать бумаги с наибольшим процентным значением купона, желательно выше 8 %. Надо отметить, что наиболее надежные ОФЗ таких значений не предлагают, значит придется рисковать.
- Чтобы увеличить текущую доходность, надо постараться купить бумагу значительно дешевле номинала. При удачной покупке инвестор обязательно окажется в выгоде.
- Поднять доход простой к погашению можно, если держать долговой актив от покупки до погашения. Таким образом можно вернуть и номинал, и все купонные выплаты, значительно увеличив прибыль.
- Сделать вложения наиболее эффективными можно, если реинвестировать всю прибыль в новые облигации.
Доходность облигации — важнейший параметр ценной бумаги, от этого зависит цена актива, а значит, и прибыль, которую может получить инвестор. Однако, стремясь к повышению доходности, нельзя забывать о надежности эмитента, чтобы в погоне за прибылью не потерять больше.
Подпишитесь на нашу рассылку, и каждое утро в вашем почтовом ящике будет актуальная информация по всем рынкам.
Источник