Распределения вероятностей и ожидаемая доходность
Поскольку риск связан с вероятностью того, что фактическая доходность будет ниже ее ожидаемого значения, распределения вероятностей являются основой для измерения риска. Предположим, например, что вы финансовый менеджер фирмы, которая решила инвестировать 100 000 долларов сроком на один год. В таблице 1 приведены четыре альтернативных варианта инвестиций:
1. Казначейские векселя (Т-векселя) со сроком погашения один год и ставкой дохода 8%, которые могут быть приобретены с дисконтом (т.е. по цене ниже номинала); в момент погашения будет выплачена их номинальная стоимость.
2. Корпорационные облигации, которые продаются по номиналу с купонной ставкой 9% (т.е. на 100 000 долларов вложенного капитала можно получать 9000 долларов годовых) и сроком погашения 10 лет. Однако ваша фирма планирует продать эти облигации в конце первого года. Следовательно, фактическая доходность по облигациям будет зависеть от уровня процентных ставок на конец года. Этот уровень в свою очередь зависит от состояния экономики на конец года: быстрые темпы экономического развития, вероятно, вызовут повышение процентных ставок, что снизит рыночную стоимость облигаций, в случае экономического спада возможна противоположная ситуация.
3. Проект капиталовложений №1, чистая стоимость которого составляет 100 000 долларов. Денежный поток в течение года равен нулю, все выплаты осуществляются в конце года. Сумма этих выплат зависит от состояния экономики.
4. Альтернативный проект капиталовложений №2, совпадающий по всем параметрам с проектом №1 и отличающийся от него лишь распределением вероятностей ожидаемых в конце года выплат.
Распределением вероятностей называется множество возможных исходов с указанием вероятности появления каждого из них. Таким образом, в таблице 1 представлены четыре распределения вероятностей, соответствующие четырем альтернативным вариантам инвестирования. Доходность по казначейским векселям точно известна — она составляет 8% и не зависит от состояния экономики. Таким образом, риск по казначейским векселям равен нулю.
Отметим, что инвестиции в казначейские векселя являются безрисковыми только в том смысле, что их номинальная доходность не изменяется в течение данного периода времени. Реальная же доходность казначейских векселей содержит определенную долю риска, поскольку она зависит от фактических темпов роста инфляции в течение периода владения векселями. Более того, казначейские векселя могут представлять проблему для инвестора, который обладает портфелем ценных бумаг с целью получения непрерывного дохода: когда истекает срок платежа по казначейским векселям, необходимо осуществить реинвестирование денежных средств и если процентные ставки снижаются, доход портфеля также уменьшится.
Этот вид риска, который носит название риска нормы реинвестирования, не учитывается в нашем примере, так как период, в течение которого фирма владеет векселями, соответствует сроку их погашения. Наконец, отметим, что релевантная доходность любых инвестиций — это доходность после уплаты налогов, поэтому, значения доходности, используемые для принятия решения, должны отражать доход за вычетом налогов.
По трем другим вариантам инвестирования реальные, или фактические, значения доходности не будут известны до окончания соответствующих периодов владения активами. Поскольку значения доходности не известны с полной определенностью, эти три вида инвестиций являются рисковыми.
Оценка доходности по четырем инвестиционным альтернативам
| Таблица 1 | |||||
| Доходность инвестиций при данном состояния экономики, % | |||||
| Состояние экономики | Вероятность | Казначейские векселя, % | корпорационные облигации | проект №1 | проект №2 |
| Глубокий спад | 0,05 | 80 | 12,0 | — 3,0 | — 2,0 |
| Незначительный спад | 0,20 | 80 | 10,0 | 6,0 | 9,0 |
| Стагнация | 0,5 | 80 | 9,0 | 11,0 | 12,0 |
| Незначительный подъем | 0,20 | 80 | 8,5 | 14,0 | 15,0 |
| Сильный подъем | 0,05 | 80 | 8,0 | 19,3 | 26,0 |
| ____________________________________________________________________________________ | |||||
| Ожидаемая доходность | — | 80 | 9,2 | 10,3 | 12,0 |
Примечание. Доходность, соответствующую различным состояниям экономики следует рассматривать как интервал значений, а отдельные ее значения — как точки внутри этого интервала. Например, 10%-ная доходность облигации корпорации при незначительном спаде представляет собой наиболее вероятное значение доходности при данном состоянии экономики, а точечное значение используется для удобства расчетов.
Распределения вероятностей бывают дискретными или непрерывными. Дискретное распределение вероятностей имеет конечное число исходов; так, в таблице 1 приведены дискретные распределения вероятностей. Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов. Каждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облигаций составит 9%, равна 0.50.
Если умножить каждый исход на вероятность его появления, а затем сложить полученные результаты, мы получим средневзвешенную исходов. Весами служат соответствующие вероятности, а средневзвешенная представляет собой ожидаемое значение. Так как исходами являются доходности, ожидаемое значение — это ожидаемая доходность (expected rate of return, k), которую можно представить в следующем виде:
, где
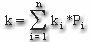
ki — i-й возможный исход,
Рi — вероятность появления i-го исхода,
n — число возможных исходов.
Используя формулу, находим, что ожидаемая доходность проекта 2 равна 12.0%
к = -2.0% * 0.05 + 9.0% * 0.20 + 12.0% * 0.50 + 15%* 0.20 + 26.0% * 0.05 = 12.0%
Ожидаемые доходности трех других альтернативных вариантов инвестирования найдены аналогичным образом (таблице 1).
Дискретные распределения вероятностей могут быть представлены графически или в табличной форме. На рисунке 1 приведены столбиковые диаграммы (или гистограммы) проектов №1 и №2.
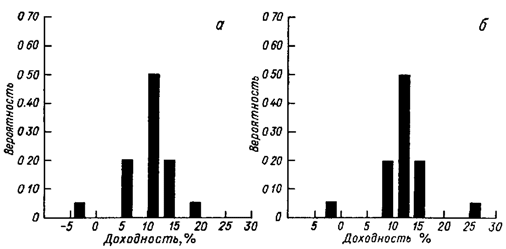
Рисунок 1. Графическое представление дискретного распределения вероятностей; а — проект №1; б — проект №2
Возможные значения доходности проекта №1 принадлежат промежутку от -3.0 до +19.0%, а проекта №2 от -2.0 до +26.0%. Отметим, что высота каждого столбца представляет собой вероятность появления соответствующего исхода, а сумма этих вероятностей по каждому варианту равна 1.00. Отметим также, что распределение значений доходности проекта №2 симметрично, тогда как соответствующее распределение для проекта №1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначейских векселей представлена единственным столбцом, а доходность корпорационных облигаций представлена диаграммой, имеющей правостороннюю асимметрию.
Программная реализация данной методики финансовой математики сделана в: «Альтаир Финансовый калькулятор 2.xx».
На примере расчета ожидаемой доходности можно увидеть, как применять программу «Альтаир Финансовый калькулятор 2.xx» на практике.
Главная 
Методики финансового и инвестиционного анализа Финансовая математика Производительность труда
Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.
Источник
10.8. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ДОХОДНОСТИ
Рассмотрим некую компанию Genco. Предположим, вы покупаете акции Genco Corporation по цене 100 долл. за акцию и намереваетесь владеть ими в течение года. Как уже рассказывалось в главе 2, совокупную ставку доходности (или просто доходность) можно представить как сумму двух компонентов: дивидендной доходности и доходности в результате изменения курса акций:
_ Выплаченные дивиденды (Конечная цена акции — Начальная цена) Начальная цена Начальная цена г = Дивидендный компонент доходности + Ценовой компонент доходности
Предположим, что купив акции Genco, вы рассчитываете, что дивидендный ком понент будет равен 3%, ценовой компонент составит 7%, так что ожидаемая ставка доходности будет равняться 10%.
Широко используемая единица измерения рискованности активов (в частности, акций Genco) — это изменчивость (volatility) . Изменчивость связана с диапазоном возможных ставок доходности акций и вероятностью их получения. Чем шире диапазон между возможными показателями доходности и чем больше вероятность получения экстремальных значении, тем выше показатель изменчивости акции. Например, если вас попросят дать «точечную оценку» доходности акций Genco в следующем году, то ваш ответ будет 10%. При этом вы не удивитесь, если окажется, что реальная доходность оказалась больше или меньше предсказанной вами. Доходность может быть как очень низкой (-50%), так и очень высокой (+80%). Чем сильнее расхождение между возможными показателями доходности, тем сильнее изменчивость. Чтобы лучше понять суть изменчивости, давайте рассмотрим распределение вероятностей получения разных уровней доходности для акций Genco. Всем возможным уровням доходности соответствуют вероятности от нуля (полное отсутствие вероятности достижения этого уровня) до единицы (данная доходность будет получена обязательно).
Предположим, что нам абсолютно точно известно, что в будущем году доходность составит 10%.
Таблица 10.1. Распределение вероятностей ставок доходностеай
Состояние экономики Ставка доходности акций Оепсо Вероятное
Подъем 30% 020 Нормальное 10% 0,60 Спад -10% 0.20
Распределение вероятности в табл. 10.1 означает, что если вы вложите деньги в акции Genco, то получите, скорее всего, 10%-ную доходность. Вероятность этого в три раза превышает вероятность получения двух других значений доходности — 10% и 30%.
Ожидаемая ставка доходности (expected rate of return) (среднее значение доходности) определяется как сумма всех возможных ставок доходности, умноженных на соответствующую вероятность их получения: (10.1)
Применив эту формулу к рассматриваемому случаю, мы обнаружим, что ожидаемая ставка доходности акций Genco равна
Е(г) =0,2х30% +0,6х10% +0,2х210% =10%
-10 10 30 Доходность
Рис. 10.1. Распределение вероятностей доходности акций Сепсо
Очевидно, в этом случае вы сильнее сомневаетесь в том, какой же будет ставка доходности, чем в случае полной определенности. А теперь рассмотрим другой пример, акции некой компании Risco, у которой диапазон вероятностных показателей доходности еще шире, чем у Сепсо. Распределение вероятности Risco сравнивается с распределением вероятности Сепсо в табл. 10.2 и на рис. 10.2.
!Таблица 10.2. Распределение вероятностей доходности акций А^со и Оепсо !Ц Состояние Подъем Нормальное Спад
Ставка доходности акций Ставка доходности акций Вероятнос
Рис. 10.2. Распределение вероятностей доходности акций Genco и Risco
Обратите внимание, что показатели вероятности одинаковы для обеих акций но • Risco более широкий диапазон колебаний доходности. Если экономика будет находиться на подъеме, Risco принесет своим акционерам 50% доходности (а Genco толью 30%). Но если экономическое положение ухудшится, доходность Risco упадет до -30% а Genco до -10%. Другими словами, показатели доходности инвестиций в акции Risa изменяются более сильно.
Источник
Распределение доходностей на рынке акций
Автор: Дмитрий Никитенко
Дата записи
Сегодня мы разберем очень интересную тему о распределении доходностей акций. Она раскрывает природу инвестиционного риска ещё глубже и позволяет лучше понять как именно работает фондовый рынок и чего от него следует ожидать.
Если вы ещё не читали статью про инвестиционный риск, стоит сначала прочитать в ней про стандартное отклонение.
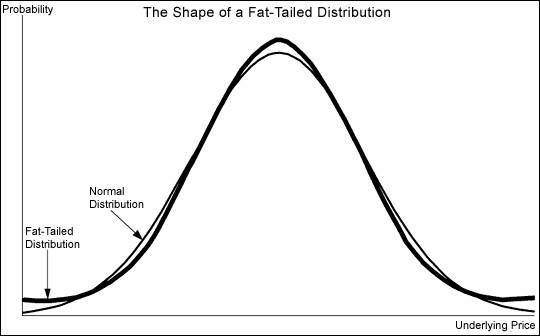
Распределение доходностей на фондовых рынках принято сравнивать с кривой нормального распределения (по функции Гаусса). Хотя далее мы выясним, что реальное распределение доходностей не полностью соответствует этой кривой, она весьма неплохо описывает происходящее на рынке на длинных периодах времени.
Кривая нормального распределения. По оси X – стандартное отклонение, по оси Y – вероятность. Проценты – это частота попадания значения стандартного отклонения в закрашенную область под кривой. Источник: Википедия
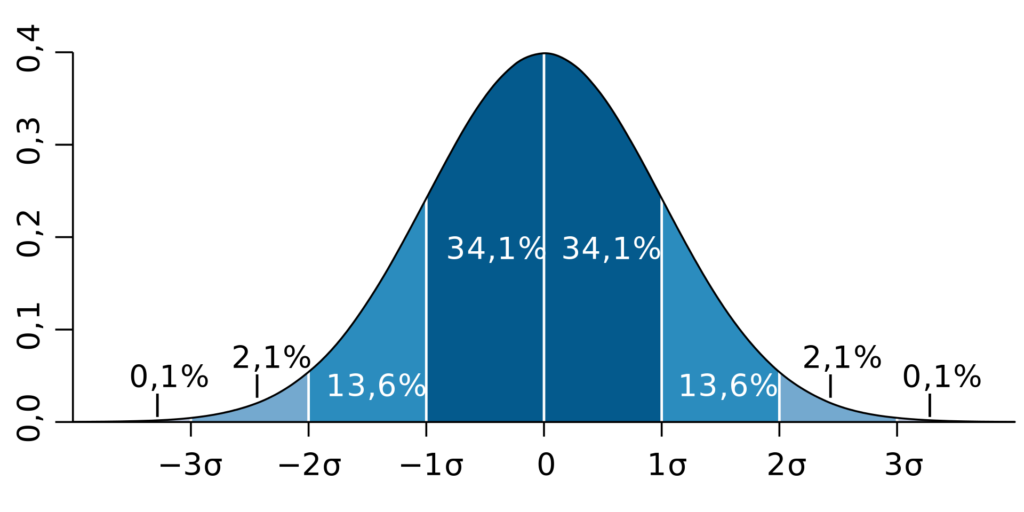
Смысл нормального распределения заключается в том, что основная часть значений случайной величины концентрируется возле своей средней (математического ожидания случайной величины), а значения по краям кривой маловероятны (случаются редко). Так, чем больше стандартное отклонение значений от среднего, тем меньше вероятность их появления.
В статистике существует правило трёх сигм (стандартных отклонений), которое наглядно изображено на графике выше. Закрашенные на нём области под кривой показывают сколько процентов времени стандартное отклонение значений случайной величины не превышает одну, две или три сигмы. Значения с отклонением более трёх сигм считаются практически невозможными.
Чтобы проверить соблюдается ли нормальное распределение доходностей на рынке акций, возьмем полные (с дивидендами) реальные (выше инфляции) доходности акций США на периоде с 1871 по 2018 год (по данным Роберта Шиллера и Yahoo! Finance):
- среднее арифметическое этих доходностей составило 8.5%;
- стандартное отклонение = 18.5%.
Если бы кривая нормального распределения полностью описывала распределение доходностей на фондовом рынке, то, согласно правилу трёх сигм:
- 68.27% времени доходность была бы между средним арифметическим ± одно стандартное отклонение (-10% и 27%);
- 95.45% времени – между средним ± два стандартных отклонения (-28.5% и 45.5%);
- 99.73% времени – между средним ± три стандартных отклонения (-47% и 64%).
Наблюдение за реальными данными даёт хоть и похожий, но всё же отличающийся результат. На самом деле доходности рынка акций США выше инфляции за 148 лет укладывались:
- в одно стандартное отклонение от своей средней арифметической 67.57% времени (не 68.27%);
- в два стандартных отклонения – 93.92% времени (не 95.45%);
- в три стандартных отклонения – 100% времени (не 99.7%), значений за пределами -47% и 64% за этот период не было, минимальная и максимальная доходность составили -38.47% в 1931 году и 57.16% в 1954 году.
Получается, что 9 из 148 лет принесли доходность меньше -28.49% или больше 45.51% (двух стандартных отклонений), что составило 6.08% случаев, а не ожидаемые согласно нормальному распределению 100% — 95.45% = 4.55%. Разница не так велика, но она есть и говорит о том, что аномальные доходности на рынке акций немного более вероятны, чем предсказывает нормальное распределение.
Посмотрим на те же данные по США на графике распределения доходностей. Здесь и далее снова используются полные реальные годовые доходности, разделенные на интервалы по 10%, каждый год определен в свой интервал.
Источники данных: Robert Shiller, Yahoo! Finance; инфляция: Robert Shiller, Bureau of Labor Statistics
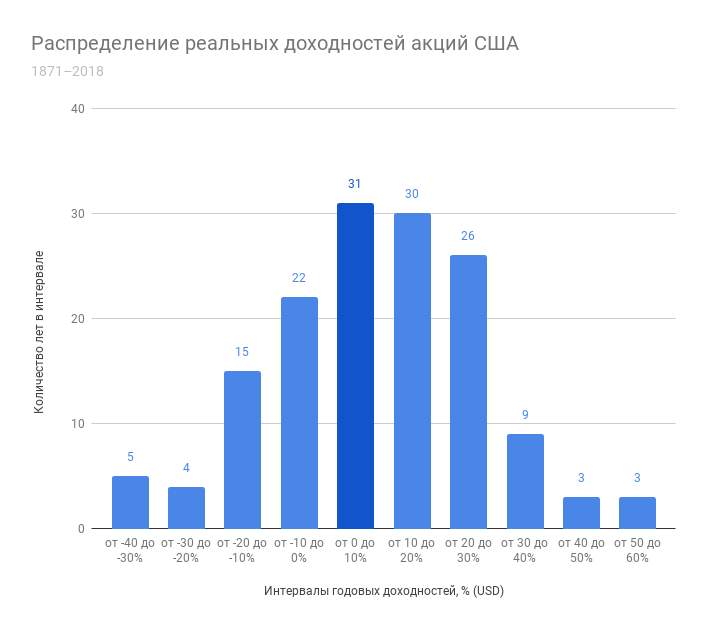
График напоминает кривую нормального распределения, однако, крайних значений немного больше, чем предполагает гауссиана, а значит они случаются чаще. Интервал от -40 до -30% содержит в себе 5 лет, что больше, чем у предыдущего интервала от -30 до -20% (4 года), а интервал от 50 до 60% содержит в себе столько же лет (3), сколько и предыдущий, хотя согласно нормальному распределению тоже должен быть меньше.
Это называется fat tail или толстый хвост кривой – вместо того, чтобы стремиться к оси абсцисс (к нулю), кривая может отрываться от неё, что не соответствует нормальному распределению. Крупные просадки или аномально высокие доходности не настолько маловероятны как предсказывает гауссиана, что получило название tail risk. Такое поведение рынка подчёркивает важность психологии в инвестировании и умения инвестора пережидать плохие годы, не продавая активы. Каким бы плохим не был отдельно взятый день или год, доходность акций и облигаций имеет положительное математическое ожидание (среднее значение), а значит время и сложный процент сделают своё дело.
Используя индекс полной доходности MSCI World Net я также построил график распределения реальных годовых доходностей акций развитых стран. Хотя доступная выборка по нему значительно меньше (с 1970 года), можно отметить сходство в количестве положительных периодов с акциями США – практически 70% времени он приносил положительную реальную доходность. Об особенностях распределения на этом периоде я говорить не буду – довольно маленькое число наблюдений. Здесь худшим годом для индекса стал 2008 – доходность едва опустилась за -40% с учетом инфляции, а лучшим – 1986 с практически такой же доходностью, но без минуса.
График: Capital-Gain.ru. Источники данных: MSCI World Net Index; инфляция: Bureau of Labor Statistics
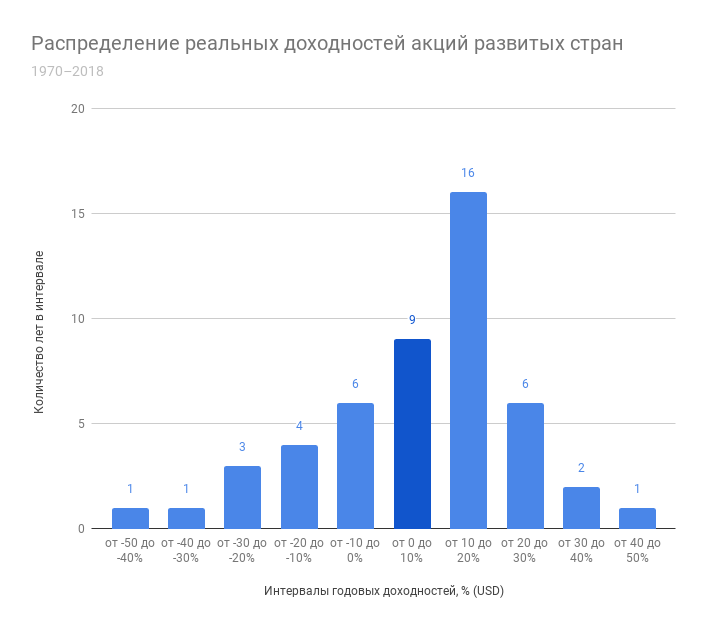
И, наконец, давайте посмотрим на распределение месячных доходностей на рынке акций США с 1988 года (375 месяцев).
График: Capital-Gain.ru. Источник данных: Yahoo! Finance
Здесь тоже можно заметить аномальные доходности по краям (больше ±10% за один месяц — это сильно). Но что ещё общего можно заметить на этих графиках? Они все немного сдвинуты вправо по оси доходностей, можно сказать, имеют больший вес в своей положительной части. Это является свидетельством того, что доходность акций исторически имела положительное математическое ожидание. По сути мы видим здесь ту добавленную стоимость, что генерирует бизнес по всему миру.
Нассим Николас Талеб в своей книге «Черный лебедь» пишет, что нормальное распределение отлично подходит для описания физически ограниченных значений (например, рост человека), потому что они не масштабируются так сильно, как физически неограниченные (например, продажи бестселлера или доходность фондового рынка). Конечно, ни продажи, ни доходность не могут быть бесконечными, однако, вы с гораздо меньшей вероятностью встретите человека ростом 3 метра, чем неожиданно проданную огромным тиражом книгу или аномальную доходность на рынке. Такие из ряда вон выходящие события он называет черными и белыми лебедями (в зависимости от того негативный оно имеет смысл или позитивный). Тут стоит отметить, что, на мой взгляд и по результатам самостоятельного анализа данных, как нормальное распределение не описывает доходности на фондовом рынке полностью, так и Талеб в своей книге преувеличивает значимость этих отклонений от нормального распределения , если смотреть на них с точки зрения долгосрочного инвестора. Для трейдеров, впрочем, эти отклонения действительно могут быть гораздо более значительными, ведь они оперируют более короткими временными интервалами, на которых аномальные (для правила трёх сигм) доходности случаются чаще – в дневных и месячных данных появляются стандартные отклонения и больше трёх сигм, что по нормальному распределению практически невозможно. К тому же трейдеры могут автоматически фиксировать убытки с помощью биржевых заявок стоп лосс, которые не применяются пассивными портфельными инвесторами.
Популярным примером является черный понедельник 19 октября 1987 года, когда индекс Dow Jones за один день упал на 22.61% – 25 своих дневных стандартных отклонений (!). Более недавний пример, изображенный на графике ниже – 24 июня 2016 года, когда состоялся референдум о Брексите и некоторые активы продемонстрировали аномальную дневную доходность. Количество лет в последней колонке таблицы, которые, согласно нормальному распределению, надо подождать, чтобы увидеть такие дневные доходности, намекает нам, что они гораздо более вероятны, чем может предсказать кривая Гаусса.
Доходности инструментов в день референдума в Великобритании, их множитель СКО и количество лет, раз в которые они ожидаются согласно нормальному распределению вероятностей. Источник: Charlie Bilello
Несмотря на то, что аномальные доходности на фондовом рынке – не такая редкость, как может спрогнозировать кривая нормального распределения, долгосрочному инвестору не стоит обращать внимания на них и уж тем более продавать свои активы из-за плохих новостей, фиксируя убыток , потому что такие аномальные доходности встречаются чаще именно на дневных или месячных данных, чем на годовых. Картинка ниже вполне подтверждает выделенные в этой статье утверждения – плохие новости или нет, положительная ожидаемая доходность и сложный процент долгосрочно заставляют капитал расти.
Прирост капитала, вложенного в акции компаний малой капитализации (small stocks), крупной капитализации (large stocks), государственные облигации (government bonds), векселя (treasury bills) и инфляция. Источник: SeekingAlpha
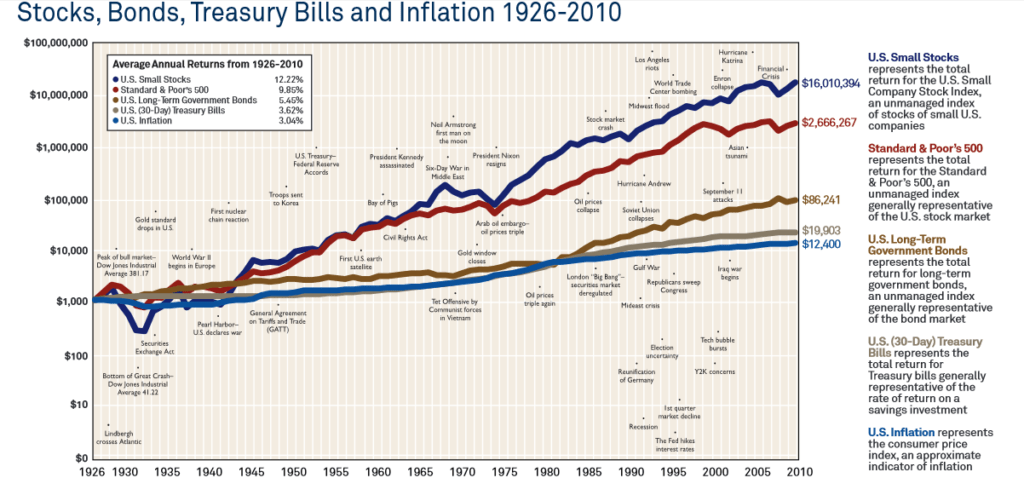
На выше графике показаны события, которые повлияли на рынок. Как видите, несмотря на войны и кризисы, активы показали значимый прирост капитала, опережающий инфляцию. Другой популярный пример против торговли по новостям показывает, как часто СМИ ошибаются в своих прогнозах.
График индекса акций США S&P 500 и новостные заголовки. Источник: Barry Ritholtz
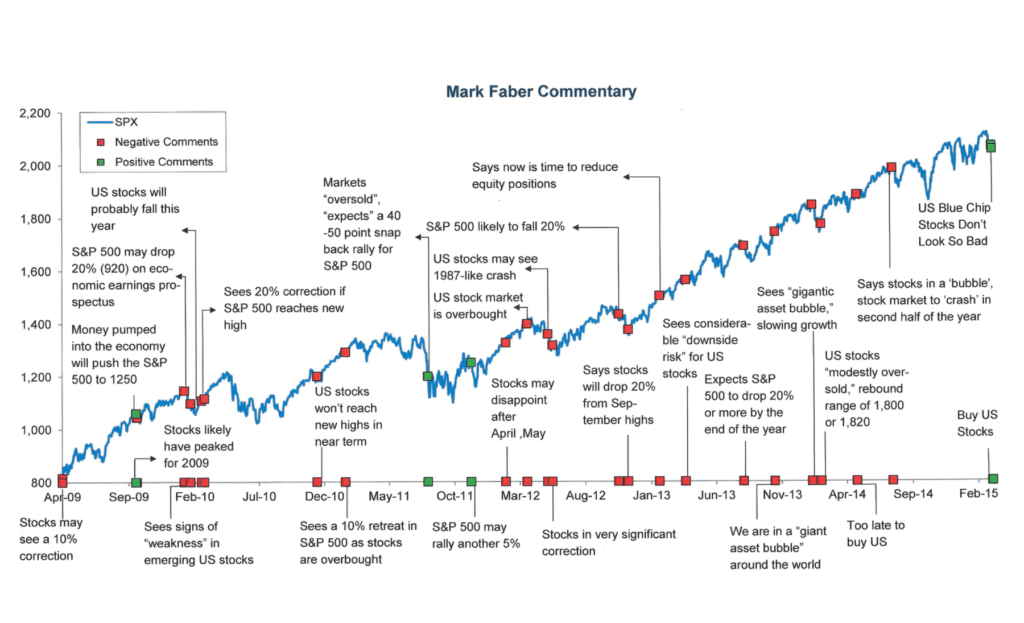
Комиссии и распределение доходностей
На новости мы повлиять не можем, зато вполне возможно повлиять на комиссии и налоги, которые инвестор платит фондам, брокерам и государству. Чем больше размер комиссий и налогов, тем меньше математическое ожидание доходности портфеля, а значит и распределение его доходностей на графике смещается влево на размер комиссий и налогов – ближе к отрицательной зоне. Схематично это показано на графике ниже.
Влияние комиссий и налогов на распределение доходностей. Источник: Vanguard
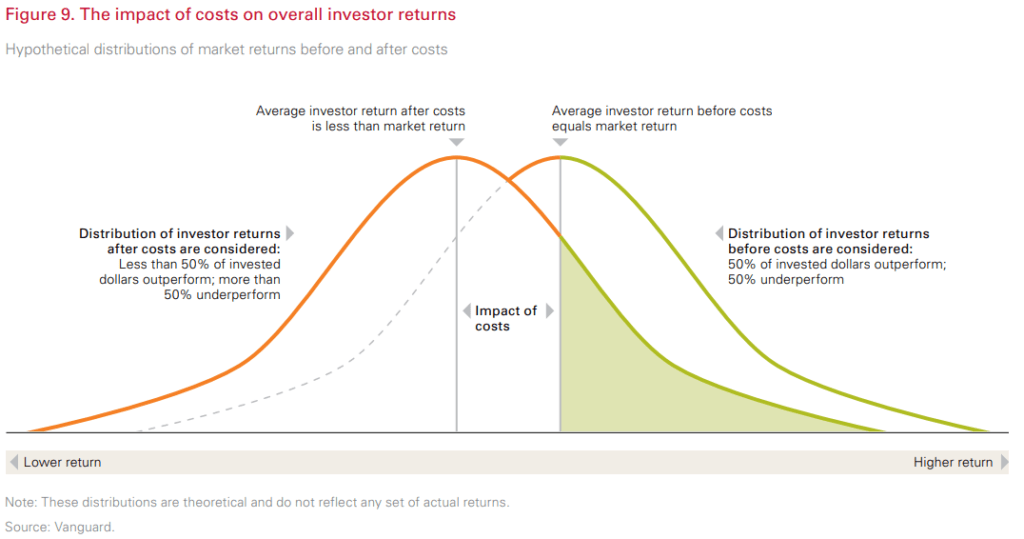
Долгосрочному пассивному инвестору гораздо полезнее думать о том как уменьшить свои комиссии и воспользоваться налоговыми льготами, чем о новостях и аномалиях на фондовом рынке.
Источник