Вероятность наступления события доходность

Ожидаемая доходность акций

В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.

Формула

В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

(1)

где P_i – вероятность наступления i-го исхода событий;

k_i – доходность при i-ом исходе событий;

n – количество исходов событий.

В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

(2)

k_i – доходность ценной бумаги в i-ом периоде;

n – количество наблюдений.

Пример расчета

Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.

Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.

_А = 0,25*18+0,5*12+0,25*3 = 11,25%

_Б = 0,3*22+0,45*14+0,25*(-2) = 12,4%

_В = 0,2*35+0,45*17+0,35*(-5) = 12,9%

Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.

Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.

Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.

_А = (-2,3+7+4,1-3,4+6,2+4,5+1,8)/7 = 2,56%

_Б = (4,1-5,7+2,4+4,8-1,2+1,1+0,3)/7 = 0,83%

_В = 0,2*35+0,45*17+0,35*(-5) = 0,64%

Источник

Распределения вероятностей и ожидаемая доходность

Поскольку риск связан с вероятностью того, что фактическая доходность будет ниже ее ожидаемого значения, распределения вероятностей являются основой для измерения риска. Предположим, например, что вы финансовый менеджер фирмы, которая решила инвестировать 100 000 долларов сроком на один год. В таблице 1 приведены четыре альтернативных варианта инвестиций:

1. Казначейские векселя (Т-векселя) со сроком погашения один год и ставкой дохода 8%, которые могут быть приобретены с дисконтом (т.е. по цене ниже номинала); в момент погашения будет выплачена их номинальная стоимость.

2. Корпорационные облигации, которые продаются по номиналу с купонной ставкой 9% (т.е. на 100 000 долларов вложенного капитала можно получать 9000 долларов годовых) и сроком погашения 10 лет. Однако ваша фирма планирует продать эти облигации в конце первого года. Следовательно, фактическая доходность по облигациям будет зависеть от уровня процентных ставок на конец года. Этот уровень в свою очередь зависит от состояния экономики на конец года: быстрые темпы экономического развития, вероятно, вызовут повышение процентных ставок, что снизит рыночную стоимость облигаций, в случае экономического спада возможна противоположная ситуация.

3. Проект капиталовложений №1, чистая стоимость которого составляет 100 000 долларов. Денежный поток в течение года равен нулю, все выплаты осуществляются в конце года. Сумма этих выплат зависит от состояния экономики.

4. Альтернативный проект капиталовложений №2, совпадающий по всем параметрам с проектом №1 и отличающийся от него лишь распределением вероятностей ожидаемых в конце года выплат.

Распределением вероятностей называется множество возможных исходов с указанием вероятности появления каждого из них. Таким образом, в таблице 1 представлены четыре распределения вероятностей, соответствующие четырем альтернативным вариантам инвестирования. Доходность по казначейским векселям точно известна — она составляет 8% и не зависит от состояния экономики. Таким образом, риск по казначейским векселям равен нулю.

Отметим, что инвестиции в казначейские векселя являются безрисковыми только в том смысле, что их номинальная доходность не изменяется в течение данного периода времени. Реальная же доходность казначейских векселей содержит определенную долю риска, поскольку она зависит от фактических темпов роста инфляции в течение периода владения векселями. Более того, казначейские векселя могут представлять проблему для инвестора, который обладает портфелем ценных бумаг с целью получения непрерывного дохода: когда истекает срок платежа по казначейским векселям, необходимо осуществить реинвестирование денежных средств и если процентные ставки снижаются, доход портфеля также уменьшится.

Этот вид риска, который носит название риска нормы реинвестирования, не учитывается в нашем примере, так как период, в течение которого фирма владеет векселями, соответствует сроку их погашения. Наконец, отметим, что релевантная доходность любых инвестиций — это доходность после уплаты налогов, поэтому, значения доходности, используемые для принятия решения, должны отражать доход за вычетом налогов.

По трем другим вариантам инвестирования реальные, или фактические, значения доходности не будут известны до окончания соответствующих периодов владения активами. Поскольку значения доходности не известны с полной определенностью, эти три вида инвестиций являются рисковыми.

Оценка доходности по четырем инвестиционным альтернативам

Таблица 1
Доходность инвестиций при данном состояния экономики, %
Состояние экономики	Вероятность	Казначейские векселя, %	корпорационные облигации	проект №1	проект №2
Глубокий спад	0,05	80	12,0	— 3,0	— 2,0
Незначительный спад	0,20	80	10,0	6,0	9,0
Стагнация	0,5	80	9,0	11,0	12,0
Незначительный подъем	0,20	80	8,5	14,0	15,0
Сильный подъем	0,05	80	8,0	19,3	26,0
____________________________________________________________________________________
Ожидаемая доходность	—	80	9,2	10,3	12,0

Примечание. Доходность, соответствующую различным состояниям экономики следует рассматривать как интервал значений, а отдельные ее значения — как точки внутри этого интервала. Например, 10%-ная доходность облигации корпорации при незначительном спаде представляет собой наиболее вероятное значение доходности при данном состоянии экономики, а точечное значение используется для удобства расчетов.

Распределения вероятностей бывают дискретными или непрерывными. Дискретное распределение вероятностей имеет конечное число исходов; так, в таблице 1 приведены дискретные распределения вероятностей. Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов. Каждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облигаций составит 9%, равна 0.50.

Если умножить каждый исход на вероятность его появления, а затем сложить полученные результаты, мы получим средневзвешенную исходов. Весами служат соответствующие вероятности, а средневзвешенная представляет собой ожидаемое значение. Так как исходами являются доходности, ожидаемое значение — это ожидаемая доходность (expected rate of return, k), которую можно представить в следующем виде:

, где

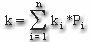
k_i — i-й возможный исход,
Р_i — вероятность появления i-го исхода,
n — число возможных исходов.

Используя формулу, находим, что ожидаемая доходность проекта 2 равна 12.0%

к = -2.0% * 0.05 + 9.0% * 0.20 + 12.0% * 0.50 + 15%* 0.20 + 26.0% * 0.05 = 12.0%

Ожидаемые доходности трех других альтернативных вариантов инвестирования найдены аналогичным образом (таблице 1).
Дискретные распределения вероятностей могут быть представлены графически или в табличной форме. На рисунке 1 приведены столбиковые диаграммы (или гистограммы) проектов №1 и №2.

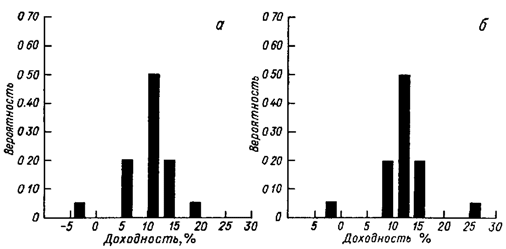
Рисунок 1. Графическое представление дискретного распределения вероятностей; а — проект №1; б — проект №2

Возможные значения доходности проекта №1 принадлежат промежутку от -3.0 до +19.0%, а проекта №2 от -2.0 до +26.0%. Отметим, что высота каждого столбца представляет собой вероятность появления соответствующего исхода, а сумма этих вероятностей по каждому варианту равна 1.00. Отметим также, что распределение значений доходности проекта №2 симметрично, тогда как соответствующее распределение для проекта №1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначейских векселей представлена единственным столбцом, а доходность корпорационных облигаций представлена диаграммой, имеющей правостороннюю асимметрию.

Программная реализация данной методики финансовой математики сделана в: «Альтаир Финансовый калькулятор 2.xx».

На примере расчета ожидаемой доходности можно увидеть, как применять программу «Альтаир Финансовый калькулятор 2.xx» на практике.

Главная Методики финансового и инвестиционного анализа Финансовая математика Производительность труда
Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.

Источник

CFA — Как оценивать вероятность событий при принятии финансовых решений?

Рассмотрим основные вероятностные инструменты, необходимые финансовому аналитику для прогнозирования и решения многих реальных проблем, связанных с риском, — в рамках изучения количественных методов по программе CFA.

Все инвестиционные решения принимаются в условиях риска. Инструменты, которые позволяют нам принимать решения последовательно и логично в этой ситуации, относятся к категории вероятностных. В этом чтении представлены основные вероятностные инструменты, необходимые для решения многих реальных проблем, связанных с риском.

Мы покажем, как эти инструменты применяются к решению таких вопросов, как прогнозирование эффективности работы инвестиционного управляющего, прогнозирование финансовых показателей и ценообразование облигаций таким образом, чтобы они справедливо компенсировали своим держателям риск дефолта.

При этом мы сфокусируемся на практических аспектах: подробно исследуем концепции, которые наиболее важны для инвестиционных исследований и практики.

Одной из таких концепций является независимость событий, поскольку она связана с предсказуемостью доходов и финансовых показателей. Другая — ожидание, так как аналитики постоянно смотрят в будущее в своих анализах и решениях.

Аналитики и инвесторы также должны справляться с изменчивостью. Здесь мы рассмотрим дисперсию или изменчивость ожиданий как концепцию риска, важную для инвестиций.

В этом разделе рассматриваются:

• Основные инструменты вероятности, в том числе математическое ожидание и дисперсия.
• Ковариация и корреляция (показатели взаимосвязи между случайными величинами) и принципы расчета ожидаемой доходности и дисперсии портфеля.
• Формула Байеса и подсчет результатов.

Формула Байеса — это процедура обновления (корректировки) убеждений на основе новой информации. В нескольких областях, включая широко используемую биномиальную модель ценообразования опционов, расчет вероятностей включает в себя определение и подсчет результатов.

Что такое вероятность события?

Вероятностные концепции и инструменты, необходимые для большей части работы финансового аналитика, относительно немногочисленны и просты, но требуют обдуманного применения.

В этом разделе представлены основы работы с вероятностью, ожиданиемым значением и дисперсией, — на примерах анализа рынка капитала и инструментов с фиксированным доходом.

Внимание инвестора сфокусировано на доходности. Доходность рискованного актива является примером случайной величины (англ. ‘random variable’), то есть величины, результаты (возможные значения) которой являются неопределенными.

Например, портфель может иметь целевую доходность 10% годовых. На данный момент портфельный менеджер может сосредоточиться на вероятности получения прибыли, которая в следующем году составит менее 10%.

10 процентов — это конкретное значение или результат случайной величины «доходность портфеля». Хотя мы можем быть обеспокоены одним результатом, часто наш интерес может быть связан с рядом результатов: понятие «событие» охватывает оба варианта.

Определение события.

Событие (англ. ‘event’) — это определенный набор результатов или исходов (англ. ‘outcomes’).

Мы можем определить событие как единый результат — например, портфель приносит доход 10% (курсивом выделено определение события).

Мы также можем отразить озабоченность менеджера портфеля, определив событие следующим образом: портфель приносит доход ниже 10%.

Это второе событие, относящееся ко всем возможным доходам, которые ≥ -100% (наихудший возможный доход), но

Насколько вероятно, что портфель получит доход ниже 10%?

Ответ на этот вопрос — вероятность (англ. ‘probability’): число от 0 до 1, которое измеряет вероятность того, что указанное событие произойдет. Если вероятность того, что портфель принесет доход ниже 10% составляет 0.40, это означает, что вероятность этого события составляет 40%.

• Если событие невозможно, оно имеет вероятность 0.
• Если событие обязательно произойдет, оно имеет вероятность 1.
• Если событие невозможно или произойдет в любом случае, оно вовсе не случайно.
• Диапазон от 0 до 1 включает все возможные значения вероятности.

Вероятность имеет два свойства, которые вместе составляют ее определение.

Определение вероятности.

Два определяющих свойства вероятности таковы:

1. Вероятность любого события E представляет собой число от 0 до 1: 0 ≤ P(E) ≤ 1.
2. Сумма вероятностей любого набора взаимоисключающих и исчерпывающих событий равна 1.

P с последующими круглыми скобками означает «вероятность (событие в скобках)», то есть P(E) — это «вероятность события E». Мы также можем думать о P как о правиле или функции, которая присваивает числовые значения событиям, соответствующим указанным выше свойствам 1 и 2.

В приведенном выше определении термин взаимоисключающий (англ. ‘mutually exclusive’) означает, что одновременно может происходить только одно событие; термин исчерпывающий (англ. ‘exhaustive’) означает, что события охватывают все возможные результаты.

События A = портфель с доходностью 10% и B = портфель с доходностью ниже 10% являются взаимоисключающими, поскольку A и B не могут происходить одновременно.

Например, доходность 8.1% означает, что событие B произошло, а событие A не произошло. Хотя события A и B являются взаимоисключающими, они не являются исчерпывающими, поскольку они не охватывают такие результаты, как доходность в 11%.

Предположим, мы определили третье событие: C = портфель приносит доход выше 10%.

Очевидно, что A, B и C являются взаимоисключающими и исчерпывающими событиями. Каждое из событий P(A), P(B) и P(C) является числом от 0 до 1, и
P(A) + P(B) + P(C) = 1.

Самым основным видом взаимоисключающих и исчерпывающих событий является набор всех различных возможных результатов случайной величины. Если мы знаем и этот набор, и распределение вероятностей для этих результатов (распределение вероятностей случайной величины) — у нас есть полное описание случайной величины, и мы можем назначить вероятность любому событию, которое мы можем описать.

В чтении об общих распределениях вероятностей мы опишем некоторые из распределений вероятностей, наиболее часто используемых в инвестиционной практике.

Вероятность любого события — это сумма вероятностей различных результатов, включенных в определение события.

Предположим, что интересующим событием является D = портфель приносит доход выше безрисковой ставки, и мы знаем распределение вероятностей доходности портфеля.

Предположим, безрисковая ставка составляет 4%. Чтобы вычислить P(D), т.е. вероятность события D, мы суммируем вероятности результатов, которые удовлетворяют определению события; то есть мы суммируем вероятности доходности портфеля более 4%.

Ранее, чтобы проиллюстрировать концепцию, мы предполагали вероятность 0.40 для портфеля с доходностью менее 10%, без обоснования конкретного предположения. Мы также говорили об использовании распределения вероятностей результатов для вычисления вероятности событий, не объясняя, как можно получить распределение вероятностей.

Принятие фактических финансовых решений с использованием неточных вероятностей может иметь серьезные последствия.

Как на практике мы оцениваем вероятность события?

Эта тема сама по себе является предметом изучения, но существует 3 основных подхода к оценке вероятностей.

1. В инвестициях мы часто оцениваем вероятность события как относительную частоту его возникновения, основываясь на исторических данных. Этот метод позволяет найти эмпирическую вероятность (англ. ’empirical probability’).

Например, Thanatawee (2013) сообщает, что в его выборке из 1927 ежегодных наблюдений за нефинансовыми фирмами SET (Фондовая биржа Таиланда) в период с 2002 по 2010 год 1382 были фирмами, выплачивающими дивиденды, и 545 были компаниями, не выплачивающими дивиденды. Таким образом, эмпирическая вероятность того, что тайская фирма выплатит дивиденды, составляет приблизительно 1 382/1 927 = 0,72.

2. Результаты должны стабильно прослеживаться с течением времени, чтобы эмпирические вероятности были точными. Мы не можем рассчитать эмпирическую вероятность события, отсутствующего в исторической записи, или достоверную эмпирическую вероятность очень редкого события.

Таким образом, существуют случаи, когда мы можем скорректировать эмпирическую вероятность, чтобы учесть восприятие меняющихся результатов.

3. В других случаях у нас вообще нет возможности использовать эмпирическую вероятность. Поэтому мы также можем сделать личную оценку вероятности без ссылки на какие-либо конкретные данные.

Каждый из этих трех типов вероятности является субъективной вероятностью (англ. ‘subjective probability’), основанной на личном или субъективном суждении.

Субъективные вероятности имеют большое значение в инвестициях. Инвесторы, принимая решения о покупке и продаже, которые определяют цены активов, часто опираются на субъективные вероятности.

Субъективные вероятности появляются в разных местах в этом чтении, особенно в обсуждении формулы Байеса.

В более узком диапазоне четко определенных проблем мы иногда можем вывести вероятности, рассуждая о проблеме. Результирующая вероятность — это априорная вероятность (англ. ‘a priori probability’), основанная на логическом анализе, а не на наблюдении или личном суждении.

Мы будем использовать этот тип вероятности в приведенном далее, в Примере (6).

Методы подсчета, которые мы обсудим позже, особенно важны при вычислении априорной вероятности.

Поскольку априорные и эмпирические вероятности обычно не зависят от конкретного человека, они часто группируются как объективные вероятности.

Источник