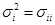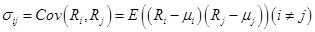Вектор ожидаемых доходностей активов

Управление портфелем краткосрочных государственных ценных бумаг

E(R) — вектор ожидаемых доходностей ценных бумаг, т.е. =Е(Ri)>0 (i=1, 2, ., N) — ожидаемая доходность ценной бумаги i за один период владения;

=E((R-)(R—)T) (i, j=1, 2, ., N) — ковариационная матрица доходностей ценных бумаг размерности (NxN). Матрица является симметричной, т.е. . Будем также предполагать, что она является невырожденной: . Диагональные элементы матрицы представляют собой дисперсии доходностей активов:

=D(Ri)=

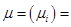
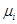
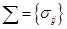
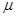
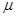
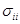
Для удобства будем также использовать обозначение

Среднеквадратическое отклонение 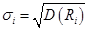> О доходности ценной бумаги i будем интерпретировать как риск ценной бумаги.

Недиагональные элементы матрицы являются коварициями доходностей ценных бумаг и определяются по формуле

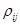
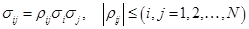
и связаны с коэффициентами корреляции доходностей соотношением:

. (28)

С учетом принятых обозначений и соглашений характеристики портфеля ценных бумаг для одного периода владения будут определяться следующими выражениями:

; (29)

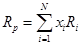
• ожидаемая доходность портфеля:

(30)

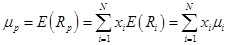
• дисперсия доходности портфеля:

(31)

(32)

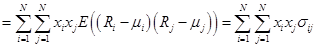
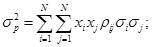
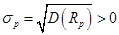
В аналитических исследованиях более удобной является векторно-матричная форма представления характеристик портфеля:

(33)

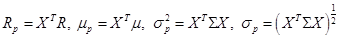
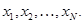
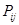
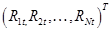
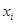
Пусть инвестор распределяет свой капитал среди N (N>1) рисковых активов в некоторых пропорциях Как известно, в рамках подхода «доходность — риск», предполагается, что цены <>, а следовательно, и доходности активов () являются случайными величинами. Из доходностей N активов за один и тот же период t образуем вектор доходностей Rt = а из величин <> — вектор, определяющий структуру портфеля X=(xh x2, .,xN)T.

Решение задачи формирования оптимального в смысле подхода «доходность — риск» портфеля основано на определенных модельных предположениях относительно:

• вероятностной модели доходностей (курсов) активов

• рынка и поведения его участников.

1) Предположения относительно вероятностной модели доходностей.

Уже обсуждались традиционные предположения относительно вероятностной модели доходностей в задаче оптимального портфельного инвестирования. Так же отмечались недостатки этих предположений с точки зрения адекватности соответствующей им модели.

В соответствии с этими предположениями, значения векторов доходностей , полученные за анализируемый исторический период, можно рассматривать как случайную выборку из многомерного нормального распределения, параметрами которого являются математическое ожидание вектора доходностей активов (т.е. вектор ожидаемых доходностей) , и ковариационная матрица вектора доходностей активов . Это позволяет не учитывать автокорреляцию значений доходностей и считать ожидаемые доходности активов, дисперсии и ковариации (ковариационную матрицу) доходностей активов постоянными во времени, т.е. полагать, что

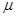
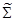
В качестве статистических оценок параметров и при этом теоретически могут использоваться выборочное среднее значение и выборочная ковариационная матрица . На практике, однако, как это будет показано, для оценивания неизвестных параметров приходится использовать различные «факторные» модели.

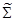
Найденные оценки , рассматриваются как прогнозные значения соответствующих характеристик в будущем периоде владения и используются вместо неизвестных истинных значений параметров в алгоритмах оптимизации структуры портфеля ценных бумаг для одного будущего периода владения, т.е. решаются однопериодные задачи оптимизации структуры портфеля активов для каждого периода владения независимо от других периодов.

2) Предположения относительно рынка и поведения его участников.

Данные предположения состоят в следующем:

М.1. Инвесторы осуществляют оценку портфелей, основываясь на ожидаемой доходности и риске активов.

М.2. При выборе их двух идентичных во всем, кроме ожидаемой доходности, портфелей инвестор отдает предпочтение портфелю с большей ожидаемой доходностью.

М.3. При выборе из двух идентичных во всем, кроме риска, портфелей инвестор отдает предпочтение портфелю с меньшим риском.

М.4. Характеристики активов и портфелей относятся к одному заданному периоду владения.

М.5. Активы являются бесконечно делимыми, т.е. в каждый актив может быть вложена любая доля капитала инвестора.

Источник

Экзамен 18 Январь 2016, вопросы и ответы

Образцы решения экзаменационных задач I.

Задачи на расчет сделок с комиссией.

Задача 1. Инвестор открыл портфельную сделку, купив 100 акций A по $100,00 и продав 40 акций В по $40,00. Спустя полгода он закрыл сделку по ценам $120,00 и $30,00 соответственно. За полгода по акциям А и В были получены дивиденды $10 и $5. Налог взимается с сальдо полного дохода сделки по ставке τ=15,00%. Годовой темп инфляции равен 10,00%, а ставка комиссии составляет α=2,00%. Решение. Согласно условию позиции портфеля по активам: zA = 100, zB = -40; начальные цены: P 0 A =$100,00 P 0 B =$40,00; а конечные P 1 A =$120,00 P 1 B =$30,00; Тогда начальные стоимости позиций: S 0 A = zA ∙P 0 A =100∙ $100,00 = $10 000,00; S 0 В = zВ∙P 0 В = -40∙ $40,00 = — $1600,00; начальная стоимость портфеля S 0 = S 0 A + S 0 B = $10 000,00 — $1600,00 = $8400,00. Соответственно конечные стоимости позиций: S 1 A = zA ∙P 1 A =100∙ $120,00 = $12 000,00; S 1 В = zВ∙P 1 В = -40∙ $30,00 = — $1200,00; конечная стоимость портфеля S 1 = S 1 A + S 1 B = $12 000,00 — $1200,00 = $10800,00. Ценовой доход портфеля равен I(p) = S = S 1 — S 0 = $10800,00 — $8400,00 = $2400, а текущий I(с) = zA ∙ IA(с) + zB ∙ IB(с) = 100∙$10,00 — 40∙$5,00 = $800, Начальный оборот сделки равен S 0  = S 0 A +  S 0 B = $10 000,00 + $1600,00 = $16 000,00. Начальная комиссия С 0 = αS 0  = 0,02∙ $16 000,00 = $320, Конечный оборот сделки равен S 1  = S 1 A +  S 1 B = $12 000,00 + $1200,00 = $13 200,00. Конечная комиссия С 1 = αS 1  = 0,02∙ $13 200,00 = $264, Полная комиссия С = С 0 + С 1 = $320,00 + $264,00 = $584, Ценовой доход с учетом комиссии равен Iα(p) = I(p) – С = $2400,00-$584,00 = $1816, Полный доход с учетом комиссии TIα = Iα(p) + I(с) = $1816,00 + $800,00 = $2616,00. Налог на полную прибыль Tax = TIα∙ τ = $2616,00∙0,15 = $392,40. Чистая прибыль NTI = $2616,00 — $392,40 = $2223,60. Начальный капитал сделки W 0 = S 0 + C 0 = $8400,00 + $320,00 = $8720, Доходность портфеля за период (полгода) r1/2 = NTI/W 0 = 0,255 или 25,5%. Эффективная годовая доходность yэф = (1+r1/2 )(1/0,5)-1 =(1+0,255) 2 -1= 0,5750 или 57,50% годовых. Реальная чистая годовая доходность равна (согласно ф-ле Фишера)

1 1 0,

  или 43,18% годовых.

Задача 2. Инвестор с капиталом в 100 000$ сформировал портфель из акций A и B с вектором весов w = (1,5; -0,5) Начальные цены акций $100,00 и $40,00 соответственно. Найти вектор позиций сделки с учетом комиссии равной 2,00%.

Решение. Обозначим через S 0 начальную стоимость портфеля. Тогда суммы средств вложенных в активы А и В будут равны S 0 A = wA ∙S 0 =1,5∙ S 0 ; S 0 B = wB ∙S 0 = -0,5∙ S 0 ; Начальный оборот портфеля равен S 0  = S 0 A +  S 0 B =wA ∙S 0  +  wB ∙S 0  = S 0 (wA +  wB ) =2S 0 Тогда начальная комиссия С 0 = αS 0  = 0,02∙2S 0 = 0,04S 0. Начальный капитал W 0 = S 0 + C 0 = S 0 + 0,04S 0 = 1,04S 0 = $100 000. Следовательно S 0 =$100 000/1,04 = $96153,85. Тогда S 0 A = wA ∙S 0 =1,5∙ $96153,85= $144230,77 и S 0 В= wВ ∙S 0 = -0,5∙ $96153,85= -$48076,92. Учитывая начальные цены акций, получим позиции по ним в портфеле:

zA = S 0 A/P 0 A = $144230,77/$100,00 = 1442, zВ = S 0 В/P 0 В = -$48076,92/$40,00 = -1201,92.

Задача 3. Инвестор с начальным капиталом 100000 долл. Формирует портфель из активов А 1 и A 2 по начальной цене $100 и $50 соответственно. Конечная цена активов А 1 и A 2 равна $120 и $ соответственно. Найти максимальную прибыль за полгода, которую может заработать инвестор с учетом комиссии 2,00% (но без налогов) если веса активов удовлетворяют ограничениям: a 1 = -1 a 2 = -0, b 1 = 3 b 2 = 5, Решение. Обозначим через S 0 начальную стоимость портфеля. Пусть веса портфеля с наибольшей прибылью равны w 1 и w 2. Тогда как в предыдущей задаче получим W 0 = S 0 + C 0 = S 0 + αS 0  = S 0 [1+ α(w 1  +  w 2 )] Откуда S 0 = W 0 /[1+ α(w 1  +  w 2 )] Поскольку -1≤w 1 ≤3 и -0,5≤w 2 ≤5, То подставляя w 2 =1-w 1 в второе неравенство получим -0,5≤ 1-w 1 ≤5, или -4,5≤ w 1 ≤1, Совместно с первым неравенство это дает ограничение на вес первого (более доходного) актива -1≤ w 1 ≤1,5. Доходности активов равны соответственно r 1 =$120/$100-1=0,2 и r 2 =$40/$50-1= -0, Тогда доходность портфеля без учета комиссии равна rπ = r 1 w 1 + r 2 w 2 = r 1 w 1 + r 2 (1-w 1 ) = r 2 + w 1 (r 1 -r 2 ) = -0,2 +0,4w 1. Без учета комиссии веса портфеля с наибольшей прибылью будут w 1 =1,5 и w 2 = -0, а максимальная доходность портфеля составит rπ = -0,2 +0,4∙1,5 = 0,4. Начальная стоимость такого портфеля будет равна S 0 = W 0 /[1+ α(wA +  wB )]=$100 000/1,04 = $96153,85. Тогда S 01 = w 1 ∙S 0 =1,5∙ $96153,85= $144230,77 и S 02 = 2 ∙S 0 = -0,5∙ $96153,85= -$48076,92. Начальный оборот портфеля S 0  = S 01  +  S 02  = $144230,77 + $48076,92. = $192307,69. Начальная комиссия С 0 = αS 0  = 0,02∙ $192307,69 = $3846, Конечные стоимости позиций будут равны S 11 = S 01 (1+ r 1 ) = $144230,77∙1,2 = $173076, S 12 = S 02 (1+ r 2 ) = -$48076,92∙0,8= — $38461,54.

Задача 4. Пусть на рынке из акций А 1 , А 2 и А 3 допустимо формирование портфелей w=(w 1 ,w 2 ,w 3 ) веса которых удовлетворяют ограничениям ai ≤ wi ≤ biгде a 1 = 0,1 a 2 = -0,5 a 3 = -0,1 0 b 1 = 3 b 2 =2,0 b 3 = 4 8, Начальные цены акций А 1 , А 2 и А 3 равны $100,00; $50,00; $80,00 а конечные — $120,00; $55,00; $60,00 соответственно. Какую максимальную прибыль (без учета комиссии и налогов) может получить инвестор с начальным капиталом 10000$, если он формирует допустимый портфель из акций А 1 , А 2 и А 3. Дивиденды не учитывать. Решение. Найдем сначала доходности активов

r 1 =$120/$100-1= 0,2; r 2 =$55/$50-1= 0,1 и r 3 =$40/$80-1 = -0, Тогда доходность портфеля без учета комиссии равна rπ = r 1 w 1 + r 2 w 2 + r 3 w 3 = 0,2w 1 + 0,1w 2 -0,5w 3 ; w 1 + w 2 + w 3 =1. Поскольку доходность линейная функция весов (при заданных доходностях активов) то максимальное значение возможно только на граничных значениях этих весов. Это означает что начав с любого допустимого портфеля нужно максимальным образом увеличивать веса более доходных и на ту же величину (чтобы сохранить портфельное ограничение – сумму весов равной

1) уменьшать веса менее доходных активов. Возьмем в качестве исходного портфель w 1 = 0,1; w 2 = -0,1; w 3 =1. Это, очевидно, допустимый портфель. Его доходность rπ = 0,2∙0,1 — 0,1∙0,1 -0,5∙1= -0, Будем увеличивать вес w 1 (наиболее доходного актива) А 1 и одновременно уменьшать на эту же величину вес w 3 (самого низкодоходного) актива А 3. Предельное возможное увеличение w 1 (с 0, до 3) составляет 3-0,1= 2,9 а предельное возможное уменьшение w 3 (с 1 до -0,1) составляет 1-(-0,1)=1,1. Это значит, что одновременно можно увеличить w 1 на 1,1 с 0,1 до 1,2, и уменьшить w 3 с 1 до предельного значения -0,1. Поэтому получился новый портфель w 1 =1,2; w 2 = -0,1; w 3 = -0, с доходностью rπ = 0,2∙1,2 — 0,1∙0,1 +0,5∙0,1 = 0,28. Поскольку уменьшать вес w 3 более невозможно, будем увеличивать вес w 1 актива А 1 (более доходного чем А 2 ) и одновременно уменьшать вес w 2 менее доходного актива А 1. Предельное увеличение w 1 (с 1,2 до 2) составляет 2-1,2=0,8 а предельное уменьшение веса w 2 (с -0,1 до -0,5) составляет -0,1- (-0,5) = 0,4. Поэтому одновременно возможно только увеличить вес w 1 на 0, с 1,2 до 1,6 и уменьшить w 2 на 0,4 с -0,1 до -0,5 предельного значения -0,5. В итоге получим портфель w 1 =1,6; w 2 = -0,5; w 3 = -0, с доходностью rπ = 0,2∙1,6 — 0,1∙0,5 +0,5∙0,1 = 0,32. Полученный портфель имеет максимальную доходность 0,32 или 32%. Поэтому наибольшая возможная прибыль составляет Imax = $10000∙0.32= $3200.

Образцы решения экзаменационных задач II.

Двумерные задачи оптимизации портфелей в моделях Блека и Марковица

Задача 1. Заданы следующие параметры рынка из двух активов А 1 , А 2.

Источник