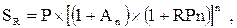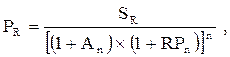Уровень доходности с учетом фактора риска

Формирование необходимого уровня доходности финансовых операций с учетом фактора риска

III Аналоговые методы оценки уровня финансового риска

II Экспертные методы оценки уровня финансового риска

Экспертные методы оценки уровня финансового риска применяют в том случае, если на предприятии отсутствуют необходимые данные для выполнения расчетов экономико-статистическими методами. Эти методы базируются на опросе квалифицированных специалистов с последующей математической обработкой результатов этого опроса.

В процессе экспертной оценки каждому эксперту предлагается оценить уровень возможного риска, основываясь на определенной балльной шкале, например:

— риск отсутствует: 0 баллов;

— риск незначительный: 10 баллов;

— риск ниже среднего: 30 баллов;

— риск среднего уровня: 50 баллов;

— риск выше среднего уровня: 70 баллов;

— риск высокий: 90 баллов;

— риск очень высокий 100 баллов.

Аналоговые методы позволяют определить уровень рисков по отдельным наиболее массовым финансовым операциям предприятия. При этом может быть использован как собственный, так и внешний опыт осуществления таких финансовых операций.

В процессе управления финансовой деятельностью необходимо обеспечивать количественную пропорциональность доходности и риска.

1. При определении необходимого уровня премии за риск используется формула:

RP_n – уровень премии за риск по конкретному финансовому (фондовому) инструменту;

R_n — средняя норма доходности на финансовом рынке;

А_n — безрисковая норма доходности на финансовом рынке;

b — бета-коэффициент, характеризующий уровень систематического риска по конкретному (фондовому) инструменту.

Необходимо расcчитать уровень премии за риск по трем видам акций.

Варианты акций	Средняя норма доходности на фондовом рынке, %	Безрисковая норма доходности ,%	Бета-коэффициент по акциям	Уровень премии за риск (определенный по формуле), %
Акция 1 Акция 2 Акция 3	12,0 12,0 12,0	5,0 5,0 5,0	0,8 1,0 1,2	5,6 7,0 8,4

Уровень премии за риск возрастает пропорционально росту бета-коэффициента, т. е. уровня систематического риска.

2. Сумма премии за риск рассчитывается по формуле:

RP_s — сумма премии за риск по конкретному финансовому (фондовому) инструменту в настоящей стоимости;

SI – стоимость (котируемая цена) конкретного финансового (фондового) инструмента;

RP_n – уровень премии за риск по конкретному финансовому инструменту, выраженный десятичной дробью.

Исходя из конкретной цены трех акций на фондовом рынке и уровня премии за риск по ним, определить сумму премии по каждой акции.

Таблица — Расчет необходимой суммы премии за риск

Варианты акций	Котируемая цена акций на фондовом рынке	Уровень премии за риск	Сумма премии за риск
Акция 1 Акция 2 Акция 3	0,056 0,070 0,084	5,6 4,9 7,6

3. Общий уровень доходности финансовых операций с учетом фактора риска рассчитывается по формуле:

Таблица — Расчет необходимого общего уровня доходности

Источник

По трем акциям

Варианты акций	Везрисковая норма доходности на фондовом рынке, %	Уровень премии за риск, %	Необходимый общий уровень доходности (определенный по формуле), %
Акция 1 Акция 2 Акция 3	5,0 5,0 5,0	5,6 7,0 8,4	10,6 12,0 13,4

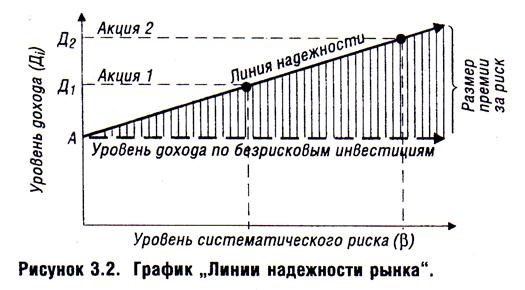
Изложенный выше методический инструментарий формирова­ния необходимого уровня доходности финансовых операций с учетом фактора риска построен на „Ценовой Модели Капитальных Активов», разработанной Г. Марковичем и У. Шарпом (за разработку этой Мо­дели они были удостоены в 1990 году Нобелевской премии). Графи­ческую интерпретацию этой Модели составляет график „Линии на­дежности рынка» (рис. З.2.).

Отдельные точки на „Линии надежности рынка» показывают не­обходимый уровень доходности по ценной бумаге (с учетом премии

за риск) в зависимости от уровня систематического риска по ней, измеряемого бета-коэффициентом.

III. Методический инструментарий оценки стоимости денеж­ных средств с учетом фактора рискадает возможность осущест­влять расчеты как будущей, так и настоящей их стоимости с обеспе­чением необходимого уровня премии за риск.

1. При оценке будущей стоимости денежных средств с уче­том фактора риска используется следующая формула:

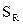
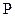
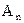
где — будущая стоимость вклада (денежных средств), учиты­вающая фактор риска;

— первоначальная сумма вклада;

— безрисковая норма доходности на финансовом рынке,

выраженная десятичной дробью;

— уровень премии за риск по конкретному финансовому инструменту (финансовой операции), выраженный деся­тичной дробью;

— количество интервалов, по которым осуществляется каж­дый конкретный платеж, в общем обусловленном перио­де времени.

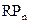
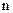
Пример: Необходимо определить будущую стоимость вклада с учетом фактора риска при следующих условиях: первоначальная сумма вклада составляет 1000 усл. ден. ед.; безрисковая норма доходности на финансовом рынке состав­ляет 5%;

уровень премии за риск определен В размере 7%; общий период размещения вклада составляет 3 года при начислении процента один раз в год.

Подставляя эти показатели в вышеприведенную фор-мулу, получим: будущая стоимость вклада, учитывающая фактор риска =

усл. ден. ед.

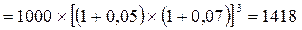
2. При оценке настоящей стоимости денежных средств с учетом фактора риска используется следующая формула:

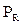
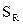
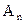
где – настоящая стоимость вклада (денежных средств), учитывающая фактор риска;

— ожидаемая будущая стоимость вклада (денежных средств);

— безрисковая норма доходности на финансовом рынке,

выраженная десятичной дробью;

— уровень премии за риск по конкретному финансовому инструменту (финансовой операции), выраженный деся­тичной дробью;

— количество интервалов, по которым осуществляется каж­дый конкретный платеж, в общем обусловленном перио­де времени.

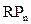
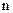
Пример: Необходимо определить настоящую сто­имость денежных средств с учетом фактора риска при сле­дующих условиях:

ожидаемая будущая стоимость денежных средств — 1000 усл. ден. ед.;

безрисковая норма доходности на финансовом рынке состав­ляет 5%;

уровень премии за риск определен в размере 7%; период дисконтирования составляет 3 года, а его интер­вал — 1 год.

Подставляя эти данные в вышеприведенную формулу, получим: настоящая стоимость денежных средств с учетом фактора

риска 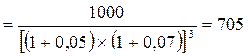усл. ден. ед.

Проведенный обзор показывает, что методический инструмен­тарий учета фактора риска в управлении финансовой деятельностью предприятия является довольно обширным и позволяет решать мно­гообразные задачи в этой сфере финансового менеджмента. Более глубокое изложение вопросов управления финансовыми рисками рас­сматривается в специальном разделе.

Источник

Соотношение риска и доходности инвестиций

В процессе формирования своего портфеля ценных бумаг каждый инвестор неизбежно сталкивается с таким понятием как соотношение риска и доходности (как для отдельно взятого финансового инструмента входящего в его портфель, так и для всего портфеля в целом). Существует целая портфельная теория, разработанная американским экономистом Гарри Марковицем, направленная на то чтобы включать в свой портфель только те финансовые инструменты, для которых соотношение риска к доходности является оптимальным.

Или, другими словами, теория эффективного портфеля Марковица даёт ответ на вопрос о том, какой уровень доходности является приемлемым (оптимальным) для того уровня риска, который готов взять на себя инвестор.

Давайте, для начала определимся с основными терминами.

Риском называется вероятность того, что инвестиция в определённый финансовый инструмент (или в группу финансовых инструментов – инвестиционный портфель) не только не принесёт желаемого уровня прибыли, но и повлечёт за собой убыток. Уровень риска удобно выражать в процентах от суммы инвестируемого капитала. Так, например, величина риска в 100% говорит о полной потере инвестируемого капитала, а риск в 50% – о потере его половины.

Доходностью называют ту прибыль, которую приносит финансовый инструмент, выбранный в качестве объекта для инвестиций (или весь портфель целиком). Её также обычно выражают в процентах от инвестируемого капитала.

Для того чтобы понять какое соотношение риска и доходности является оптимальным, давайте рассмотрим вот этот график:

Кривая риск/доходность в теории Гарри Марковица

График построен на основе решения задачи по оптимизации инвестиционного портфеля (квадратической оптимизации при линейных ограничениях). Формулировка этой задачи выглядит примерно следующим образом:

Не вникая далее в премудрости высшей математики, давайте проанализируем вышеозначенный график с точки зрения простого инвестора.

Как видите, на нём есть линия красного цвета, обозначенная как граница эффективности. Эта именно та линия, на которой находятся оптимальные значения соотношения риска к доходности анализируемого финансового инструмента. Нижняя её часть соответствует небольшой доходности при таком же относительно небольшом уровне риска, средняя часть – среднему уровню доходности при среднем же риске, верхняя часть – высокому уровню доходности при большом уровне риска.

Нижняя часть границы эффективности содержит значения соотношения риска к доходности, удовлетворяющие консервативных инвесторов, а в верхней её части находятся значения, которые устраивают инвесторов с агрессивными стратегиями инвестирования.

Теперь давайте обратим своё внимание на области находящиеся выше и ниже границы эффективности. Всё множество значений находящееся ниже границы эффективности, представляет собой неоптимальное соотношение риска к доходности, то есть риск здесь относительно велик при сравнительно небольшом уровне доходности.

Вы же не станете инвестировать в акции с доходностью ниже или равной проценту по банковскому депозиту? Ведь акции (даже принадлежащие к категории голубых фишек), это относительно рискованный финансовый инструмент, который может принести как прибыль, так и убыток. А банковский депозит, с учётом того, что вклады физических лиц подлежат программе обязательного страхования, с вероятностью близкой к ста процентам, принесёт пусть небольшую, но всё же прибыль.

На вышеозначенном графике, точка соответствующая инвестициям в банковские депозиты находится на границе эффективности (в нижней её части), а точка соответствующая инвестициям в акции с такой же доходностью, расположена на том же уровне, но значительно правее границы эффективности.

А вот ту область, которая находится выше границы эффективности, можно отнести к миру заоблачных фантазий, поскольку в реальности такие соотношения риска к доходности попросту невозможны. Когда, например, кто-либо предлагает вам инвестировать свои деньги под высочайший процент и с небольшим уровнем риска, то он предлагает невозможное, то есть, по сути, он вас обманывает.

В общем и целом из всего вышесказанного можно извлечь следующие основные выводы:

1. Величина потенциальной доходности финансового инструмента неизбежно зависит от величины связанного с ним риска. Или, иными словами, чем больше доходность, тем больше риск и наоборот;
2. Невозможно получить высокий уровень дохода, не подвергаясь при этом повышенному риску;
3. Портфель инвестора следует составлять из бумаг соотношение риска и доходности которых, соответствует значениям лежащих на границе эффективности.

Источник