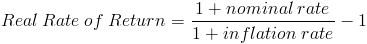Геометрическая разница, считаем реальную доходность
В прошлой публикации Где интуиция не срабатывает: считаем доходность мы рассказывали об алгебраической и геометрической суммах. Речь шла о том, как правильно считать доходность.
Когда мы употребляем термин доходность, то в большинстве случаев имеется ввиду номинальная доходность, то есть без учета инфляции. Как правило, инвестора интересует реальная доходность с учетом влияния инфляции.
Как и в прошлой статье начнем с простого примера. Если доходность депозита составила 18% годовых, а инфляция за тот же период — 11%, какова итоговая доходность?
Проверьте себя. Как бы вы посчитали результат?
Что случится, если вдруг инфляция в этот год взлетит до 118%?
Довольно часто в первом случае люди полагают, что Реальная доходность составила 7%:
Такое вычитание называется алгебраическим.
Работает ли алгебраическое вычитание во втором случае?
Может ли реальная доходность достигать -100% после учета инфляции? Это значило бы, что покупательная сила денег стала равной нулю. А если инфляция составила бы 120%, мы потеряли бы больше денег, чем у нас было? Вряд ли такой метод вычитания может быть правильным …
Как и раньше, помогает геометрическая разница:
При расчете процентные соотношения переводятся в десятичные дроби, хотя в EXCEL можно этого не делать. EXCEL умеет сам переводить из дробей в проценты и наоборот (см. прилагаемый файл).
Обобщаем
Если доходность составила R процентов, а инфляция равняется N, то реальная доходность вычисляется по формуле:
Всегда ли неправильно считать доходность через алгебраическую сумму?
В примере, когда номинальная доходность составила 18% а инфляция – 11%, можно заметить, что результаты алгебраического и геометрического вычитания довольно близки. Ошибка составит лишь 0,69%.
Действительно, иногда полезно пользоваться алгебраической разницей для получения приближенных результатов. Ошибка будет незначительной в тех случаях, когда инфляция и доходность не слишком сильно отличаются.
Тем не менее, когда рассматриваются доходности за несколько периодов или когда разница между номинальной доходностью и инфляцией значительна, величина ошибки возрастает.
Источник
Как правильно считать реальную доходность с учетом инфляции?
Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018

Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.
Большинство инвесторов считают реальную доходность по простой формуле:
Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.
За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:
Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция
Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.
Еще одна формула, которая дает тот же результат, выглядит так:
Источник
Учет инфляции в бизнес-планировании и при проведении финансовых операций
В бизнес-планировании постоянно приходится считаться с фактором инфляции, которая с течением времени обесценивает стоимость находящихся в обращении денежных средств.
Влияние инфляции сказывается на многих аспектах финансовой деятельности предприятия. В процессе инфляции происходит относительное занижение стоимости отдельных материальных активов, используемых предприятием (основных средств, запасов товарно-материальных ценностей и т.п.); снижение реальной стоимости денежных и других финансовых его активов (дебиторской задолженности, нераспределенной прибыли, инструментов финансового инвестирования и т.п.); занижение себестоимости производства продукции, вызывающее искусственный рост суммы прибыли и приводящее к росту налоговых отчислений с нее; падение реального уровня предстоящих доходов предприятия и т.п. Особенно сильно фактор инфляции сказывается на проведении долгосрочных финансовых операций предприятия.
Концепция учета влияния фактора инфляции в бизнес-планировании заключается в необходимости реального отражения стоимости его активов и денежных потоков, а также в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами, при осуществлении различных финансовых операций.
Для оценки интенсивности инфляционных процессов в стране используются два основных показателя, учитывающих фактор инфляции в финансовых вычислениях — темп и индекс инфляции:
- Темп инфляции характеризует показатель, отражающий размер обесценения (снижения покупательной способности) денег в определенном периоде, выраженный приростом среднего уровня цен в процентах к их номиналу на начало периода.
- Индекс инфляции характеризует показатель, отражающий общий рост уровня цен в рассматриваемом периоде, определяемый путем суммирования базового их уровня на начало периода (принимаемого за единицу) и темпа инфляции в этом же периоде (выраженного десятичной дробью).
При расчетах, связанных с корректировкой стоимости денег с учетом фактора инфляции принято использовать два понятия — номинальная и реальная сумма денежных средств:
- Номинальная сумма денежных средств отражает оценку размеров денежных активов в соответствующих денежных единицах без учета изменения покупательной стоимости денег в рассматриваемом периоде.
- Реальная сумма денежных средств отражает оценку размеров денежных активов с учетом изменения уровня покупательной стоимости денег в рассматриваемом периоде, вызванного инфляцией.
Для расчета этих сумм денежных средств в процессе наращения или дисконтирования стоимости денег во времени используются соответственно номинальная и реальная ставка процента:
- Номинальная процентная ставка характеризует ставку процента, устанавливаемую без учета изменения покупательной способности денег в связи с инфляцией (или общую процентную ставку, в которой не элиминирована ее инфляционная составляющая).
- Реальная процентная ставка характеризует ставку процента, устанавливаемую с учетом изменения покупательной стоимости в рассматриваемом периоде в связи с инфляцией.
С учетом рассмотренных базовых понятий формируется конкретный методический инструментарий, позволяющий учесть фактор инфляции в процессе бизнес-планирования.
I. Инструментарий прогнозирования годового темпа и индекса инфляции основывается на ожидаемых среднемесячных ее темпах. Такая информация содержится в публикуемых прогнозах экономического и социального развития страны на предстоящий период. Результаты прогнозирования служат основой последующего учета фактора инфляции в финансовой деятельности предприятия.
1. При прогнозировании годового темпа инфляции используется следующая формула:
ТИГ = (1 + ТИМ)12 — 1 ,
где ТИГ — прогнозируемый годовой темп инфляции, выраженный десятичной дробью; ТИМ — ожидаемый среднемесячный темп инфляции в предстоящем периоде, выраженный десятичной дробью.
Пример 1. Необходимо определить годовой темп инфляции, если в соответствии с прогнозом экономического и социального развития страны (или собственными прогнозными расчетами) ожидаемый среднемесячный темп инфляции определен в размере 3%.
Подставляя это значение в формулу, получим: Прогнозируемый годовой темп инфляции составит:
(1 + 0,03)12 — 1 = 14258 -1 = 0,4258 или 42,58%.
По указанной формуле может быть рассчитан не только прогнозируемый годовой темп инфляции, но и значение этого показателя на конец любого месяца предстоящего года.
2. При прогнозировании годового индекса инфляции используются следующие формулы:
ИИГ = 1 + ТИГ или ИИГ = (1 + ТИМ)12 ,
где ИИГ — прогнозируемый годовой индекс инфляции, выраженный десятичной дробью; ТИГ — прогнозируемый годовой темп инфляции, выраженный десятичной дробью (рассчитанный по ранее приведенной формуле); ТИМ — ожидаемый среднемесячный темп инфляции, выраженный десятичной дробью.
Пример 2. Исходя из условий предыдущего примера, необходимо определить прогнозируемый годовой индекс инфляции.
Он равен: 1 + 0,4258 = 1,4258 (ими 142,6%), или (1 + 0,03)12 = 1,4258 (или 142,6%).
II. Инструментарий формирования реальной процентной ставки с учетом фактора инфляцииосновывается на прогнозируемом номинальном ее уровне на финансовом рынке (результаты такого прогноза отражены обычно в ценах фьючерсных и опционных контрактов, заключаемых на фондовой бирже) и результатах прогноза годовых темпов инфляции. В основе расчета реальной процентной ставки с учетом фактора инфляции лежит Модель Фишера, которая имеет следующий вид:
Ip = ( I — ТИ) / (1 + ТИ)
где Ip — реальная процентная ставка (фактическая или прогнозируемая в определенном периоде), выряженная десятичной дробью; I — номинальная процентная ставка (фактическая или прогнозируемая в определенном периоде), выраженная десятичной дробью; ТИ —темп инфляции (фактический или прогнозируемый в определенном периоде), выраженный десятичной дробью.
Пример 3. Необходимо рассчитать реальную годовую процентную ставку на предстоящий год с учетом следующих данных: номинальная годовая процентная ставка по опционным и фьючерсным операциям на фондовой бирже на предстоящий год сложилась в размере 19%; прогнозируемый годовой темп инфляции составляет 7%. Подставляя эти данные в Модель Фишера получим: реальная годовая процентная ставка прогнозируется в размере:
(0,19 — 0,07) / (1 + 0,07) = 0,112 (или 11,2%).
III. Инструментарий оценки стоимости денежных средств с учетом фактора инфляции позволяет осуществлять расчеты как будущей, так и настоящей их стоимости с соответствующей «инфляционной составляющей». В основе осуществления этих расчетов лежит формируемая реальная процентная ставка.
1. При оценке будущей стоимости денежных средств с учетом фактора инфляции используется следующая формула (представляющая собой модификацию рассмотренной ранее Модели Фишера):
Sн = P x [(1 + Iр) х (1 + ТИ) ]n
где Sн — номинальная будущая стоимость вклада (денежных средств), учитывающая фактор инфляции; Р— первоначальная сумма вклада; Iр — реальная процентная ставка, выраженная десятичной дробью; ТИ — прогнозируемый темп инфляции, выраженный десятичной дробью; n — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.
Пример 4. Определить номинальную будущую стоимость вклада с учетом фактора инфляции при следующих условиях: первоначальная сумма вклада составляет 1000 усл. ден. ед.; реальная годовая процентная ставка, используемая для наращения стоимости вклада, составляет 20%; прогнозируемый годовой темп инфляции составляет 12%; общий период размещения вклада составляет 3 года при начислении процента один раз в год.
Подставляя эти показатели в вышеприведенную формулу, получим:
Sн = 1000 x [(1 + 0,20) х (1 + 0,12)]3 = 2428 усл. ден. ед.
2. При оценке настоящей стоимости денежных средств с учетом фактора инфляции используется следующая формула:
Pр = Sн / [(1 + Iр) х (1 + ТИ) ]n
Пример 5. Необходимо определить реальную настоящую стоимость денежных средств при следующих условиях: ожидаемая номинальная будущая стоимость денежных средств составляет 1000 усл. ден. ед. реальная процентная ставка, используемая в процессе дисконтирования стоимости, составляет 20% в год; прогнозируемый годовой темп инфляции составляет 12%; период дисконтирования составляет 3 года, а его интервал — 1 год.
Подставляя эти показатели в вышеприведенную формулу, получим:
Pр = 1000 / [(1 + 0,20) х (1 + 0,12)]3 = 412 усл. ден. ед.
IV. Инструментарий формирования необходимого уровня доходности финансовых операций с учетом фактора инфляции, с одной стороны, призван обеспечить расчет суммы и уровня «инфляционной премии», а с другой — расчет общего уровня номинального дохода, обеспечивающего возмещение инфляционных потерь и получение необходимого уровня реальной прибыли.
1. При определении необходимого размера инфляционной премии используется следующая формула:
где Пи — сумма инфляционной премии в определенном периоде; Р — первоначальная стоимость денежных средств; ТИ — темп инфляции в рассматриваемом периоде, выраженный десятичной дробью.
2. При определении общей суммы необходимого дохода по финансовой операции с учетом фактора инфляции используется следующая формула:
где Дн — общая номинальная сумма необходимого дохода по финансовой операции с учетом фактора инфляции в рассматриваемом периоде; Др — реальная сумма необходимого дохода по финансовой операции в рассматриваемом периоде, исчисленная по простым или сложным процентам с использованием реальной процентной ставки; Пи — сумма инфляционной премии в рассматриваемом периоде.
3. При определении необходимого уровня доходности финансовых операций с учетом фактора инфляции используется следующая формула:
где УДн — необходимый уровень доходности финансовых операций с учетом фактора инфляции, выраженный десятичной дробью; Дн — общая номинальная сумма необходимого дохода по финансовой операции в рассматриваемом периоде; Др — реальная сумма необходимого дохода по финансовой операции в рассматриваемом периоде.
Следует отметить, что прогнозирование темпов инфляции представляет собой довольно сложный и трудоемкий вероятностный процесс, в значительной степени подверженный влиянию субъективных факторов. Поэтому в практике финансового менеджмента может быть использован более простой способ учета фактора инфляции.
В этих целях стоимость денежных средств при их последующем наращении или размер необходимого дохода при последующем его дисконтировании пересчитывается заранее из национальной валюты в одну из «сильных» (т.е. в наименьшей степени подверженных инфляции) свободно конвертируемых валют по курсу на момент проведения расчетов.
Процесс наращения или дисконтирования стоимости осуществляется затем по реальной процентной ставке (минимальной реальной норме прибыли на капитал). Такой способ оценки настоящей или будущей стоимости необходимого дохода позволяет вообще исключить из ее расчетов фактор инфляции внутри страны.
Источник