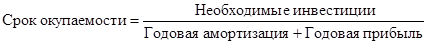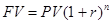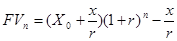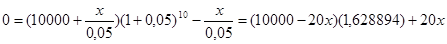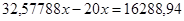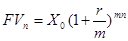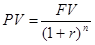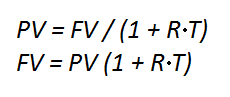Ценность денег во времени инвестиции

Инвестиции. Стоимость денег во времени.

Инвестициями называют все виды активов (средств), вкладываемых в хозяйственную деятельность в целях получения дохода — это их финансовое определение.

В экономической литературе различают инвестиции валовые и чистые.

Валовые инвестиции представляют собой общий объем производства капитальных товаров в течение определенного периода времени, обычно за год.

Чистые инвестиции — это ежегодное увеличение основного капитала. Они определяются так: Валовые инвестиции — Амортизация = Чистые инвестиции.

Для организации предпринимательского бизнеса на его начальной стадии приходится осуществлять первоначальное вложение капитала. Выделяют стартовый капитал, представляющий собой сумму первоначального капитала и текущих расходов на начальной стадии производства. Стартовый первоначальный капитал расходуется на регистрацию предприятия, открытие банковского счета, покупку здания или права на его аренду, ремонт или перестройку здания, покупку машин, оборудования, приборов, патентов, лицензий.

Текущие расходы включают покупку сырья и материалов, арендную плату, зарплату, отчисления в социальные фонды и пр.

Источники покрытия стартового капитала и пополнения средств предпринимателя могут быть как собственные (внутренние), так и заемные (внешние).

К собственным источникам относятся: прибыль от основной деятельности, прибыль от финансовых операций, другие виды доходов, уставный фонд, амортизационный фонд, задолженность покупателей за отгруженные товары, выручка от реализации выбывшего имущества, мобилизация внутренних ресурсов в строительстве и пр.

К заемным источникам относят: кредиты и ссуды, устойчивые пассивы и кредиторскую задолженность.

Первоначальное формирование финансовых ресурсов происходит в момент учреждения предприятия, когда образуется уставный капитал.

Уставный капитал — источник основных и оборотных средств фирмы, формируемый при ее организации. В качестве источников формирования уставного капитала могут выступать: акционерный капитал, паевые взносы учредителей, отраслевые финансовые ресурсы (при сохранении отраслевых структур), долгосрочный кредит, бюджетные средства. Величина уставного капитала показывает размер тех денежных средств (основных и оборотных), которые инвестированы в процесс производства.

Внешнее финансирование может осуществляться путем получения или путем выпуска акций. Акция — ценная бумага, свидетельствующая о внесении денежной суммы ее владельцем и дающая право на получение дивиденда, а также участие в управлении данной компанией.

Финансирование корпораций посредством выпуска новых акций — самый дорогостоящий способ финансирования.

Инвестиционная привлекательность фирмы может быть охарактеризована сроком окупаемости:

При инвестировании необходимо сопоставлять затраты и доходы (выгоды), возникающие в разное время. Затраты на осуществление проекта растягиваются во времени, а доходы возникают обычно после осуществления затрат. Поэтому говорят о таком понятии, как стоимость денег во времени. Оно Стоимость денег во времени — это принцип, согласно кото­рому до тех пор, пока существуют альтернативные возможности получения дохода, стоимость денег во времени зависит от того момента, когда ожидается их получение (то есть рубль, потраченный раньше, стоит больше, чем рубль, потраченный позже).

Общепринятой в финансовом анализе базовой формулой будущей стоимости является следующее выражение:

FV – будущая стоимость;

PV – текущая стоимость;

— коэффициент будущей стоимости.

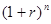
При расчете будущей стоимости определенной суммы денег используется техника сложного процента. Сложный процент — это начисление процентов на проценты. Проценты, вычисленные по истечении определенного периода (например, года), добавляются к основной сумме и включаются в ту сумму, на которую в следующий период будут начисляться проценты.

Для упрощения расчета будущей стоимости инвесторы и делающие сбережения лица могут использовать «правило 72-х», позволяющее определить период удвоения суммы денег при данной ставке процента с начислением процентов раз в год.

Для этого необходимо разделить 72 на ставку процента.

Например, инвестиции в сумме 10 млн. руб., приносящие доход 8% в год, удвоились бы через 9 лет (72 : 8).

Другой эмпирической закономерностью является «правило 7-10», согласно которому сумма удваивается через 10 лет при 7% годовых или через 7 лет при 10% годовых. Однако инфляция тоже развивается по принципу сложного процента. В условиях инфляции эти планируемые 20 млн. руб. через 9 лет будут стоить меньше, чем они стоят теперь.

Теперь рассмотрим случай, когда на счет в банке положена сумма, но в конце года к ней прибавится еще некоторая сумма, например 5 млн. руб.

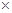
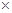
Пусть первоначальная сумма равняется 10 млн. руб. и ставка — 10%. В конце 1-го года получим FV₁ = 10 млн. (1,1) + 5 млн. = 16 млн. руб. В конце 2-го года: FV₂ = 16 млн. (1,1) + 5 млн. = 22,6 млн. руб.

Общая формула определения будущей стоимости при регулярных равных платежах или денежных поступлениях имеет следующий вид:

где Х₀ — первоначальный депозит (вклад); x — ежегодное приращение.

Данный принцип расчета получил название постоянного аннуитета или постоянной финансовой ренты. Аннуитет — это несколько равновеликих поступлений к первоначальной сумме (или выплат из первоначальной суммы), производящихся в течение ряда лет (периодов). Когда из первоначальной суммы производятся выплаты, имеет место получение финансовой ренты.

Пример:

Предположим, вам досталось по наследству 10 000 долл. и вы хотите иметь стабильный в течение 10 лет доход. Некая страховая компания предлагает такие аннуитеты из расчета 5% годовых. Какова будет сумма вашего ежегодного дохода?

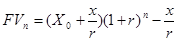
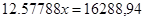
По формуле будущая стоимость FV через 10 лет будет равна 0, поскольку вся сумма должна быть вам выплачена. Мы знаем, что Х₀ = 10000 долл.; г = 0,05; n = 10. Необходимо найти х, которое будет отрицательным, поскольку это выплаты:

, следовательно x = 1295,05 долл.

Таким образом, приобретая аннуитет, вы в течение 10 лет можете получать ежегодно по 1295,05 долл.

Рассмотрим взаимосвязь будущей стоимости FV и ставки ссудного процента при различных сроках начисления. Пусть проценты выплачиваются раз в полгода. В этом случае, если 10 млн. руб. положены под 10% годовых, FV через 6 месяцев составит

млн. 500 тыс. рублей; по истечении года — млн. 25 тыс. руб.

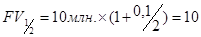
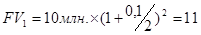
Таким образом, чем чаще выплачивается процент в течение периода t, тем больше FV на конец периода. Общая формула для расчета по истечении n лет, если проценты начисляются m раз в год, будет иметь следующее выражение:

Теперь вернемся к текущей (приведенной) стоимости и рассмотрим общее правило ее определения. Какова приведенная (текущая) стоимость капитала FV, который будет получен через n лет, если ставка составляет r% годовых?

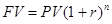
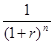
Из формулы будущей стоимости следует, что текущая стоимость равна

— коэффициент дисконтирования.

Технический прием для измерения текущей и будущей стоимости денег называется дисконтированием.

Дисконтирование — это процесс, обратный начислению сложных процентов.

Пример:

Пусть будущий доход составляет 10 млн. руб., r= 10% годовых. Какова будет дисконтированная стоимость данного дохода, если его получение ожидается через 1 год?

млн. 90 тыс. 909 руб.

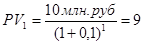
Если доход ожидается через 2 года:

млн. 264 тыс. 463 руб.

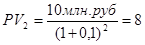
Рассмотрим еще один пример.

Пример:

Вам предлагают вложить 500 млн. руб. в строительство дома, который можно будет продать через 5 лет за 600 млн. руб. Согласитесь ли вы принять данное предложение?

Сначала определим, сколько стоит сегодня возможность получить 600 млн. руб. через 5 лет при банковской ставке 5% годовых. Иначе говоря, какую сумму следовало бы положить сегодня в банк, чтобы иметь на счете через 5 лет 600 млн. руб.? Эта сумма рассчитывается по формуле текущей стоимости

млн. 190 тыс. руб.

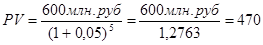
Таким образом, для получения 600 млн. руб. через 5 лет в банк следовало бы вложить 470 млн. 109 тыс. руб., что меньше суммы предполагаемых инвестиций в строительство дома (500 млн. руб.).

Теперь определим доход, который можно было бы получить при вложении 500 млн. руб. в банк на 5 лет при ставке 5% годовых. Он составит:

638 млн. 150 тыс. руб.

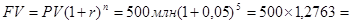
Как видим, это больше той суммы, которую можно было бы получить от продажи дома.

Для определения рентабельности (выгодности) инвестиционного проекта вычисляют чистую дисконтируемую стоимость NРV. Для этого необходимо сделать расчет будущих поступлений и выразить их в сегодняшних деньгах, после чего сопоставить дисконтированный доход с сегодняшними капиталовложениями.

В нашем случае дисконтированная стоимость будущего дохода в 600 млн. руб. составляет 470 млн. 109 тыс. руб. Сегодняшние капиталовложения I равны 500 млн. руб. Таким образом, чистая приведенная стоимость составит:

470 млн. 1 09 тыс. руб. — 500 млн. руб. = -29 млн. 891 тыс. руб.

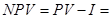
Как видим, чистая дисконтированная стоимость имеет отрицательный знак, что свидетельствует о невыгодности (убыточности) данного инвестиционного проекта. Проект будет рентабельным, если NРV> 0.

Источник

Что такое временная стоимость денег

Временная стоимость или, как ещё часто говорят, временная оценка денег (ударение в слове «временная» здесь ставится на последний слог) – это экономическая концепция учитывающая изменение стоимости денег с течением времени.

Если говорить простыми словами, то суть данной концепции можно выразить одним предложением: одна и та же сумма денег сегодня стоит дороже, чем завтра и в последующие дни (причем, чем больше промежуток времени, тем больше эта самая разница в стоимости).

Объясняется это также довольно просто, как с экономической, так и с чисто психологической точки зрения. С точки зрения человеческой психологии всегда приятнее получить деньги сегодня, нежели завтра, в следующем месяце или через год. А поэтому одна и та же сумма полученная, что называется, сей момент, всегда оценивается дороже.

Ну а с точки зрения экономики, временная стоимость денег объясняется (и, собственно, оценивается) теми процентами, которые деньги могут принести за конкретный рассматриваемый промежуток времени.

Взять, к примеру, простой вклад в банк. Если вы положили на свой банковский счёт 100000 рублей, а через год сняли с него уже 108000 рублей, то временная стоимость указанной суммы денег за этот период составила 8000 рублей (более корректно будет указать её в процентах – 8% годовых).

В общем и целом из рассматриваемой концепции вытекают два следующих важных принципа:

1. В рамках проведения любых финансовых операций (с платежами, разнесёнными по срокам) следует обязательно учитывать фактор времени при взаиморасчётах;
2. В плане анализа долгосрочных инвестиций (или финансовых операций) некорректно суммировать денежные величины, относящиеся к разным моментам времени (без учёта стоимости денег за рассматриваемые периоды).

Как рассчитать временную стоимость денег

Теперь давайте поговорим о том, как, собственно говоря, эту самую пресловутую стоимость рассчитать. Как уже понятно из вышесказанного, временная стоимость денег в численном выражении является не чем иным, как той прибылью, которую можно бы было извлечь из них (например, посредством инвестирования) за рассматриваемый период времени.

То есть в самом простом случае, например при инвестировании денег в облигации с годовой ставкой доходности в 8%, потерянная прибыль за год будет составлять эти самые 8%. Другими словами, сумма в 100000 рублей, через один год будет оцениваться уже в (100000 + 100000х0,08) = 108000 рублей. И наоборот, будущая сумма (через один год) в 100000 рублей, в настоящее время будет оценена в 100000/1,08 = 92592,59 рублей.

При проведении финансовых операций, все разнесённые во времени платежи приводят к единому моменту времени (дисконтируют). Таким образом и учитывается временная стоимость денег.

Принято различать два основных вида стоимости:

1. Нынешняя стоимость денег (Present value, PV);
2. Будущая стоимость денег (Future value, FV).

Нынешнюю стоимость денег PV ещё называют дисконтированной стоимостью. Для приведённого выше примера (100000 рублей и восьмипроцентных облигаций), нынешняя стоимость денег равна 100000 рублей, а будущая, соответственно, 108000 рублей.

В общем случае, при проведении финансовых расчётов все денежные суммы приводятся либо к PV, либо к FV (за заданный промежуток времени) и только после этого их суммируют (или проводят другие вычисления с ними).

Расчёты величин PV и FV могут проводиться как на основе простого, так и на основе сложного процента.

Напомним, что сложным процентом называется начисление прибыли с учётом реинвестирования. То есть, например, прибыль за пять лет при годовой ставке доходности в 5%, будет считаться с учётом того, что каждый год к инвестируемой сумме добавляются 5% прибыли.

В случае расчёта на основе простого процента, формулы нынешней и будущей стоимости денег будут иметь вид:

где R – процентная ставка (годовых);

T – срок в годах.

При расчёте на основе сложного процента, формулы примут вид:

А, например, для случая аннуитетных платежей со ставкой роста g и ставкой дисконтирования i, нынешнюю стоимость денег (PV) можно рассчитать по формуле:

Что оказывает влияние на временную стоимость денег

Если, что называется, копнуть чуть глубже, то можно сказать, что временная стоимость денег может зависеть как от внутренних, так и от внешних факторов. К внутренним факторам следует отнести такие, которые зависят главным образом от того, каким образом происходит распоряжение деньгами с течением времени. А именно:

1. Уровень доходности (проценты от инвестиций денежных средств);
2. Уровень риска сопряжённый с вышеупомянутыми инвестициями. Риск может заключаться как в неполучении дохода от инвестиций, так и в прямом убытке от них (вплоть до полного невозврата инвестированных средств).

К внешним же факторам относят те, которые не зависят от того каким образом управляются деньги, в какие финансовые инструменты они инвестируются и пр. Самым главным из них является инфляция. Чем выше уровень инфляции, тем больше обесцениваются деньги со временем и, следовательно, тем меньше становится их будущая стоимость (FV).

Для учёта всех этих факторов существуют сложные формулы, позволяющие максимально точно (насколько это вообще возможно) рассчитать временную стоимость денег. Точность таких расчётов во многом ограничена тем, что такие величины как уровень доходности, риск или инфляция берутся исходя из прогнозируемых значений (а любой прогноз имеет свою степень погрешности).

Мы же не стали вникать в такие премудрости и привели простые формулы для расчёта текущей (PV) и будущей (FV) стоимости денег на основе предполагаемого уровня доходности по ним (см. предыдущий раздел). Полагаю, что этого вполне достаточно для того, чтобы понять всю суть излагаемой здесь теории.

Ну а если сказать ещё проще, то с точки зрения простого трейдера или инвестора, рассматриваемая концепция временной стоимости денег может быть сведена к аксиоме: Деньги должны делать деньги.

Источник