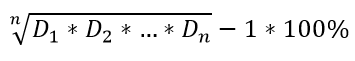- Требуемая доходность | Required Rate of Return
- Модель оценки капитальных активов CAPM
- Подход на основе дисконтирования дивидендов
- Требуемая доходность в корпоративных финансах
- Дисконтирование денежных потоков
- Выводы
- Как считать доходность инвестиций: формулы расчета
- Как рассчитать доходность инвестиций?
- Как считать доходность в процентах годовых?
- Как считать среднегодовую доходность
- Как рассчитать среднюю годовую доходность, если известны доходности по годам?
- Рассчитываем доходность облигаций с дисконтом и премией
- Виды доходности облигаций
- Дисконтная
- Купонная
- Текущая (CY, current Yield)
- Номинальная
- К погашению
- Простая
- Эффективная (YTM, Yield TO Matutity)
- Как рассчитать доходность дисконтной облигации или с премией?
Требуемая доходность | Required Rate of Return
Требуемая доходность или требуемая ставка доходности (англ. Required Rate of Return) является одним из ключевых показателей, который широко используется в инвестиционной сфере и корпоративных финансах. В общем виде эту экономическую категорию можно определить как минимальную процентную ставку, под которую инвестор будет согласен осуществить вложение своих средств. Чтобы определить ее, необходимо принять во внимание безрисковую процентную ставку, доходность рыночного портфеля, риск инфляции, риск ликвидности и прочие факторы. В корпоративных финансах требуемая ставка доходности используется для оценки инвестиционных проектов и анализа дисконтированных денежных потоков. Поскольку этот показатель используется в разных сферах, методика его расчета и использования имеет существенные различия, которые следует рассмотреть более подробно.
Модель оценки капитальных активов CAPM
Одним методов оценки требуемой ставки доходности при осуществлении инвестиций в акции является модель оценки капитальных активов (англ. Capital Asset Price Model, CAPM), которая выглядит следующим образом:
где ki – требуемая ставка доходности для i-ой акции;
KRF – безрисковая процентная ставка;

(Подробнее о модели CAPM можно прочитать здесь)
Подход на основе дисконтирования дивидендов
Оценка требуемой доходности акций также может производиться на основе концепции дисконтирования денежных потоков, которые возникают в результате выплаты дивидендов. В общем виде модель постоянного роста дивидендов можно представить следующим образом:
где P0 – текущая рыночная цена акции;
D1 – ожидаемый размер дивиденда;
ke – требуемая ставка доходности;
g – темп прироста дивидендов.
Таким образом, формула расчета требуемой ставки доходности будет выглядеть так:
(Подробнее о модели постоянного роста дивидендов можно прочитать здесь)
Требуемая доходность в корпоративных финансах
Практическое применение такого показателя как требуемая доходность распространяется не только на оценку инвестиционных решений о вложении средств в акции. Корпорации постоянно сталкиваются с необходимостью оценки различных инвестиционных проектов, не связанных с вложениями в ценные бумаги, например, расширение производственных возможностей, выход на новые рынки сбыта или запуск новых видов продукции. В этом случае требуемая ставка доходности для реализации такого проекта будет равна средневзвешенной стоимости капитала корпорации (англ. Weighted Average Cost of Capital, WACC).
Формула расчета этого показателя выглядит следующим образом:
где wd – удельный вес заемного капитала;
kd – стоимость заемного капитала;
kce – стоимость обыкновенного акционерного капитала;
kpe – стоимость привилегированного акционерного капитала;
T – ставка корпоративного налога на прибыль.
Дисконтирование денежных потоков
Помимо всего вышеперечисленного, требуемая ставка доходности также нашла широкое применение и в других моделях, основывающихся на принципе дисконтирования денежных потоков, в частности для:
- расчета чистой приведенной стоимости инвестиционного проекта;
- расчета настоящей стоимости свободного денежного потока для оценки рыночной стоимости корпорации.
Выводы
Методика оценки требуемой ставки доходности является достаточно сложной в практическом применении, поскольку может основываться на различных методических подходах. Также процесс ее оценки затруднен тем, что аналитику необходимо учитывать большое количество прочих факторов, таких как инфляция, ликвидность, деловая активность и т.д., которые влияют на рыночную стоимость активов. Однако правильная оценка требуемой доходности позволит выбрать правильные инвестиционные решения.
Источник
Как считать доходность инвестиций: формулы расчета
Автор: Алексей Мартынов · Опубликовано 01.06.2015 · Обновлено 05.11.2015

Доходность (норма доходности, уровень доходности) — это степень увеличения (или уменьшения) инвестированной суммы за определенный период времени. В отличие от дохода, который выражается в номинальных величинах, то есть в рублях, долларах или евро, доходность выражается в процентах. Доход можно получать в двух видах:
- процентный доход — это проценты по депозитам, купоны по облигациям, дивиденды по акциям, арендная плата по недвижимости;
- рост стоимости купленных активов — когда цена продажи актива больше цены покупки — это акции, облигации, недвижимость, золото, серебро, нефть и другие товарные активы.
Такие активы как недвижимость, акции и облигации могут сочетать в себе два источника дохода. Расчет доходности нужен для оценки роста или падения вложений и является критерием оценки эффективности инвестиций.
Как рассчитать доходность инвестиций?
В общем виде доходность всегда рассчитывается как прибыль (или убыток), деленная на сумму вложенных средств, умноженная на 100%. Прибыль считается как сумма продажи актива — сумма покупки актива + сумма денежных выплат, полученных за период владения активом, то есть процентный доход.
Формула 1
Мы купили акцию по цене 100 рублей (сумма вложений), продали акцию по цене 120 рублей (сумма продажи), за период владения акцией получили 5 рублей дивидендов (денежные выплаты). Считаем доходность: (120-100+5)/100 = 0,25 ∗ 100% = 25%.
Формула 2
Есть вторая формула, по которой доходность считается как сумма продажи актива + сумма денежных выплат, деленная на сумму вложений, минус 1, умноженная на 100%.
Как считать доходность в процентах годовых?
В формуле расчета простой доходности не учитывается такой важный параметр, как время. 25% можно получить за месяц, а можно и за 5 лет. Как тогда корректно сравнить доходность активов, время владения которыми различается? Для этого считают доходность в процентах годовых. Доходность в процентах годовых рассчитывается для того, чтобы сравнить друг с другом эффективность активов, время владения которыми отличается. Доходность в процентах годовых — это доходность, приведенная к единому знаменателю — доходности за год.
К примеру банковский вклад дает 11% в год, а какие-то акции принесли 15% за 1,5 года владения ими, что было выгоднее? На первый взгляд акции, они ведь принесли доходность больше. Но инвестор владел ими больше на полгода, поэтому их доходность как бы растянута во времени по сравнению с депозитом. Поэтому, чтобы корректно сравнить депозит и акции, доходность акций нужно пересчитать в процентах годовых.
Для этого в формулу добавляется коэффициент 365/T, где Т — количество дней владения активом.
Мы купили акцию за 100 рублей, продали через 1,5 года за 115 рублей. 1,5 года это 1,5*365=547 дней.
(115-100)/100 ∗ 365/547 ∗ 100% = 10%. В этом случае депозит оказался немного выгоднее акций.
Как форекс, управляющие компании, брокеры и банки манипулируют годовой доходностью.
В любой рекламе доходности обращайте внимание на сноски, уточняйте какую доходность указывают в рекламе и за какой период. К примеру, в рекламе звучит доходность 48% годовых. Но она может быть получена всего лишь за один месяц. То есть компания за месяц заработала 4% и теперь с гордостью рекламирует продукт, дающий 4*12=48% годовых. Даже вы, заработав за день на бирже 1%, можете хвастаться, что заработали 365% годовых) Только доходность эта виртуальная.
 Как считать среднегодовую доходность
Как считать среднегодовую доходность
Срок владения активами может составлять несколько лет. При этом большинство активов не растет на одну и ту же величину. Такие активы как акции могут падать или расти на десятки или сотни процентов в год. Поэтому хочется знать, сколько в среднем в год росли ваши инвестиции. Как тогда вычислить среднюю годовую доходность? Среднегодовая доходность рассчитывается через извлечение корня по формуле:
Формула 1
где n — количество лет владения активом.
3√125/100 — 1 ∗ 100% = 7,72%
Формула 2
Другая формула расчета среднегодовой доходности — через возведение в степень.

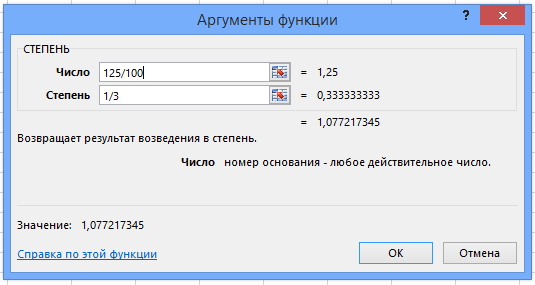
Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Если известны доходности актива по годам, то среднюю годовую доходность можно вычислить перемножив годовые доходности и извлечь из произведения корень в степени равной количеству лет.
Для начала переведите доходности из процентов в числа.
Эти формулы учитывают эффект сложных процентов. Простая формула расчета доходности этого не учитывает и завышает доходность, что не совсем правильно.
Источник
Рассчитываем доходность облигаций с дисконтом и премией
В последнее время интерес к покупке облигаций растет среди населения, поскольку доход от них может быть выше, чем от вкладов по депозиту. О разновидностях доходности ценных долговых бумаг, а также о том, как определить прибыль от приобретённых активов с премией или дисконтом, рассказано в статье.
Виды доходности облигаций
Для оценки прибыльности долговых бумаг используют показатель, определяющий доход от облигаций в годовых процентах (так называемый купонный), который будет получать владелец актива. Это и есть доходность. А разница, полученная от продажи облигаций, приобретенных ранее по более низкой цене, называется дисконтной доходностью. Теперь об этом подробнее.
Дисконтная
Дисконтная прибыль образуется из разницы между ценой, по которой биржа предлагает приобретение долговой бумаги, и суммой стоимости облигации по номиналу, получаемой вкладчиком при погашении.
Пример: номинал бумаги равен 1 000 рублям, и её приобрели за 850, то доходность составит:
1 000 − 850 = 150 (рублей), или 17,6 %.
Купонная
При купонной форме выплаты дохода инвестор приобретает облигацию по номинальной цене, а затем раз в год, в полгода или в квартал, в заранее оговоренную дату, получает прибыль в виде так называемого купона, сумма которого составляет определённый годовой процент.
Справка. Начисление купона осуществляется ежедневно, а выплата денег — строго в назначенную дату.
Например, облигация стоит 1 000 рублей. Если купонный доход составляет 20 % в год, а выплаты производятся ежеквартально, то один раз в квартал вкладчик получит:
20 : 4 = 5 (%), или 50 рублей.
В случае досрочной продажи облигации продавец, помимо номинала, получает от покупателя НКД (накопившийся купонный доход), сумма которого складывается из ежедневно начисляемых, но ещё не выплаченных процентов.
Текущая (CY, current Yield)
Эта разновидность доходности подобна оформленному в банке депозитному вкладу и показывает сумму прибыли за текущий купонный период, вне зависимости от того, каков срок обращения облигации, а также как за это время варьировалась её стоимость.
Рассчитывают данный показатель следующим образом:
текущая доходность (%) = выплаты по купону: цена покупки бумаги без НКД × 100.
Актив с номиналом 1 000 рублей приобретен на бирже по цене 1 200 рублей (120 % от номинала) и приносит 100 рублей купонного дохода. При номинальной цене облигации это составило бы 10 % годовых, а при рыночной получается:
100 : 1 200 × 100 = 8,3 (%).
Номинальная
Доходность, которую рассчитывают, исходя из общей суммы полученных купонов, называют номинальной. Так, например, если при номинальной стоимости актива в 1 000 рублей его владелец дважды в год получил по 50 рублей (всего 100 рублей), то номинальная доходность облигации составляет:
100 × 100 : 1000 = 10 (%).
К погашению
Доходность к погашению показывает прибыль вкладчика от каждого вложенного рубля и бывает двух видов:
- простая, при которой полученная прибыль не вкладывается снова в долговые бумаги;
- эффективная, предполагающая повторное вложение выплат по купонам в облигации в соответствии с изначальной процентной ставкой.
Простая
Такая разновидность доходности к погашению включает в себя всю прибыль, которую вкладчик получает за период владения облигациями:
- выплаты по купонам;
- возвращение номинальной стоимости долговых бумаг в момент их погашения.
Внимание! В случае приобретения ценной бумаги по цене ниже номинальной прибыль владельца в конечном итоге будет выше. При цене покупки с превышением номинала размер дохода снизится.
Формула, по которой производится расчёт, достаточно сложна:
Ys (простая доходность) = (Ʃ(Сi (размер купона) + Ni (размер выплаты номинала, с учётом амортизации, оферты и погашения) − Pd (цена покупки бумаги с учётом НКД) : Pd) × (В (количество дней в году) : (ti (дата выплаты купонного платежа) − t0 (текущая дата)).
Эффективная (YTM, Yield TO Matutity)
Эффективную доходность к погашению возможно показать только в том случае, если весь купонный доход от актива снова вкладывается в долговые бумаги, причём по той же процентной ставке, по которой была совершена изначальная покупка.
Вложенная прибыль от купонов приносит новый доход за счёт того, что на неё также начисляются проценты.
Справка. На фондовых рынках по эффективной доходности определяют, насколько прибыльно инвестировать в те или иные бумаги, имеющие разные сроки обращения и купоны, а также стоимость выше или ниже номинала.
Расчёт производится по очень сложной формуле. Для того чтобы он был максимально точным, рекомендуется пользоваться специальными калькуляторами на профильных сайтах, отталкиваясь именно от той цены, по которой была совершена покупка.
Как рассчитать доходность дисконтной облигации или с премией?
Разбег между номиналом долговой бумаги и реальной (рыночной) ценой её покупки определяет, приобретён ли актив с дисконтом или с премией.
В первом случае продажа производится по цене ниже номинальной (дисконт), а во втором — выше (премия).
Наличие разрыва между номиналом (то есть той суммой, которую вкладчик получит при погашении) и ценой на бирже связано с тем, что размер купона устанавливается в момент выпуска облигации, а кредитные ставки подвержены постоянным изменениям. Кроме того, может меняться и уровень доверия к заёмщику, а это также сказывается на цене активов.
Для того чтобы скомпенсировать перемены, стоимость бумаг соответственно снижают или повышают.
Если, к примеру, облигация была выпущена с доходностью в 12 % годовых, а в результате изменений на рынке нормальная ставка стала составлять 8 %, и спрос на бумагу вырос, её переоценят, и стоимость станет выше на 12 − 8 = 4 (%). Значит, такая облигация будет продаваться с премией в 4 % от номинала, что соответствует разнице между рыночным и купонным процентом.
Если же бумагу выпустили с доходностью 4 %, что намного ниже рыночной, то её продажа будет осуществляться по стоимости ниже номинальной, то есть с дисконтом, размер которого должен быть таким, чтобы обеспечить прибыль от вложений, соответствующую той, что можно получить при инвестировании в иные подобные активы.
Для расчёта текущей доходности облигации, приобретённой с дисконтом или с премией, выводят так называемую текущую модифицированную или скорректированную доходность. Считают её так:
текущая доходность (%) + (100 − цена покупки в % от номинала без учёта НКД): номинальная стоимость в %, то есть 100 %.
Например, при покупке бумаги за 120 % от номинала с купонным доходом 100 рублей в год доходность составляет:
100 : 1 200 × 100 = 8,3 (%) — текущая;
8,3 + (100 − 120) : 100 = 8,3 − 0,2 = 8,1 (%) — модифицированная.
Показатель текущей доходности облигации, купленной с премией (наценкой), снизился.
Если же актив приобрели за 85 % от номинала и с купоном 100 рублей, то:
100 : 85 × 100 = 11,7 % — текущая;
11,7 + (100 − 85) : 100 = 11,7 + 0,15 = 11,85 (%) — скорректированная.
Показатель текущей доходности облигации, купленной с дисконтом (по цене ниже номинала), стал выше.
Примеры быстрого приблизительного расчёта простой доходности к погашению при покупке бумаг с премией и с дисконтом:
- Вкладчик совершил покупку за 120 % от номинальной стоимости (премия) и с купоном 150 рублей:
- текущая доходность составляет: 150 : 1 200 × 100 = 12,5 % в год;
- при условии погашения через год инвестор получит: 1 000 (номинал) + 150 (купон) = 1 150 (рублей);
- получается убыток при погашении: 1 200 − 1 150 = 50 (рублей), что составляет: 50 × 100 : 1 200 = 4,1 % потерь за год;
- на величину этого процента уменьшают текущую доходность и получают итоговую к погашению: 12,5 − 4,1 = 8,4 (%).
Важно! При сроке погашения, превышающем 1 год, разница между номинальной и реальной ценой покупки распределяется на всё число лет, в результате чего годовая доходность будет тем выше, чем дольше период, по истечении которого долговые бумаги погасятся.
- Напротив, облигации, приобретённые по цене ниже номинала (дисконт), принесут тем большую прибыль, чем короче срок их погашения:
- так, например, бумага, купленная за 85 % от номинальной стоимости и с купоном 110 рублей, через год доставит: ((1 000 − 850 + 110) × 100) : 850 = 30,5 %;
- при более длительном сроке погашения годовая доходность будет снижаться.
Приобретение облигаций может стать для граждан достойным источником дополнительного дохода. Чтобы покупка была удачной, нужно рассмотреть все параметры ценных бумаг, при этом обращая особое внимание на их доходность, некоторые виды которой несложно рассчитать самостоятельно. А для более серьёзных расчётов можно воспользоваться услугами специализированных сайтов.
Подпишитесь на нашу рассылку, и каждое утро в вашем почтовом ящике будет актуальная информация по всем рынкам.
Источник



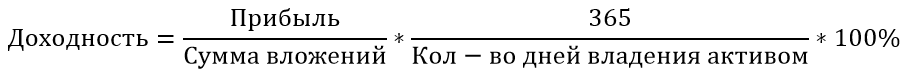
 Как считать среднегодовую доходность
Как считать среднегодовую доходность