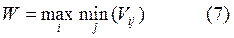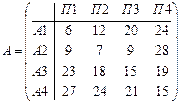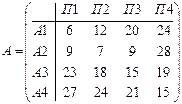Транспортное предприятие должно определить уровень своих

Основы теории принятия решений в условиях неопределенности и риска

В условиях неопределенности (недостатка информации) внешняя среда («природа») может находиться в одном из множества конечных состояний. Поэтому принятие решений в условиях неопределенности часто называют «игры с природой».

Пусть S_i – состояние природы, которое меняется m раз (от 1 до m). Все состояния известны. Неизвестно только какое состояние будет иметь место в условиях, когда планируется реализация управленческого решения. Будем считать, что множество управленческих решений (планов) R_j – конечно и равняется n.

Реализация плана R_j когда природа находится в состоянии S_i приводит к одному из следственных результатов:

1. Выигрышу от принимаемого решения (плана);

Исходные данные для таких задач задаются в виде матрицы, строки которой соответствуют управленческим решением R_{j ,} а столбцы — состояниям природы S_i .

V_ij – результат (выигрыши или проигрыши). В качестве результатов в отдельных задачах используется матрица рисков.

Риск – это мера несоответствия между разными возможными рультатами от принятия решений. Элементы матрицы рисков связаны с элементами матрицы выигрышей следующим соответствием:

где r_ij – элемент матрицы рисков

V_ij – элемент матрицы выигрышей.

Если матрица результатов V_ij представляет собой матрицу потерь, то элементы матрицы рисков r_ij рассчитывается следующим образом:

Для принятия решений в условиях неопределенности используют критерии Лапласа, Вальда, Севиджа, Гурвица.

Критерий Лапласапредполагает все состояния природы равновероятными, т.е. каждому состоянию S_i ставится вероятность q_i, определяемая по формуле:

q_i= ,

где n — количество состояний природы S_i

При этом выбирается действие, дающее наибольший ожидаемый выигрыш:

,

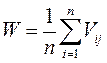
где W –значения критерия Лапласа.

Оптимальная стратегия выбирается по максимальному значению W. Если в исходной задаче дана матрица рисков r_ij, то оптимальную стратегию выбирают по минимальному значению W.

Пример. Транспортное предприятие должно определить уровень своих провозных возможностей, так чтобы удовлетворить спрос на транспортные услуги. Спрос точно не известен, но прогнозируется, что он может принимать 1 из 4-х значений.

Для каждого уровня спроса существует наилучший уровень провозных возможностей, отклонение от которых проводят к дополнительным затратам. Определить оптимальный вариант провозных возможностей по данным следующей таблицы:

Варианты провозных возможностей

Затраты по вариантам спроса на транспортные услуги, млн. р.

Применим критерий Лапласа

V_ij – матрица потерь

S1 S2 S3 S4

R1 V= R2 R3 R4

q_i = 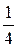= 0,25

Так как дана матрица потерь, то выбираем W с наименьшим значением. Т.о. наилучшая стратегия развития провозимых возможностей 2.

Критерий Вальда.Если в исходной матрице результат V_ij представляет собой потери, то при выборе оптимальной стратегии используют минимаксный критерий:

Если V_ij элементы матрицы выигрышей, то используемых максиминный критерий:

Пример 4. Используя условия примера 3 выбрать оптимальную стратегию с помощью критерия Вальда.

max (6; 12; 20; 24 ) =24

max (9; 7; 9; 28) =28

max (23; 18; 15; 19 ) =23

max (27; 24; 21; 15) =27

W = min (24; 28; 23; 27) =23

В соответствии с критерием Вальда наилучшей стратегий будет 3.

Критерий Севиджа.Используется только для матрицы рисков, поэтому если даны матрицы выигрышей или потерь, то их необходимо пересчитать в матрицу рисков по формулам (6) или (7).

Пример 5. Для исходных данных примера 3 применим критерий Севиджа.

Источник

Решение. Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на

Контрольный пример

Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но прогнозируется, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия. Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Возможные прогнозируемые затраты на развитие провозных возможностей представлены в табл.4.1.

Варианты провозных возможностей транспортного предприятия

Варианты спроса на транспортные услуги

Необходимо выбрать оптимальную стратегию. Использовать: критерий Вальда, критерий Сэвиджа, критерий Гурвица.

Имеются четыре варианта спроса на транспортные услуги, что равнозначно наличию четырех состояний «природы»: П1, П2, П3, П4. Известны так же четыре стратегии развития провозных возможностей транспортного предприятия: А1, А2, А3, А4. Затраты на развитие провозных возможностей при каждой паре П_i и А_i заданы следующей матрицей:

Построим матрицу рисков. В данном примере a_ij представляет затраты т.е. потери значит для построения матрицы рисков используется принцип r_ij = a_ij — b_j, где b_j = min a_ij.

Источник

Решение. Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на

Контрольный пример

Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но прогнозируется, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия. Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Возможные прогнозируемые затраты на развитие провозных возможностей представлены в табл.4.1.

Варианты провозных возможностей транспортного предприятия

Варианты спроса на транспортные услуги

Необходимо выбрать оптимальную стратегию. Использовать: критерий Вальда, критерий Сэвиджа, критерий Гурвица.

Имеются четыре варианта спроса на транспортные услуги, что равнозначно наличию четырех состояний «природы»: П1, П2, П3, П4. Известны так же четыре стратегии развития провозных возможностей транспортного предприятия: А1, А2, А3, А4. Затраты на развитие провозных возможностей при каждой паре П_i и А_i заданы следующей матрицей:

Построим матрицу рисков. В данном примере a_ij представляет затраты т.е. потери значит для построения матрицы рисков используется принцип r_ij = a_ij — b_j, где b_j = min a_ij.

Источник

Контрольная работа по предмету «Системный анализ в экономике» (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

Определим средний ожидаемый выигрыш:

· для вершины 1 ОДО1 = 0,5 * 300 000 + 0,5 * (-150 000) = 75 000 руб.;

· для вершины 2 ОДО2 = 0,5 * 250 000 + 0,5 * (-70 000) = 90 000 руб.;

· для вершины 3 ОДО3 = 0,5 * 100 000 + 0,5 * (-10 000) = 45 000 руб.;

Вывод. Наиболее целесообразно выбрать стратегию а2, т. е. выпускать лечебную косметику, а ветви (стратегии) а1 и а3 дерева реше­ний можно отбросить. ОДО наилучшего решения равна 90 000 руб.

Усложним рассмотренную выше задачу. Перед тем как принимать решение о виде продукции, руководство компании должно определить, заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая услуга обойдется компании в 15 000 рублей. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей.

Относительно фирмы, которой можно заказать прогноз, извест­но, что она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в виде ус­ловных вероятностей благоприятности и неблагоприятности рынка сбыта представлены в табл.3.3.

Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73.

Предположим, что фирма, которой заказали прогноз состояния рынка, утверждает:

· ситуация будет благоприятной с вероятностью 0,4;

· ситуация будет неблагоприятной с вероятностью 0,6.

На основании дополнительных сведений можно построить новое дерево решений (рис. 3.3), где развитие событий происходит от кор­ня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным.

Определим средний ожидаемый выигрыш:

· для вершины 4 ОДО4 = 0,78 * 300 000 + 0,22 * (-150 000) = 201 000 руб.;

· для вершины 5 ОДО5 = 0,78 * 250 000 + 0,22 * (-70 000) = 179 600 руб.;

· для вершины 6 ОДО6 = 0,78 * 100 000 + 0,22 * (-10 000) = 75 800 руб.;

· для вершины 7 ОДО7 = 0,27 * 300 000 + 0,73 * (-150 000) = -28 500 руб.;

· для вершины 8 ОДО8 = 0,27 * 250 000 + 0,73 * (-70 000) = 16 400 руб.;

· для вершины 9 ОДО9 = 0,27 * 100 000 + 0,73 * (-10 000) = 19 700 руб.;

· для вершины 10 ОДО10 = 0,4 * 201 000 + 0,6 * (-19 700) = 68 580 руб.;

· Необходимо проводить дополнительно, исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение.

· Ели фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно производить декоративную косметику (ожидаемая максимальная прибыль 201 000 рублей), если прогноз неблагоприятный – бытовую химию (ожидаемая максимальная прибыль 19 700 рублей).

Рис. 3.3. Дерево решений при дополнительном обследовании рынка

Задача №4
Принятие решений в условиях неопределенности.

Игры с природой

Цель работы: освоить и закрепить практические навыки по принятию и обоснованию управленческих решений в условиях недостатка информации, когда одним из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы».

Краткие теоретические сведения

Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игрок1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально.

Матрица игры с природой А = ||аij||, где аij – выигрыш (потеря) игрока 1 при реализации его чистой стратегии i и чистой стратегии j игрока 2 (i=1, …, m; j=1,…,n).

Мажорирование стратегий в игре с природой име­ет определенную специфику: исключать из рассмотрения можно лишь доминируемые стратегии игрока 1: если для всех g=1,…, n akj £ alj, k, l = 1,…,m, то k-ю стратегию принимающего решения иг­рока 1 можно не рассматривать и вычеркнуть из матрицы игры. Столбцы, отвечающие стратегиям природы, вычеркивать из матри­цы игры (исключать из рассмотрения) недопустимо, поскольку при­рода не стремится к выигрышу в игре с человеком, для нее нет це­ленаправленно выигрышных или проигрышных стратегий, она дей­ствует неосознанно.

Рассмотрим организацию и аналитическое представление игры с природой. Пусть игрок 1 имеет m возможных стратегий: А1,А2, … , Аm, а у природы имеется n возможных состояний (стратегий): П1, П2, . Пn, тогда условия игры с природой задаются матрицей А выигрышей (потерь) игрока 1:

Возможен и другой способ задания матрицы игры с природой: не в виде матрицы выигрышей (потерь), а в виде так называемой матрицы рисков R = ||rij||m, n. Величина риска — это размер платы за отсутствие информации о состоя­нии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей (потерь) А.

Риск — это разность между результатом, ко­торый игрок мог бы получить, если бы он знал действительное состоянием среды и результатом, который игрок получит при j-ой стратегии.

Зная состояние природы (стратегию) Пj, игрок выбирает ту стра­тегию, при которой его выигрыш максимальный или потеря минимальна, т. е.

rij = bj-aij, где bj = max aij, при заданном j. 1£ i £m если аij — выигрыш

rij = aij — bj, где bj = min aij, при заданном j. 1£ i £m если аij – потери (затраты)

Неопределенность, связанную с полным отсутствием информа­ции о вероятностях состояний среды (природы), называют «безна­дежной».

В таких случаях для определения наилучших решений исполь­зуются следующие критерии: Вальда, Сэвиджа, Гурвица.

Критерий Вальда. С позиций данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник.

Если в исходной матрице по условию задачи результат aij представляет выигрыш лица, принимающего решение, то выбирается решение, для кото­рого достигается значение W = max min aij, 1£ i £m, 1£ j £n – максиминный критерий.

Если в исходной матрице по условию задачи результат aij представляет потери лица, принимающего решение, то выбирается решение, для кото­рого достигается значение W = min max aij, 1£ i £m, 1£ j £n – минимаксный критерий.

В соответствии с критерием Вальда из всех самых неудачных результатов выбирается лучшей. Это перестраховочная по­зиция крайнего пессимизма, рассчитанная на худший случай.

Критерий минимаксного риска Сэвиджа. Выбор стратегии ана­логичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей А, а матрицей рисков R:

S = min max rij 1£ i £m, 1£ j £n.

Применение критерия Сэвиджа позволяет любыми путями избежать большого риска при выборе стратегии, а значит, избежать большего проигрыша (потерь).

Критерий пессимизма-оптимизма Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым сред­ним результатом, характеризующим состояние между крайним пес­симизмом и безудержным оптимизмом.

Критерий основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятность (1-р) и в самом выгодном состоянии с вероятностью р, где р – коэффициент пессимизма.

Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением:

HA = max í p max aij + (1-p) min aij ý , 1£ i £m, 1£ j £n. если aij – выигрыш

HA = min í p min aij + (1-p) max aij ý , 1£ i £m, 1£ j £n. если aij – потери (затраты)

При p = 0 критерий Гурвица совпадает с критерием Вальда. При p = 1 приходим к решающему правилу вида max max aij, к так называемой стратегии «здорового оптимизма», критерий максимакса.

Применительно к матрице рисков R критерий пессимизма-оп­тимизма Гурвица имеет вид:

HR = min íp max rij + (1-p) min rijý , 1£ i £m, 1£ j £n.

При р = 0 выбор стратегии игрока 1 осуществляется по условию наименьшего из всех возможных рисков (min rij); при р = 1 – по критерию минимаксного риска Сэвиджа.

Значение р от 0 до 1 может определяться в зависимости от склонности лица, принимающего решение, к пессимизму или оптимизму. При отсутствии ярко выраженной склонности р = 0,5 представляет наиболее разумный вариант.

В случае, когда по принятому критерию рекомендуются к ис­пользованию несколько стратегий, выбор между ними может де­латься по дополнительному критерию. Здесь нет стандартного подхода. Выбор может зависеть от склонности к риску игрока1.

Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но прогнозируется, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия. Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Возможные прогнозируемые затраты на развитие провозных возможностей представлены в табл.4.1.

Источник