Расчет рыночной доходности
Формула расчета рыночной доходности
Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.
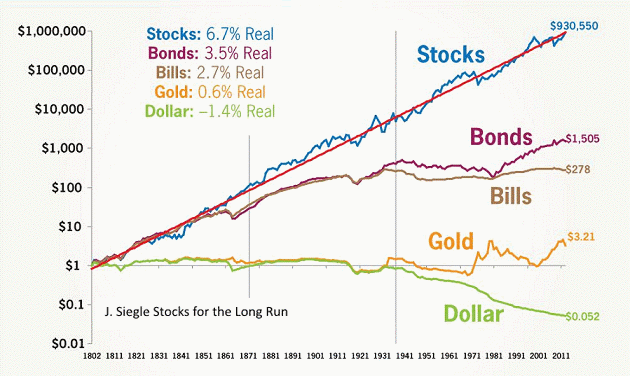
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):
Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.
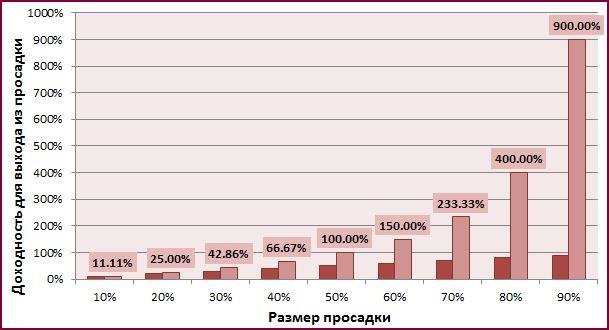
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:
Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.
В общем случае формула доходности выглядит так:
A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1
- A(0) – исходное количество денег
- А(n) – количество денег через n лет
- X – годовая доходность (в процентах)
Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то
A(n) = A(n-1) × Y = A(0) × Y^n
Задача
Актив растет на 10% в год. Какова будет его доходность через 2 года?
Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу
А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)
Обратная задача
Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):
Снова принимая нашу первоначальную доходность за условную единицу, считаем:
Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%
Задача 2
За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?
Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%
Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).
Задача 3
За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?
2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда
Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%
Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.
Задача 4
Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?
Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%
Задача 5
Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.
2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%
Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:
1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)
И средняя инфляция
Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%
P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.
Задача 6
Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?
Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.
Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.
Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).
Задача 7
Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.
Y = [(7.2 + (135-120))/120] × 100% = 18.5%
Задача 8
По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:
Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%
Источник
Что такое текущая доходность облигации
Доходность облигации — одна из самых важных характеристик ценной бумаги. Нельзя забывать, что эта величина связана со степенью риска. Чем рискованнее актив, тем выше его доходность. Это своего рода вознаграждение инвестора за тот риск, который он на себя возлагает. Существует несколько видов прибыльности облигаций. Один из них — текущая доходность.
Понятие текущей доходности облигации
Текущая доходность — это отношение суммарного купонного дохода за год к текущей стоимости ценной бумаги. Она позволяет оценить выплаты, полученные от эмитента, без учета рыночной стоимости актива и срока его обращения.
Данный показатель часто используется для сравнения прибыльности ценных бумаг разного выпуска. На него не влияет разница между ценами облигации, зафиксированными в момент ее покупки и продажи или погашения, а также прибыль от реинвестирования купонного дохода.
Текущая доходность в процентах годовых обозначается как CY.
Внимание! Для дисконтных ценных бумаг данный показатель рассчитывается путем деления дисконта на разницу между номиналом и дисконтом.
Модифицированная текущая доходность облигации
Текущая модифицированная доходность — это показатель прибыльности ценной бумаги с учетом дохода, полученного как в виде купона, так и от курсовой разницы стоимости актива.
Данная величина обозначается как ACY.
Внимание! И текущая, и модифицированная текущая доходность рассчитываются и публикуются большинством ресурсов, посвященных рынку облигаций.
Формула расчета текущей доходности
CY = C / P × 100 %, где:
C — совокупный доход по купону за год;
P — текущая рыночная стоимость актива без НКД.
Внимание! Суммарный купонный доход можно рассчитать как произведение номинальной стоимости ценной бумаги и ставки годового купонного дохода.
ACY = CY + (100 % — P %) / N %, где:
P — чистая стоимость ценной бумаги (без НКД) в процентах от номинала;
N — номинальная цена актива.
Пример расчета
Рекомендуется более подробно ознакомиться с принципами расчета CY на примере ОФЗ-46020-АД с номиналом 1 000 рублей.
- купон: 6,9 % годовых;
- рыночная цена: 870,36 рубля или 87,036 %.
CY = 6,9 / 87,036 × 100 = 7,93%.
В рассмотренном примере рыночная цена актива ниже его номинала. Поэтому CY в данном случае выше купонного процента. Если цена облигации будет расти, то и ее текущая стоимость будет меняться. Это плавающая величина.
Например, если рыночная стоимость достигнет 900 рублей или 90 %, то
CY = 6,9 /90 × 100 = 7,67 %.
Внимание! С ростом стоимости облигации ее доходность снижается, и наоборот.
Пример расчета ACY для той же ценной бумаги:
ACY = 7,93 % + (100% — 87,035 %) / 100 % = 8,69 %.
Далее рекомендуется рассмотреть на примере, как выбрать облигацию из двух предлагаемых вариантов, используя расчет CY.
Показатели первой ценной бумаги (А):
- номинальная стоимость — 1 000 рублей;
- рыночная цена — 1 050 рублей;
- ставка годового купонного дохода — 5 %.
Показатели второй облигации (Б):
- номинальная стоимость — 5 000 рублей;
- рыночная цена — 5 500 рублей;
- ставка годового купонного дохода — 5 %.
CY (А) = 5 / 105 × 100 = 4,7 %.
CY (Б) = 5 / 550 × 500 = 4,5 %.
Из расчетов видно, что прибыльность первой облигации выше, чем аналогичный показатель второй ценной бумаги. Следовательно, выбирая между двумя активами, если все другие условия равны, покупка первого варианта может быть предпочтительнее.
Разные виды доходности облигаций позволяют оценить финансовую выгоду от инвестиций в ценные бумаги с использованием разных параметров. Выбор величины для анализа зависит от тех целей, которые преследует трейдер, вкладывая свой капитал в активы. Если задача инвестора заключается в эффективном инвестировании сроком на один год, рекомендуется при выборе инструментов для вложений ориентироваться на максимально высокий показатель CY. При покупке активов по цене, отличной от номинала, более важной является оценка модифицированной доходности.
Подпишитесь на нашу рассылку, и каждое утро в вашем почтовом ящике будет актуальная информация по всем рынкам.
Источник
Текущая доходность
Удобным способом сравнения нескольких ценных бумаг между собой, является их сопоставление по уровню текущей доходности (ТД). Ниже мы рассмотрим формулы для определения текущей доходности облигаций и акций. Обратите внимание на то, что сравнивать по уровню ТД, корректно лишь бумаги одного типа. То есть, акции сравниваем с акциями, а облигации — с облигациями.
В мировой финансовой практике, термин текущая доходность обычно выражается английским словосочетанием Current Yield и обозначается аббревиатурой CY.
Текущая доходность облигаций
Для процентных облигаций формула расчёта ТД выглядит следующим образом:
CY – текущая доходность облигаций (Current Yield);
S – сумма купонных платежей за год;
P0 — текущая рыночная стоимость облигации (стоимость покупки).
Сумму купонных платежей за год, можно рассчитать исходя из номинальной стоимости облигации и ставки годового купонного дохода по ней:
Pn — номинальная стоимость облигации;
C — ставка годового купонного дохода.
Давайте рассмотрим простой пример выбора из двух облигаций. Допустим есть облигация A со следующими параметрами:
- Номинальная стоимость 1000 рублей;
- Текущая рыночная стоимость 1050 рублей;
- Ставка годового купонного дохода 5%.
И облигация B, с параметрами:
- Номинальная стоимость 5000 рублей;
- Текущая рыночная стоимость 5500 рублей;
- Ставка годового купонного дохода 5%.
Рассчитаем текущую доходность для облигации A:
CY = S / P0 = (0,05 х 1000) / 1050 = 0,047 = 4,7%
И текущую доходность облигаций B:
CY = S / P0 = (0,05 х 5000) / 5500 = 0,045 = 4,5%
Как видно из проведённых расчётов, текущая доходность облигации А несколько выше аналогичного параметра для облигации В. Следовательно, при прочих равных условиях, облигация А является более предпочтительной к покупке.
Текущая доходность акций
Для акций, текущая доходность определяется исходя из их текущей рыночной цены и суммы выплаченных за год дивидендов. Её можно определить по следующей формуле:
CY — текущая доходность акций;
D – сумма дивидендов выплаченных за год;
P0 — рыночная стоимость акции.
Например акция компании A имеющая рыночную стоимость 2000 рублей, принесла за один год дивидендный доход в сумме 100 рублей. В этом случае её текущая дивидендная доходность составляет:
CY = D / P0 = 100 / 2000 = 0,05 = 5%
Дивидендный доход по акциям не является величиной постоянной, его величина зависит от многих факторов. И даже если компания завершит очередной финансовый год с хорошей прибылью, то общее собрание акционеров может всю её (за исключением ряда обязательных выплат конечно) направить на дальнейшее развитие бизнеса**. Поэтому сравнивать между собой акции двух разных компаний, по критерию текущей дивидендной доходности, хотя и можно, но такое сравнение не будет столь объективным, как, например, для облигаций.
** Это не касается привилегированных акций, по которым дивиденды гарантированы и составляют определённый фиксированный процент от прибыли.
Кроме этого, говоря об акциях, термином текущая доходность иногда называют тот процент прибыли, который может быть получен за счёт разницы их курсовой стоимости (в момент покупки и в момент продажи). В этом случае формула ТД примет следующий вид:
P0 — текущая рыночная стоимость акции;
P — цена покупки акции.
Предположим, что акционер купивший акции компании В по цене 3000 рублей, через некоторое время решил их продать по текущей рыночной цене в 3300 рублей. При этом его доход составит:
CY = (P0 – P)/P = (3300-3000) / 3000 = 0,1 = 10%
Источник