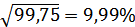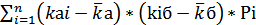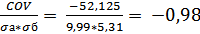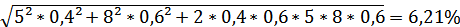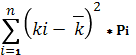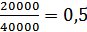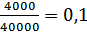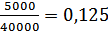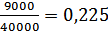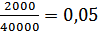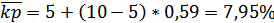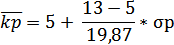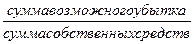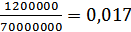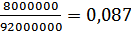Ожидаемая доходность акций
В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.
Формула
В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

где Pi – вероятность наступления i-го исхода событий;
ki – доходность при i-ом исходе событий;
n – количество исходов событий.
В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

ki – доходность ценной бумаги в i-ом периоде;
n – количество наблюдений.
Пример расчета
Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.
Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.



Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.
Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.
Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.



Источник
Статистическая величина обозначающая ожидаемую доходность актива
Управление портфелем ценных бумаг
Ожидаемая доходность портфеля
Главными параметрами управления портфелем ценных бумаг, которые необходимо определить, являются ожидаемая доходность и риск. Формируя портфель, невозможно точно определить будущую динамику его доходности и риска, поэтому инвестиционный выбор основывается на ожидаемых значениях доходности и риска. Данные величины оцениваются, в первую очередь, на основе статистической информации за предыдущие периоды времени. Так как будущее вряд ли повторит прошлое со 100%-ой вероятностью, то полученные оценки можно корректировать согласно своим ожиданиям развития конъюнктуры.
Ожидаемая доходность портфеля рассчитывается на основе ожидаемой доходности активов.Ожидаемая доходность активов определяется двумя способами. Первый состоит в том, чтобы на основе прошлых данных статистики доходности актива рассчитать ее среднеарифметическое значение по формуле: где D — ожидаемая доходность актива, r — фактическая доходность актива в i-м периоде, n — число периодов наблюдения (периоды имеют одинаковую продолжительность).
Пример. Данные о доходности актива за прошедшие 9 лет представлены в таблице.
Ожидаемая доходность актива в расчете на год равна:
Второй подход заключается в учете возможного будущего вероятностного распределения доходности актива. Ожидаемая доходность актива в этом случае определяется как среднеарифметическая взвешенная, где весами выступают вероятности каждого события. В сумме все возможные варианты событий должный составлять 100%. Формулу ожидаемой доходности в этом случае: где r — ожидаемая доходность актива для i-го события, p — вероятность наступления i-го события.
Пример. Инвестор полагает, что в будущем году можно ожидать следующего вероятностного распределения доходности акции.
Ожидаемая доходность бумаги равна:
Портфель, формируемый инвестором, состоит из нескольких ценных бумаг, каждая из которых обладает своей ожидаемой доходностью. Ожидаемая доходность портфеля определяется как средневзвешенная ожидаемая доходность входящих в него бумаг: где Dр — ожидаемая доходность портфеля, r — ожидаемая доходность ценных бумаг, d — удельный вес в портфеле соответствующей ценной бумаги. Удельный вес ценной бумаги в портфеле рассчитывается как отношение ее стоимости к стоимости всего портфеля.
Пример. Портфель состоит из двух бумаг А и В. Стоимоть бумаги А составляет 300 руб., В — 700 руб. Определим ожидаемую доходность портфеля.
Стоимость портфеля равна
Удельные веса бумаг в портфеле составляют:
Ожидаемая доходность портфеля равна:
Таким образом, если инвестор объединяет в портфеле две бумаги, то значение ожидаемой доходности портфеля будет располагается между значениями ожидаемых доходностей первой и второй бумаг.
Содержание рассылки зависит и чем активнее Вы проявляете свою заинтересованность или иной теме, задаете те или иные вопросы — тем полезнее рассылка будет Пишите
Источник
Ожидаемая доходность
Из Википедии — свободной энциклопедии
Ожидаемая доходность — средневзвешенный, наиболее ожидаемый доход финансового инструмента. Показатель ожидаемой доходности учитывает все возможные доходы и определяет весомость того дохода, получение которого имеет наибольшую вероятность. В основу ожидаемой доходности положено понятие математического ожидания.
Ожидаемая доходность вычисляется по формуле:
M ( R ) = ∑ i = 1 n P i ∗ R i <\displaystyle \operatorname 
P i <\displaystyle P_> 

Например, если известно, что инвестиция даёт 50 % вероятности получения 10 % доходности, 25 % вероятности получения 20 % доходности, 25 % вероятности получения −10 % доходности, ожидаемая доходность будет равна 7,5 %
= (0,5) (0,1) + (0,25) (0,2) + (0,25) (-0,1) = 0,075 = 7,5 %
Фактическая доходность может отличаться от полученного значения ожидаемой доходности. Статистический метод вычисления дисперсии случайной величины позволяет измерить вероятность отклонения фактической доходности от ожидаемой доходности. Чем выше дисперсия доходности у финансового инструмента, тем больше неопределённость у инвестора о будущих доходах. Следовательно инструмент с большей величиной дисперсии доходности является более рискованным финансовым инструментом.
Источник
Показатели, используемые для оценки доходности и риска



| Показатель | Формула |
| Средняя ожидаемая доходность актива | 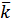 = = 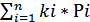 |
| Дисперсия актива | σ² = 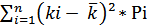 |
| Стандартное отклонение актива | σ = 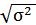 |
| Коэффициент вариации | 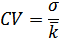 |
| Средняя ожидаемая доходность портфеля | 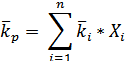 |
| Дисперсия портфеля | σp 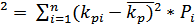 |
| Стандартное отклонение портфеля | σp = 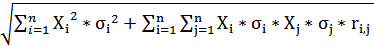 i≠j i≠j |
| Коэффициент корреляции для портфеля, состоящего из двух активов А и В | r = 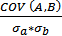 |
| Ковариация для портфеля, состоящего из двух активов А и B | COV= 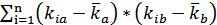 * * 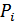 |
| Бета коэффициент ценной бумаги | 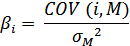 |
| Бета коэффициент портфеля | βр = 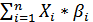 |
| Требуемая доходность эффективного портфеля (модель САРМ) | 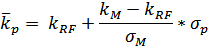 |
| Требуемая доходность ценной бумаги (модель САРМ) | 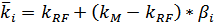 |
| Коэффициент эффективности У.Шарпа | SD = 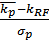 |
| Коэффициент риска | Kp = 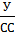 |
| Размах вариации | R = kmax-kmin |
Задачи
1. Имеется следующая оценка совместного вероятностного распределения доходностей от инвестиций в акции компаний А и Б:
| Общеэкономическая ситуация | Доходность А, % | Доходность Б, % | Вероятность |
| Спад | — 10 | 0,15 | |
| Без изменения | 0,20 | ||
| Незначительный подъем | 0,30 | ||
| Существенное оживление | 0,35 |
Вычислите ковариацию и коэффициент корреляции двух инвестиций.
Определим среднюю доходность акций:
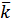
Для акции А: 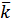
Для акции Б: 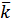
σ² =
Для акции А: σ² = (-10-9,5)²*0,15 + (5-9,5)²*0,2 + (10-9,5)²*0,3 + (20-9,5)²*0,35 = 99,75%
Для акции Б: σ² = (15-5,75)²*0,15 + (10-5,75)²*0,2 + (5-5,75)²*0,3 + (0-5,75)²*0,35 = 28,19%
Определим стандартное отклонение:
σ =
Для акции А: σ =
Для акции Б: σ = 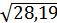
COV=
COV=(-10-9,5)*(15-5,75)*0,15 + (5-9,5)*(10-5,75)*0,2 + (10-9,5)*(5-5,75)*0,3 + (20-9,5)*(0-5,75)*0,35 = -52,125%
Определим значение коэффициента корреляции:
r =
Доходности двух инвестиций движутся в противоположных направлениях.
2. Ожидаемая доходность акций А и Б равна соответственно 12 и 25 %. Их среднеквадратическое отклонение равно 5 и 8%. Коэффициент корреляции между доходностями акций равен 0,6. Рассчитайте ожидаемую доходность и стандартное отклонение портфеля, состоящего на 40% из акций А и на 60% из акций Б. Определите ожидаемую доходность и стандартное отклонение портфеля, состоящего на 60% из акций А и на 40% из акций Б. Сравните полученные результаты.
Определим ожидаемую доходность портфеля, если 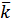
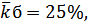
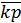
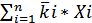
Рассчитаем стандартное отклонение портфеля, если σа = 5%, σб = 8%, rаб = 0,6:
σp = 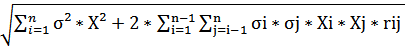
Определим те же показатели, но при другой структуре портфеля: Ха=0,6, Хб = 0,4
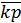
σp = 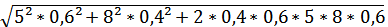
Первый портфель имеет более высокие показатели доходности и риска.
3. Инвестор владеет тремя видами акций. Он произвел оценку следующего совместного вероятностного распределения доходностей:
| Общеэкономическая ситуация | Вероятность | Доходность акции А | Доходность акции В | Доходность акции С |
| Спад | 0,30 | -10 | ||
| Без изменения | 0,20 | |||
| Незначительный подъем | 0,30 | |||
| Существенное оживление | 0,20 | -10 |
Определите ожидаемую доходность и стандартное отклонение портфеля, если инвестор вкладывает 30% средств в акции А, 50% — в акции В, 20% — в акции С. Предполагается, то доходность каждой ценной бумаги является некоррелированной с доходностью остальных ценных бумаг.
Для решения задачи необходимо определить
а) среднюю доходность по акциям А,В,С,
б) дисперсию для этих бумаг,
в) доходность и стандартное отклонение портфеля.
Определим среднюю доходность акций:
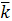
Для акции А: 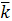
Для акции В: 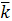
Для акции С: 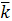
σ² =
σ² = (-10-4)²*0,3 + (0-4)²*0,2 + (10-4)²*0,3 + (20-4)²*0,2 = 124%
σ² = (10-4,4)²*0,3 + (8-4,4)²*0,2 + (6-4,4)²*0,3 + (-10-4,4)²*0,2 = 52,37%
σ² = (0-8,6)*0,3 + (10-8,6)*0,2 + (12-8,6)*0,3 + (15-8,6)*0,2 = 34,24%
Рассчитаем ожидаемую доходность портфеля при условии, что
Xа = 0,3, Xв = 0,5, Xс = 0,2:

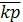
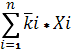
Рассчитаем стандартное отклонение портфеля:
σp =
Поскольку rij = 0, то
σp = 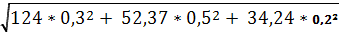
Следовательно, ожидаемая доходность портфеля составит 5,12%, а его стандартное отклонение 5,06%.
4.Портфель инвестора состоит из ценных бумаг со следующими характеристиками:
| Актив | Общая рыночная стоимость, руб. | Бета |
| А | 20 000 | 0,05 |
| Б | 4 000 | 0,90 |
| С | 5 000 | 1,10 |
| Д | 9 000 | 1,20 |
| Е | 2 000 | 1,80 |
Доходность безрисковых ценных бумаг равна 5%, доходность на рынке в среднем 10%. Определите бета портфеля, доходность портфеля.
Определим долю каждого актива в портфеле:
Ха =
Хб=
Хс=
Хд =
Хе =
βр = 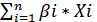
Рассчитаем nht,etve. доходность портфеля
Бета- коэффициент портфеля составит 0,59, а его ожидаемая доходность – 7,95%.
5. Пусть в портфель входят две ценные бумаги со следующими характеристиками:
| Ценная бумага | Ожидаемая доходность, % | Стандартное отклонение, % | Доля в рыночном портфеле |
| А | 0,40 | ||
| В | 0,60 |
При условии, что коэффициент корреляции этих ценных бумаг составляет 0,30, а безрисковая ставка равна 5%, определите уравнение рыночной линии.
Определим стандартное отклонение портфеля, если Ха = 0,4, Хб = 0,6, σа = 20%, σб = 28%, r = 0,3:
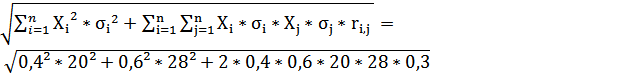
Рассчитаем среднюю доходность рыночного портфеля:
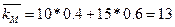
Определим уравнение рыночной линии:
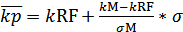
6. Компании А и Б планируют вложить денежные средства в ценные бумаги. При этом у А собственные средства составляют 70 млн.руб., а сумма возможного убытка в случае неправильного выбора объекта инвестирования может составить 1,2 млн.руб., у компании Б- 92 млн.руб., и 8 млн. руб. соответственно. Определите, какое из предприятий осуществляет менее рискованное вложение средств.
Для расчета воспользуемся коэффициентом риска:
Kp=
Коэффициент риска для компании А: Kp=
Коэффициент риска для компании Б: Kp=
Поскольку коэффициент риска у компании Б выше, то можно сделать вывод о более рискованном вложении средств со стороны этой компании.
7. По модели САРМ определите требуемую доходность акции, если:
— безрисковая ставка доходности составляет 8% годовых,
— среднерыночная ставка доходности финансовых активов – 15%,
— бета — коэффициент составляет 2.5.
Воспользуемся уравнением рыночной линии ценной бумаги:
Источник