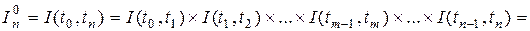Статический метод расчета периода окупаемости инвестиций
Еще до концепции дисконтирования денежных поступлений и затрат (начало 90-х годов девятнадцатого столетия), которая приобрела всеобщее признание в качестве способа получения самой точной оценки приемлемости инвестиций, аналитики инвестиционных проектов использовали в своем арсенале традиционные статистические методы; такие как методы расчета периода окупаемости инвестиций, метод определения бухгалтерской рентабельности инвестиций и ряд других.
Однако и по сей день эти методы остаются в арсенале разработчиков и аналитиков инвестиционных проектов. Причиной тому — возможность получения с помощью такого рода методов некоторой дополнительной информации, что является источником при оценке инвестиционных проектов, так как позволяет снижать примеры неудачного вложения денежных средств. И это характерно для предприятий малого бизнеса, ибо предпринимателю, не обладающему большим денежным капиталом, очень важно как можно быстрее вернуть внесенные в дело средства. Рассмотрим один из этих методов оценки инвестиционных проектов — статический метод расчета периода окупаемости инвестиций (РР-метод, англ. — Playback Period).
Данный метод позволяет определить тот срок, который понадобится для возмещения суммы первоначальных инвестиций. В качестве периода окупаемости капитала в данном случае рассматривается период, в течение которого суммарные расходы, связанные с осуществлением инвестиционного проекта, становятся равными суммарным получаемым доходам. Если величины денежных поступлений примерно равны по годам, то формула расчета периода по формуле расчета периода окупаемости имеет вид:
где РР — период окупаемости (лет); р — первоначальные инвестиции; Ft — среднегодовая сумма денежных поступлений от реализации инвестиционного проекта.
П р и м е р 8.2. Предприниматель вкладывает в реализацию проекта 1000 млн руб.
Здесь/0 = 1000; Ft= 250.
Тогда по формуле (8.3.1) определим срок окупаемости вложенных денежных средств, который составит
Если поток доходов неравномерный, то для расчета показателя РР используют так называемый кумулятивный метод, или метод накапливания, когда в процессе последовательного определения расходов и доходов по проекту и определяется период, в котором суммарные доходы становятся равными суммарным расходам. Чтобы лучше понять это, вновь обратимся к примеру 8.2.
П р и м е р 8.3. Возьмем тот же инвестиционный проект, что мы рассматривали в примере 8.2., но предположим, что денежные расходы и доходы по нему существенно различаются, нарастая со временем. Данные приведены в табл. 8.1.
Исходные данные по проекту
| Денеж потоки | Годы | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Расходы | 450 | 350 | 200 | — | — | — | — | — |
| Доходы | — | — | — | 100 | 150 | 300 | 450 | 500 |
Аналитический расчет показателя срока окупаемости можно определить по следующей формуле:
где 4 — инвестиционные вложения в проект в к-м временном интервале; Fk — доход предпринимателя от эксплуатации проекта в к-м временном интервале; п — инвестиционный цикл (лет); t- количество временных интервалов функционирования проекта, за которое суммарные инвестиции сравниваются с суммами доходов от эксплуатации проекта (это и будет искомый срок окупаемости).
Тогда расчет периода окупаемости будет предполагать пошаговые (с шагом в год или иной расчетный период, принятый для анализа данного проекта инвестиции) суммирования годичных сумм денежных поступлений до тех пор, пока результат не станет равным сумме инвестиций.
Так, в нашем примере нетрудно подсчитать, что период окупаемости инвестиций составляет 4 года, так как именно за этот период (начиная с 3 года по 6-й включительно) денежные поступления (100+150+300+450) достигнут величины суммарных инвестиционных вложений в 1000 млн руб.
Если период окупаемости рассчитывается на основе нарастающей суммы денежных поступлений, то может возникнуть ситуация, когда срок накопления суммы, равной первоначальным инвестициям, не кратен цело-
му числу лет (как удачно получилось в приведенном выше примере). Как определить длительность периода окупаемости в этом случае ?
П р и м е р 8.4. Допустим, например, что в том же рассматриваемом нами выше примере 8.3., денежные поступления по годам сложатся по- другому (табл. 8.2.)
Исходные данные к проекту
| Денежные Годы | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Расходы | 450 | 350 | 200 | — | — | — | — | — | — |
| Доходы | — | — | — | 100 | 120 | 280 | 350 | 300 | 300 |
Легко подсчитать, что в этом случае кумулятивная сумма денежных поступлений за 6 лет (850) меньше величины инвестиций (1000), а за 7 лет — (1100), что несколько больше.
Так в нашем примере 150 млн руб. составляют 0,5 суммы денежных поступлений на 7-м году реализации инвестиционного проекта (300 млн руб.), и, следовательно, общий срок окупаемости будет составлять шесть с половиной лет.
Суть производимых расчетов данного показателя может быть проиллюстрирована с помощью графика, представленного на рис. 8.2.
Рис. 8.2. График определения срока окупаемости инвестиций
Здесь по горизонтали оси откладывается текущее время в принятых временных интервалах (например в годах, полугодиях, кварталах, месяцах и т.д.). По вертикальной оси нарастающим итогом и в принятой валюте откладываются инвестиционные вложения и получаемые доходы. В результате образуются две кривые, которые в какой-то момент пересекаются. Координата рр на оси t точки Р пересечения этих кривых во времени и будет определять срок окупаемости инвестиций.
На рис 8.2. этот показатель составляет 6,5 лет. В рассмотренном примере суммарные вложения, как следует из графика, точно сравняются с суммой доходов от эксплуатации проекта через 6,5 лет, что полностью соответствует условию формулы (8.3.2)
Источник
Метод срока окупаемости
Различают два метода определения срока окупаемости:
1) Статический метод определения показателя срока окупаемости без учета фактора времени (неравноценности разновременных затрат и доходов). Показатель, рассчитанный этим методом, часто называют простым (недисконтированным) сроком окупаемости инвестиций.
2) Динамический метод определения показателя срока окупаемости с учетом дисконтирования доходов.
Несмотря на широкое распространение в аналитической практике, срок окупаемости следует использовать при оценке эффективности проектов, как правило, только в качестве ограничения. Срок окупаемости позволяет больше судить о ликвидности (особенно в условиях инфляции), чем об эффективности проекта, т.к. он не учитывает доходы, генерируемые проектом за пределами окупаемости.
Простой срок окупаемости равен минимальному числу интервалов времени (в месяцах или годах), по истечении которых сумма инвестиций покрывается (погашается) доходами от операционной и инвестиционной деятельности. В течение срока окупаемости чистый доход проекта становится, а в дальнейшем остается неотрицательным.
при котором 
, (11.24)
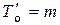
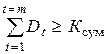
где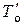 
– простой срок окупаемости инвестиций, мес. (лет);
m – число интервалов, мес. (лет), причем m ≤ n;
n – срок действия проекта, мес. (лет);
Ксум – суммарная величина инвестиций, руб.
Срок окупаемости в общем случае исчисляется либо от начала осуществления инвестиций, либо от момента ввода объекта в эксплуатацию.
Если поток доходов от операционной деятельности является постоянным, то простой срок окупаемости можно рассчитать делением суммы исходных капиталовложений на величину годового дохода, генерируемого проектом.
, (11.25)
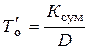
где 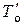– простой срок окупаемости, лет;
Ксум – суммарная величина исходных инвестиций, руб.;
D – годовой (или среднегодовой) доход, руб.
Срок окупаемости проекта с учетом дисконтирования доходов равняется минимальной продолжительности времени (минимальному числу интервалов), по истечении которой приведенные исходные инвестиции покрываются накопленным дисконтированным доходом, рассчитанным нарастающим итогом. Иными словами, в течение срока окупаемости с учетом дисконтирования показатель ЧДД, рассчитанный кумулятивным способом, становится положительным и в дальнейшем остается также положительным.
, при котором 
, (11.26)
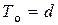
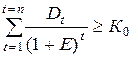
где То – дисконтный срок окупаемости инвестиций, мес. (лет);
d – число интервалов, мес. (лет), причем d ≤ n;
n – срок действия проекта, мес. (лет);
К0 – сумма приведенных исходных инвестиций, руб.
Критерием инвестиционной привлекательности отдельного проекта по сроку окупаемости является не превышение его нормативной величины, принятой инвестором:
, (11.27)
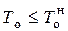
где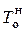 
– нормативный срок окупаемости инвестиций.
Простой срок окупаемости является “понятным”, элементарно рассчитывается и в силу этого широко используется практиками. Однако он имеет ряд недостатков, из-за которых становится некорректным инструментом даже для предварительной отбраковки альтернативных проектов. Во-первых, поскольку он основан на недисконтированных оценках, не делает различия между проектами с равной суммой кумулятивных доходов, но имеющих различное распределение доходов по годам (следовательно, отличающихся уровнем ЧДД). Во-вторых, не делает различия между проектами с различным сроком действия, поскольку не реагирует на доходы последних интервалов (лет) в течение срока действия проекта.
Дисконтный срок окупаемости, лишенный этих недостатков, может использоваться как критерий для предварительной отбраковки альтернативных проектов и как ограничение при принятии окончательного решения по отбору оптимального ИП.
Предприятие рассматривает целесообразность осуществления одного из четырех альтернативных проектов A, B, C и D. Барьерный уровень доходности составляет 10 %, нормативный срок окупаемости – 4 года. Необходимо проверить возможность принятия инвестиционного решения, используя показатели срока окупаемости 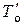и То.
Все проекты по простому сроку окупаемости приемлемы, причем А, В, Симеют одинаковый срок окупаемости. Проекты А и В имеют одинаковую сумму доходов за срок действия объекта DΣ = 15. Однако структура распределения этой суммы по первым трем годам неодинакова. У проекта А доходы нарастают постепенно, затем снижаются, а проект В генерирует понижающиеся доходы. Поэтому по дисконтному сроку окупаемости проект А уступает проекту В.
| Годы (t) | Коэффициент дисконтирования М2(10;t) | Проект А | Проект В | Проект С | Проект D | |||
| Денежный поток | Kt×M2(10;t); Dt×M2(10;t) | Денежный поток | Kt×M2(10;t); Dt×M2(10;t) | Денежный поток | Kt×M2(10;t); Dt×M2(10;t) | Денежный поток | Kt×M2(10;t); Dt×M2(10;t) | |
| 1,000 | –10 | –10 | –10 | –10 | –10 | –10 | –10 | –10 |
| 0,909 | 1,82 | 4,55 | 1,82 | 4,55 | ||||
| 0,826 | 2,48 | 2,48 | 2,48 | 4,13 | ||||
| 0,751 | 3,76 | 1,50 | 3,76 | 2,25 | ||||
| 0,683 | 2,05 | 2,05 | 3,42 | 2,05 | ||||
| 0,621 | 1,24 | 1,24 | 3,11 | 1,24 | ||||
 | – | – | – | – | – | |||
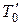| Т0 | – | – | – | 3,7 | – | 3,6 | – | 2,9 |
| DΣ | – | – | – | – | – | |||
| ЧДД | – | 1,35 | 1,82 | 4,59 | 4,17 |
Проект С дает максимальные постоянные доходы, начиная с 3-го года эксплуатации. В связи с этим он имеет по сравнению с проектом В лучшее значение дисконтного срока окупаемости (3,6 года), несмотря на одинаковый с ним простой срок окупаемости и невыгодную структуру распределения доходов в этот период. Проект D имеет лучшие показатели простого и дисконтного срока окупаемости по сравнению с проектом С, однако несмотря на это по показателю чистого дисконтированного дохода уступает проекту С. Из рассматриваемых альтернативных проектов оптимальным по максимальному значению ЧДД является проект С.
Тема 12. Учет влияния инфляции на эффективность ИП 
Оценка инфляции
При оценке эффективности капитальных вложений и выборе ИП необходимо учитывать влияние инфляции, поскольку она изменяет реальную стоимость поступлений и затрат, причем чаще всего не в равной степени (пропорции). Это отражается на величине рассчитываемых показателей эффективности инвестиций, ведет к их искажению.
Повышение цены на некоторый товар А характеризуется индексом цены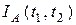 
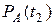
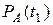
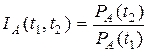
, который показывает отношение цены 
на этот товар в момент t2 к его цене 
в момент t1 :
. (12.1)
Индекс цены товара отражает изменение цены за весь рассматриваемый период t2 – t1. Если индекс цены рассчитан относительно некоторого начального (базового) для рассматриваемого случая момента времени, то такой индекс цены называется базисным.
, (12.2)
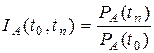
где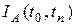 
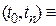
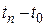
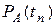
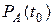
– базисный индекс цены товара А за период времени 
;
– цена товара А в момент tn;; 
– цена товара А в момент t0 ;
n – число шагов, на которые поделен рассматриваемый период времени.
Индекс цены обладает свойством:
, (12.3)
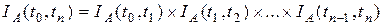
где 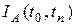– базисный индекс цены товара А;
n – число шагов в рассматриваемом периоде времени;
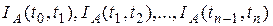
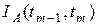
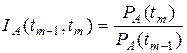
– цепные индексы цены товара А за соответствующий t1, t2, …, tn-й шаг.
Цепной индекс 
за некоторый tm-й шаг:
. (12.4)
Темп прироста (уменьшения) цены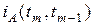 
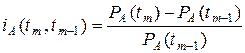
товара А за tm-й шаг определяется по формуле
. (12.5)
Под инфляцией понимают повышение общего (среднего) уровня цен на товары с течением времени.
Для оценки общей инфляции используют два основных показателя:
1) темп (уровень) инфляции,
2) индекс инфляции.
Темп инфляции (i) характеризует темп прироста среднего уровня цен на товары в рассматриваемом периоде (t2 – t1):
, (12.6)
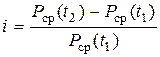
Индекс инфляции характеризует темп роста (изменения) средних цен в рассматриваемом периоде (t2 – t1):
. (12.7)
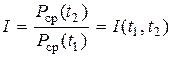
Базисный индекс общей инфляции:
. (12.8)
, (12.9)
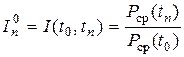
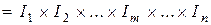
где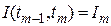 
– цепной индекс общей инфляции за некоторый tm-й (или m-й) шаг, отражающий отношение среднего уровня цен в конце и начале tm-го шага.
Темп общей инфляции:
. (12.10)
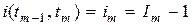
Темп инфляции в общем случае меняется с течением времени. Однако в расчетах часто делается допущение о равномерности инфляции, т.е. принимается i1 = i2 = . = im = . = in. Инфляция, темп которой не меняется с течением времени, называется равномерной (постоянной).
Цены на различные товары повышаются по-разному, их индексы цен отличаются друг от друга (следовательно, и от индекса общей инфляции). В этом случае инфляцию называют неоднородной. Если индексы цен различных товаров и индекс общей инфляции в рассматриваемый период времени совпадают, то инфляция является однородной.
Неоднородность инфляции по продукту А в период (t0, tn) определяется коэффициентом неоднородности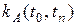 
:
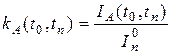
, (12.11)
где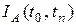 
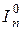
– базисный индекс цены продукта А за рассматриваемый период (t0, tn); 
– базисный индекс общей инфляции за тот же период.
Для однородной инфляции имеем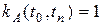 
.
Виды цен, используемые для задания ДП ИП
Для определения ДП и оценки эффективности ИП в связи с инфляцией различают и используют следующие виды цен:
— дефлированная (расчетная) цена.
Базисная (базовая) цена – это фиксированная цена, равная цене на момент разработки инвестиционного проекта или цене нулевого момента.
Прогнозная (номинальная) цена представляет собой ожидаемую цену в будущем, иначе реальную цену конкретного продукта (ресурса), действующую на определенный момент времени. Для устранения влияния инфляции необходимо привести эти элементы ДП к единой покупательной способности, т.е. дефлировать ДП.
Установление прогнозной цены осуществляется расчетным путем на основе экспертной оценки индекса цены конкретного продукта по формуле
, (12.12)
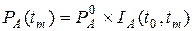
где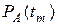 
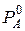
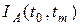
– прогнозная цена продукта (элемента) А в конце m-го шага;
–базисная цена продукта (элемента) А;
– базисный индекс цены продукта А в конце m-го шага.
Дефлированная цена рассчитывается по формуле
, (12.13)
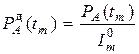
где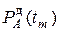 
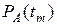
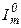
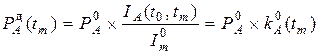
и 
– дефлированная и прогнозная цена продукта А на шаге m ;
– базисный индекс общей инфляции.
, (9.14)
где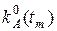 
– коэффициент неоднородности инфляции по продукту А.
Дефлированная цена зависит не столько от самой инфляции (индекса общей инфляции), сколько от коэффициента неоднородности инфляции. Если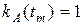 
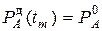
, т.е. инфляция однородна, имеем 
. Это означает, что в этом частном случае расчет показателей эффективности можно вести по ДП, выраженному в базисных ценах.
Учет влияния инфляции на эффективность ИП
Учет влияния инфляции на эффективность ИП, ДП которого выражен в прогнозных ценах, можно устранить двумя способами:
1) корректировкой ставки дисконта по формуле Фишера, при этом номинальная ставка используется для расчета показателей эффективности, определяемых дисконтированием ДП;
2) дефлированием денежного потока, который используется для расчета всех необходимых для оценки эффективности ИП показателей, определяемых без дисконтирования и дисконтированием по реальной ставке дисконта.
Соотношения между номинальной и реальной ставками дисконта
Пример 12.1Инвестор готов осуществить инвестицию в 1 тыс.руб., исходя из доходности 20% годовых, т.е. рассчитывая получить через год доход (1 + 0,20) = 1,20 тыс.руб. Если уровень инфляции составляет 20 % в год, то, чтобы сохранить желаемую покупательную способность дохода, получаемое через год денежное поступление должно быть больше на величину индекса инфляции, т.е. должно составлять:
1 ´ (1 + 0,2) ´ (1 + 0,15) = 1,38 тыс.руб.
Отсюда следует, что в условиях инфляции в операциях наращения и дисконтирования следует пользоваться не 20 %-й ставкой доходности, а скорректированной– 38 %.
Поэтому в условиях инфляции различают реальную ставку дисконта (доходности) и номинальную ставку дисконта.
Реальная ставка дисконта – это дисконтная ставка в постоянных (фиксированных) ценах, не учитывающая инфляцию, последующую от момента рассмотрения (нулевого момента).
Номинальная ставка дисконта – это ставка дисконта, скорректированная на уровень инфляции в прогнозируемом периоде, величина которой обеспечивает доходность инвестиций на уровне реальной ставки дисконта.
Связь между номинальной и реальной ставками дисконта определяется формулой Фишера:
, (12.15)
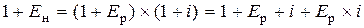
где Ен – номинальная ставка дисконта, применяемая в условиях инфляции;
Ер – реальная ставка дисконта;
i – темп инфляции в долях единицы в единицу времени (год, месяц) или, что то же самое, за шаг расчета. При небольших значениях Ер и i, произведение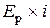 
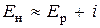
может стать пренебрежимо малой величиной. Тогда можно принять 
.
Устранение влияния равномерной инфляции корректировкой ставки дисконта (пример)
Пример 12.2 Необходимо определить экономическую целесообразность проекта, характеризующегося денежным потоком: –130; 60; 60; 60; 60, заданным в прогнозных ценах (тыс.руб.), если приемлемая норма доходности – 24 % годовых, среднегодовой темп инфляции – 9 %.
Источник