Стандартное отклонение коэффициент корреляции между доходностями активов

Коэффициент корреляции | Correlation coefficient

В статистике коэффициент корреляции (англ. Correlation Coefficient) используется для проверки гипотезы о существовании зависимости между двумя случайными величинами, а также позволяет оценить ее силу. В портфельной теории этот показатель, как правило, используется для определения характера и силы зависимости между доходностью ценной бумаги (актива) и доходностью портфеля. Если распределение этих переменных является нормальным или близким к нормальному, то следует использовать коэффициент корреляции Пирсона, который рассчитывается по следующей формуле:

— среднеквадратическое (стандартное) отклонение доходности i-ой ценной бумаги;

— среднеквадратическое (стандартное) отклонение доходности портфеля.

В расширенном виде формулу коэффициента корреляции Пирсона можно записать следующим образом:

где k_i – доходность ценной бумаги в i-ом периоде;

— ожидаемая (средняя) доходность ценной бумаги;

p_i – доходность портфеля в i-ом периоде;

— ожидаемая (средняя) доходность портфеля.

n – количество наблюдений.

Свойства коэффициента корреляции

Значение коэффициента корреляции изменяется от -1 до +1. Его отрицательное значение говорит о том, что между переменными наблюдается обратная взаимосвязь. Например, когда доходность ценной бумаги будет расти, то доходность портфеля будет падать, и наоборот. Положительное значение свидетельствует о прямой взаимосвязи, то есть, если доходность ценной бумаги будет расти, доходность портфеля также будет расти, и наоборот.

Если абсолютное значение коэффициента корреляции находится ближе к 1, то это свидетельствует о сильной взаимосвязи между переменными, а если ближе к 0 — то это говорит о слабой связи или ее отсутствии. Если его значение равно -1 или +1, то можно говорить о существовании функциональной взаимосвязи между переменными, то есть одну из них можно выразить через другую посредством математической функции.

Пример расчета

Динамика доходности акций Компании А и Компании Б, а также динамика доходности портфеля ценных бумаг выглядят следующим образом:

Чтобы использовать формулу коэффициента корреляции Пирсона необходимо рассчитать среднюю доходность, которая составит:

• для акций Компании А 4,986%;
• для акций Компании Б 5,031%;
• для портфеля 3,201%.

Ковариация доходности акций Компании А и портфеля составит -0,313, а акций Компании Б и портфеля 0,242. (О том, как рассчитывается ковариация доходности можно прочитать здесь)

Среднеквадратическое отклонение доходности акций Компании А составит 0,6398, акций Компании Б 0,5241 и портфеля 0,5668. (О том, как рассчитывается среднеквадратическое отклонение можно прочитать здесь)

Коэффициент корреляции доходности акций Компании А и доходности портфеля составит -0,864, а акций Компании Б 0,816.

R_Б = 0,242/(0,5241*0,5668) = 0,816

Можно сделать вывод о присутствии достаточно сильной взаимосвязи между доходностью портфеля и доходностью акций Компании А и Компании Б. При этом, доходность акций Компании А демонстрирует разнонаправленное движение с доходностью портфеля, а доходность акций Компании Б однонаправленное движение.

Источник

Задача №787 (расчет коэффициента корреляции доходностей активов)

Доходность двух активов за 8 периодов представлена в таблице:

Периоды	1	2	3	4	5	6	7	8
Доходность актива Х	10	14	10	8	-5	-3	3	7
Доходность актива У	14	18	13	10	-2	-7	-2	10

Определить коэффициент корреляции доходностей активов X и У.

Рекомендуемые задачи по дисциплине

Задача №109 (оценка риска изменения цены на продукцию)

Цены на металлопродукцию за последние 11 месяцев по статистическим данным составили: Месяц 1 2 3 4 5 6 Цена, долл./т 300 310 312 309 302 305 Месяц 7 8 9 10 11 Цена.

Задача №1576 (анализ рисков инвестиционных проектов)

Имеются два инвестиционных проекта: ИП1 и ИП2 с одинаковой прогнозной суммой требуемых капитальных вложений. Величина планируемого дохода (тыс.

Задача №2453 (оценка степени риска активов)

Вы располагаете следующими видами активов: ГКО, муниципальная облигация, привилегированная акция «Промстройбанка», обыкновенная акция.

Задача №834 (способы снижения рисков)

Заполнить таблицу: Виды риска Способы уменьшения отрицательных последствий 1) низкие объемы реализации товаров 2) неэффективная работа сбытовой сети 3) неудачный выход на.

Задача №787 (расчет коэффициента корреляции доходностей активов)

Доходность двух активов за 8 периодов представлена в таблице: Периоды 1 2 3 4 5 6 7 8 Доходность актива Х 10 14 10 8 -5 -3 3 7 Доходность актива У 14 18 13 10 -2 -7 -2 10 .

Обновить

Задачи

ПОДСКАЗКА!
Для заполнения
формы заказа
переходите по ссылке
Решение задачи
————>
Стоимость любой задачи —
50 руб.
Фрагменты решения
————>
Подробности и
ФОРМА ЗАКАЗА

Анализ финансового состояния российских компаний

Период анализа — 3 года
(например, 2018-2020 гг.)

Использована официальная отчетность компаний

Коэффициенты, таблицы,
рисунки, выводы.

Горизонтальный и вертикальный анализ баланса,
анализ ликвидности и платежеспособности,
анализ финансовой устойчивости,
анализ финансовых результатов и рентабельности,
анализ вероятности банкротства
и другие разделы
от 50 руб.

БЕСПЛАТНАЯ демонстрационная версия отчета

Предлагаем воспользоваться консультацией по решению задач, условия которых размещены на страницах сайта. Стоимость одной задачи — 50 рублей.

Все задачи УЖЕ решены. Под условием каждой задачи Вы можете увидеть ФРАГМЕНТЫ решения.

Файл с задачей высылается в формате Word и предполагает максимально подробные пояснения выполненных расчетов и полученных результатов.

Для получения подробной информации и заказа переходите по ссылке «Решение задачи», размещенной под условием каждой задачи.

С уважением, администратор сайта.

Предлагаем ознакомиться с информацией о выполненных работах по финансовому анализу российских компаний:

1. Каждая работа по финансовому анализу состоит из 10-ти разделов по банкам и 12-ти разделов по остальным компаниям..

2. Общий объем — от 80 до 120 страниц (методика, таблицы, рисунки, анализ всех показателей, выводы).

3. Стоимость любого раздела — 50 руб. или вся работа за 500 руб. У Вас есть возможность заказать только нужные Вам разделы работы.

4. Расчеты выполнены по самой последней опубликованной отчетности компании с официального сайта. Отчетность к работе прилагается.

5. Оплата производится только после ознакомления с демонстрационной версией работы.

6. Все интересующие Вас вопросы можно задать в переписке с автором работы.

Источник

Asset Allocation: корреляция активов

Автор: Алексей Мартынов · Опубликовано 23.05.2016 · Обновлено 22.08.2016

В предыдущей статье мы говорили, что ребалансировка активов контролирует риск портфеля, а при удачном стечении обстоятельств может дать дополнительный выигрыш по доходности. Но это работает только в том случае, если активы в портфеле ведут себя по разному в одних и тех же условиях. Как найти такие активы, и как оценить их поведение между собой, вы узнаете из этой статьи.

В портфель должны включаться слабо взаимосвязанные активы, цена которых ведет себя по разному в одинаковых условиях. Это снижает риск портфеля и создает портфельный эффект. Связь разных активов между собой можно оценить математически с помощью корреляции. Корреляция показывает в какой степени динамика стоимости одного актива соотносится с динамикой другого актива.

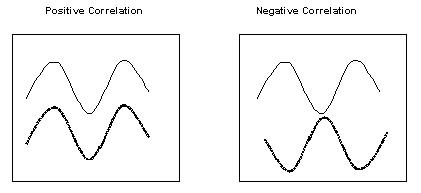
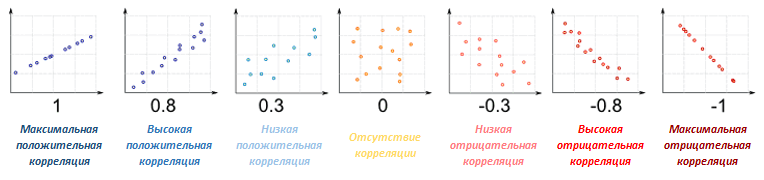
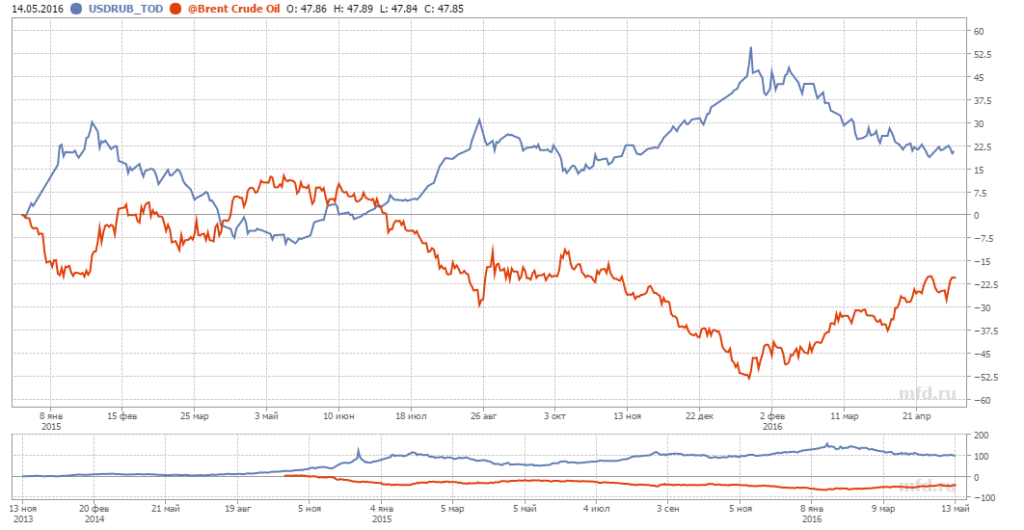
Корреляция может принимать значения от +1 (положительная) до -1 (отрицательная). Если цены активов движутся в одном направлении (оба растут или оба снижаются), корреляция положительна (больше 0), если цены активов движутся в противоположных направлениях (один растет, второй снижается), корреляция отрицательная (меньше 0). Корреляция равная +1 означает, что стоимость активов меняются идентично друг другу: если один актив вырос на 10%, второй тоже растет на 10%. Корреляция равная -1 означает, что цены движутся максимально противоположно. Нулевая корреляция означает, что взаимосвязи нет.

Из реальной жизни пример негативной корреляции можно найти в динамике курса доллара и цен на нефть в 2015-16 годах: когда нефть падала, курс доллара рос.

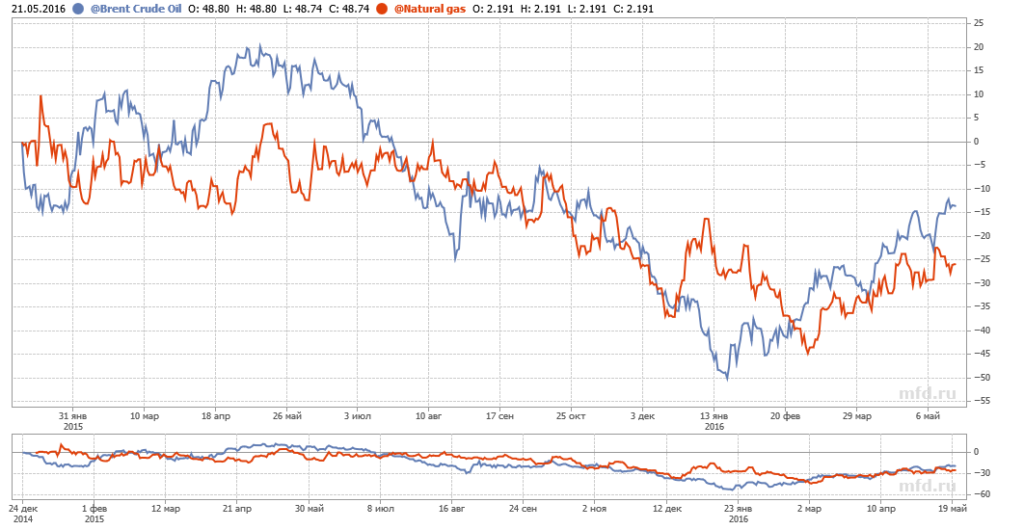
Положительная корреляция есть между ценами на нефть и натуральный газ: их цены двигаются схожим образом.

Влияние корреляции на риск портфеля

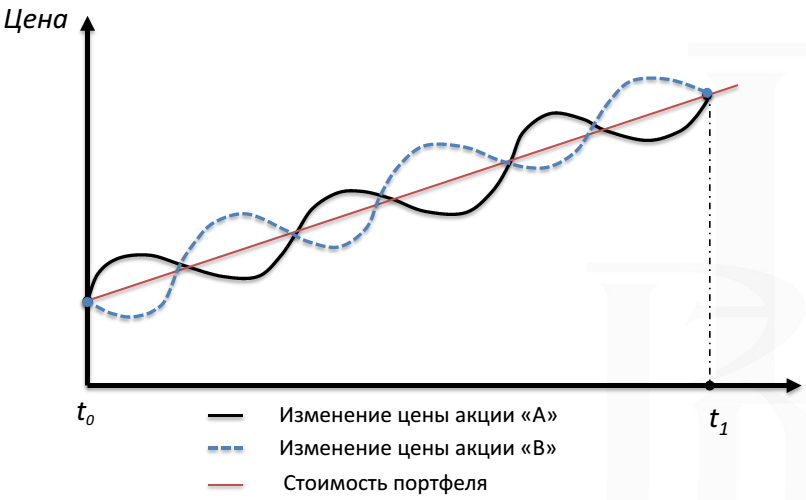
Поведение активов влияет на риск портфеля. Например, на картинке ниже изображены две акции, стоимость которых изменяется противоположно: когда одна растет, другая падает. Корреляция таких акций будет отрицательной. Если портфель будет состоять поровну их этих акций, то его стоимость будет изменяться гораздо плавнее по сравнению с каждой акцией в отдельности, то есть риск портфеля будет ниже, чем риск составляющих его акций. Это конечно идеализированная модель, но она наглядно показывает, как отрицательная корреляция активов снижает риск портфеля.

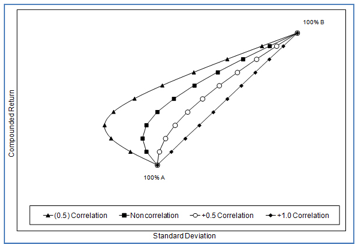
Теперь посмотрим, как корреляция может влиять на риск и доходность портфеля. На графике ниже изображена так называемая граница эффективности портфеля, состоящего из двух активов — А и В. Вертикальная ось — доходность портфеля, горизонтальная ось — стандартное отклонение доходности. Каждая линия представляет собой портфель с разной степенью корреляции активов (-0.5, 0.0, +0.5 и +1.0). Каждая точка на линии — это разные пропорции активов в портфеле, начиная от 100% А, далее 90% А:10% В и так далее до 100% В.

Источник: Richard Ferri, Portfolio Solutions

Нетрудно заметить, что портфели активов с отрицательной корреляцией -0,5 находятся в левой части диаграммы и имеют самое низкое стандартное отклонение доходности, то есть самый низкий риск среди всех рассматриваемых портфелей. А портфели активов с высокой корреляцией имеют самый высокий риск. Таким образом при прочих равных риск портфеля снижается когда активы имеют низкую корреляцию.

Корреляция активов

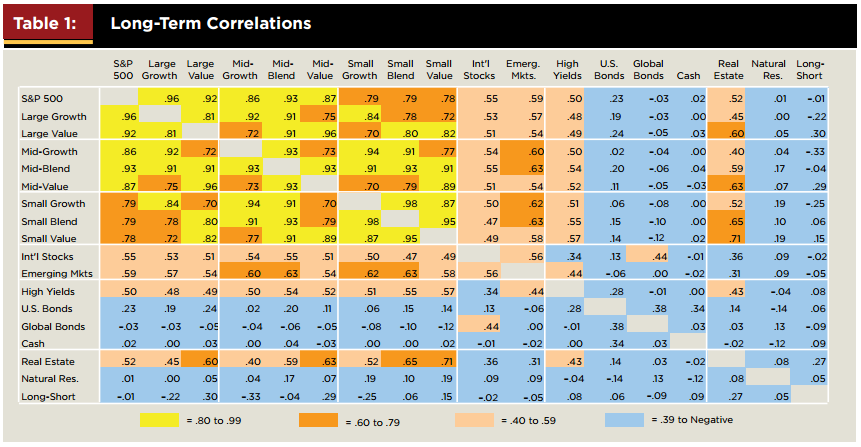
К сожалению, в реальной жизни довольно трудно найти два актива с абсолютно нулевой или отрицательной корреляцией. Большинство активов имеют корреляцию где-то между 0 и+1. В таблице 1 представлена матрица корреляции между разными классами активов с 1970 по 2004 год. Чем холоднее цвет, тем ниже корреляция. Можно заметить, что холодные цвета присутствуют в основном у облигаций, кэша и ресурсов. Эти классы активов хуже всего коррелируют с акциями различной капитализации и недвижимостью. Однако даже среди них редко встречаются отрицательные значения.

Источник: Journal of financial planning

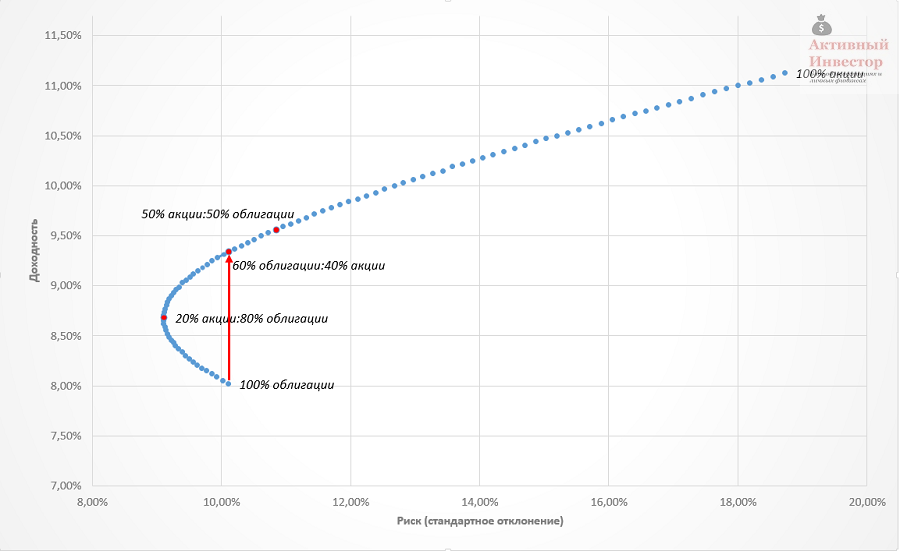
Если взять реальный пример, то корреляция между американскими акциями и долгосрочными государственными облигациями на сроке 1972-2015 составила 0,01, то есть фактически отсутствовала. Граница эффективности портфеля, состоящего их этих двух классов активов очень похожа на линию на графике выше, которая соответствует портфелю из некоррелируемых активов.

Низкая корреляция между активами создает портфельный эффект — когда по характеристикам риск и доходность портфеля может быть лучше активов, из которых он состоит. Логично было бы ожидать, что самый низкий риск будет иметь портфель, состоящий полностью из облигаций. Но в реальности самым низким риском обладает портфель, доля облигаций в котором 80%, а на акции приходится 20%. Добавление акций не только уменьшило риск портфеля, но и увеличило его доходность на 0,6%. Другой портфель 60:40 показал такой же риск, как и 100% облигаций, но его доходность при этом была почти на 1,5% больше.

Корреляция непостоянна

Ричард Ферри в своей статье в журнале Forbes обратил внимание, что, к сожалению, теория, которая красиво выглядит на длительном сроке, не всегда хорошо работает на коротких периодах. Например, с 1926 по 2013 год корреляция между акциями США и 5-летними казначейскими облигациями была равна 0,07. Это очень низкая корреляция для двух классов активов, значит эти два класса активов в портфеле должны хорошо работать вместе.

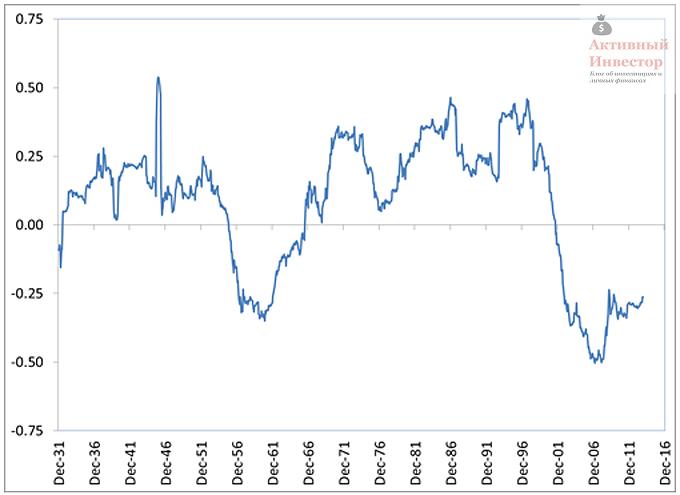
К сожалению, долговременная корреляция не отражает то, что происходит в течение коротких периодов. На графике ниже показано, как сильно может меняться корреляция на коротком сроке. На рисунке изображена 5-ти летняя скользящая корреляция между американскими акциями и 5-летними облигациями, рассчитанная на отрезке 1926-2013.

Источник: Richard Ferri, Portfolio Solutions

Пятилетняя корреляция колебалась в диапазоне от -0,5 до +0,5 и лишь изредка равнялась долгосрочной. Это означает, что какую-то часть времени стоимость активов менялась схожим образом, какую-то часть времени — противоположно. Корреляция активов не статична и меняется со временем, иногда очень сильно. Поэтому реализация преимущества низкой корреляции может потребовать длительного времени величиной с десятилетия.

Теперь возьмем и сравним поведение портфеля на двух временных промежутках: с 1970-1985 и с 2002-2013. В период с 1970-1985 корреляция между этими двумя классами активов составляла около +0,3, что привело к доходности портфеля 50:50 всего на 0,5% больше облигаций.
За период с 2002 по 2013 год корреляция между этими двумя классами активов составила около -0,3, в результате чего доходность портфеля превзошла доходность облигаций на 1,7%. Разная корреляция активов может очень сильно менять результаты одного и того же портфеля.

Источник: Richard Ferri, Portfolio Solutions

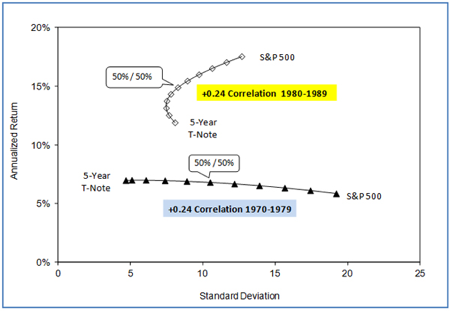
Но даже если корреляция в будущем будет такой же, как она была в прошлом, результаты все равно могут отличаться. Например, 10-летняя корреляция между 5-летними облигациями и акциями США в 70-х годах была +0,24, такой же она была и в 80-х. Но результаты портфелей были различными.

Источник: Richard Ferri, Portfolio Solutions

Низкая корреляция в 70-х годах не дала особых преимуществ: риск портфеля 50/50 оказался выше, а доходность ниже, чем у облигаций. В 80-х аналогичный портфель показал результат гораздо лучше: на 3% больше доходности облигаций при аналогичном риске. Поэтому низкая корреляция двух активов еще не гарантирует уменьшение риска портфеля на коротком сроке.

С течением времени активы с низкой корреляцией находить стало труднее. Финансовые рынки стали более глобальными и взаимосвязанными. Локальный ипотечный кризис 2008 года в США затронул весь мир. Глобализация финансовых рынков сделала так, что инструменты сейчас коррелируют в большей степени, чем раньше. Величина корреляции активов в прошлом зависит от взятого периода и не является надежным индикатором корреляции в будущем.

1. Активы, включаемые в портфель, должны иметь низкую положительную или отрицательную корреляцию.
2. Низкая корреляция снижает риск портфеля и может увеличить его доходность.
3. Долгосрочная корреляция в прошлом — плохой прогнозный индикатор будущей корреляции в краткосрочной перспективе.
4. Краткосрочная корреляция — величина непостоянная и может значительно меняться.
5. Поэтому для реализации преимущества низкой корреляции требуется длительное время.
6. На промежутках времени до 10 лет портфельный эффект может отсутствовать.

Тем не менее это вовсе не означает, что про корреляцию можно совсем забыть. В портфель нужно включать фундаментально разные активы. Высокая положительная корреляция означает отсутствие фундаментальных отличий по риску между активами. Например, высокая положительная корреляция между акциями крупной и средней капитализации будет всегда. Диверсификация по таким активам не принесет большой выгоды портфелю в плане снижения риска. Слабая положительная или отрицательная корреляция служит признаком отличий между активами в плане риска, поэтому включение в портфель активов с низкой положительной или отрицательной корреляцией потенциально уменьшает его риск и создает портфельный эффект, о котором будет написана следующая статья.

Источник