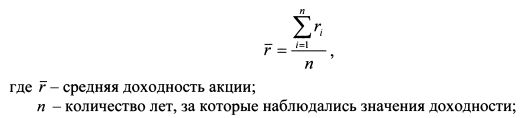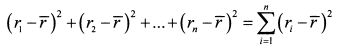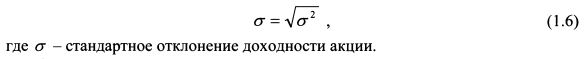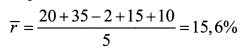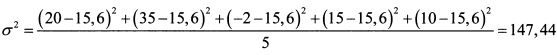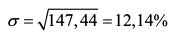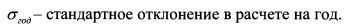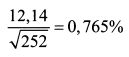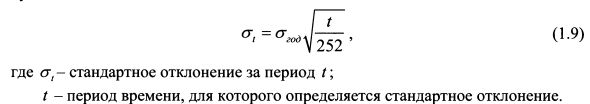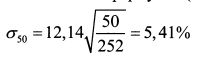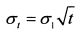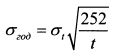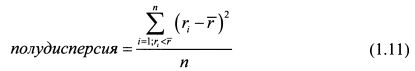Стандартное отклонение доходности от среднего значения

Стандартное отклонение

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

• в финансах в качестве меры волатильности,
• в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

• А -> (19 + 21 + 19+ 21) / 4 = 20
• Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

• в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
• в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

• стандартное отклонение компании A = 1,
• стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с «n–1»),
• полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

1. Вычесть среднее значение из каждого числа
2. Возвести каждый результат в квадрат (так получатся квадраты разностей)
3. Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

• одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
• двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
• трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

• при 20 % — выборка сильно вариабельна.

Источник

1.2. Ожидаемый риск портфеля. 1.2.1. Риск актива

Основополагающими мерами риска финансового актива являются такие показатели как стандартное отклонение и дисперсия его доходности. В качестве синонима понятия стандартное отклонение используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива говорят о степени возможного разброса его фактической доходности вокруг его средней доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива. Рассмотрим технику определения дисперсии и стандартного отклонения доходности на примере акции.

Пусть имеются значения доходности акции за п лет. За первый год она составила величину r1, за второй – r2, третий –r3 г3 и т.д., за п-й год – rn. Разобьем расчеты на несколько шагов.

ШАГ 1. Определяем среднее значение доходности акции за п лет. Это просто среднее арифметическое значений ее доходности за этот период:

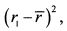
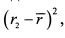
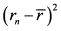
ШАГ 2. Определяем для каждого года отклонение фактического значения доходности от ее средней доходности, и возводим полученные данные в квадрат. Для первого года получаем: для второго года – и т. д., для n-го года – .

ШАГ 3. Суммируем квадраты отклонений:

ШАГ 4. Делим полученную сумму на количество лет:

Величина 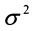является дисперсией доходности акции в расчете на год. Как уже отмечалось, дисперсия является показателем рассеяния фактических значений доходности акции вокруг ее средней доходности. Размерность дисперсии представляет собой квадрат доходности акции. Если в формуле мы учитываем доходность в процентах, то размерность дисперсии – это процент в квадрате. Показателем такой размерности не всегда удобно пользоваться, поскольку сама доходность акции измеряется в процентах. Поэтому из дисперсии извлекают квадратный корень и получают стандартное отклонение доходности:

Стандартное отклонение измеряется уже в процентах, т.е. в тех же единицах, что и сама доходность.

Если предположить, что при расчете дисперсии и стандартного отклонения мы учли все существующие значения доходности, т. е., как говорят, всю генеральную совокупность случайной переменной, то полученная по формуле (1.5) дисперсия называется генеральной дисперсией, а стандартное отклонение в формуле (1.6) – генеральным стандартным отклонением. Однако на практике невозможно учесть все фактические значения доходности акции, так как это непрерывная случайная величина. Поэтому оценку данных показателей проводят на основе только части их значений, т.е. на основе некоторой выборки данных. Тогда в результате расчета по формуле (1.5) получают так называемую выборочную дисперсию.

Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то она будет приводить к систематическим ошибкам, занижая значение генеральной дисперсии. Это происходит потому, что при расчете отклонения его считают не от истинного среднего значения переменной, а от выборочного. Выборочное же среднее непосредственно находится в центре выборки и поэтому отклонения от него выборочных данных в среднем меньше, чем от действительного среднего значения переменной в генеральной совокупности. Чтобы скорректировать данную погрешность переходят к так называемой исправленной дисперсии. Она определяется по формуле:

Формула (1.7) отличается от формулы (1.5) только знаменателем. Данная корректировка осуществляется для того, чтобы получить несмещенную оценку генеральной дисперсии. Корректировка является существенной, если оценку дисперсии проводят на основе небольшого количества данных. При большом объеме выборки различие в расчетах будет незначительным. На практике пользуются исправленной дисперсией, если количество наблюдений примерно меньше 30. Соответственно исправленное стандартное отклонение определяется по формуле:

Определить выборочное стандартное отклонение доходности акции, если ее доходность за первый год составила 20%, второй — 35% , третий — минус 2%, четвертый — 15% , пятый — 10%.

ШАГ 1. Определяем среднюю доходность акции:

ШАГ 2. Определяем дисперсию доходности согласно формуле (1.5):

ШАГ 3. Определяем выборочное стандартное отклонение доходности акции:

Рассматривая технику определения стандартного отклонения и цифровой пример, мы оперировали временным периодом равным году. На практике возникает задача определения стандартного отклонения для других временных периодов.

Если имеется значение стандартного отклонения за год, то для определения его за один день надо стандартное отклонение в расчете на год разделить на корень квадратный из количества торговых дней в году. В году насчитывается порядка 252 дней. Поэтому стандартное отклонение доходности актива за день получим по формуле:

Так, стандартное отклонение доходности акции за один день в приведенном выше примере равно:

Если мы определяем стандартное отклонение за некоторый период на основе годичного стандартного отклонения, то в общем виде формула имеет следующий вид:

Пусть в нашем примере требуется определить стандартное отклонение доходности акции за 50 дней. В соответствии с формулой (1.9) оно составляет:

Если известно стандартное отклонение за один день, то определить его в расчете на год можно по формуле:

Соответственно стандартное отклонение за любой другой период времени (ст,) определяется по формуле:

Получить стандартное отклонение за год на основе его значения за некоторый период t можно с помощью следующей формулы:

На практике волатильность часто определяют на основе данных о ежедневной доходности акции. Доходность акции за один день определяется по формуле:

Показатель rt является первым статистическим наблюдением. Далее берут цену акции при закрытии для дня t2 и определяют аналогичным образом доходность акции за второй день и т.д. На основе полученных данных о ежедневной доходности по формуле стандартного отклонения определяют волатильность в расчете на один день. Затем по формуле (1.10) определяют волатильность в расчете на год. Обычно в литературе показатель стандартного отклонения приводится в расчете на год, если не сказано иное.

Удобство расчета стандартного отклонения на основе ежедневных данных состоит в том, что можно воспользоваться большим количеством наблюдений. В то же время, при определении волатильности за год на основе значения волатильности за день можно допустить существенную погрешность. Она будет особенно велика, если стандартное отклонение актива следует процессу «mean reversion» (возвращение к среднему значению). «Mean reversion» означает, что волатильность актива в долгосрочной перспективе испытывает колебания вокруг некоторого среднего значения, а не возрастает бесконечно пропорционально величине \t .

На практике приемлемый результат получается, если рассчитывать стандартное отклонение для более длительных периодов на основе более коротких, используя период времени до 10 дней. Так, определив волатильность в расчете на день, можно рассчитать волатильность для десятидневного периода, умножив полученную цифру на V10 .

Когда инвестора интересует волатильность за более длительные периоды, можно взять прошлые статистические данные с требуемым интервалом. Например, инвестор определяет волатильность для одного месяца. Тогда необходимо взять наблюдения за предыдущие периоды времени по 30 дней. Причем, чтобы исключить автокорреляцию9, следует использовать не пересекающиеся временные периоды. Неудобство такого подхода при расчете волатильности для больших периодов состоит в том, что приходится использовать наблюдения за несколько предыдущих лет. При определении стандартного отклонения в расчете на месяц хорошую оценку риска можно получить, если учесть помесячные данные доходности за период времени не меньше трех лет.

Доходность актива является случайной величиной и поэтому может принимать различные значения. Если значения переменной изменяются во времени неопределенным образом, то говорят, что она следует стохастическому, т. е. вероятностному процессу. Значения переменной могут изменяться дискретно или непрерывно. В первом случае величина переменной изменяется только на определенную (дискретную) величину, во втором — может принимать любые значения в рамках некоторого диапазона.

Значения одной переменной могут изменяться только в определенные моменты времени, другой — в любое время. Поэтому выделяют соответственно дискретный и непрерывный стохастические процессы.

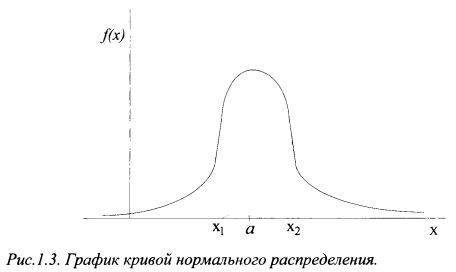
Доходность актива является непрерывной случайной величиной и подчиняется некоторому вероятностному распределению. Наиболее часто в жизни встречается нормальное распределение. Оно возникает в том случае, когда на случайную величину оказывает влияние множество факторов, каждый из которых не имеет определяющего значения. График кривой нормального распределения (его еще называют графиком плотности вероятности) случайной величины приведен на рис. 1.3. По оси абсцисс представлена область возможных значений случайной величины X, по оси ординат — плотность распределения вероятностей случайной величины X. В самом общем виде можно дать следующее определение плотности вероятности: это вероятность, приходящаяся на единицу длины отрезка, на котором может принимать значения случайная величина. Если быть более точным, то она характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке.

Плотность распределения f(x) является одной из форм закона распределения случайной величины, но существует только для непрерывных случайных величин.

График кривой нормального распределения симметричен относительно среднего значения случайной величины, которое называют еще математическим ожиданием случайной величины. На графике точка а является математическим ожиданием случайной величины X. Сама случайная величина может принимать любые отрицательные и положительные значения. Правая и левая ветви графика асимптотически приближаются к оси абсцисс. Вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Если нас интересует вероятность попадания случайной величины на какой-либо интервал оси абсцисс, то она будет равна площади фигуры, ограниченной сверху кривой распределения, снизу — осью абсцисс, по бокам — перпендикулярами, проходящими через концы интервала. Так, вероятность попадания случайной величины X на отрезок (х2х<) (см. рис. 1.3) равна площади фигуры, заштрихованной косыми пунктирными линиями. Нормальное распределение полностью определяется двумя характеристиками случайной величины - ее математическим ожиданием и стандартным отклонением. Таким образом, зная математическое ожидание и стандартное отклонение случайной величины, мы имеем полную картину вероятностного распределения ее возможных значений.

Стандартное отклонение характеризует степень рассеяния возможных значений случайной величины вокруг ее среднего значения. Кроме этого, оно говорит о вероятности того, что значение случайной переменной окажется в некотором интервале. Для нормально распределенной случайной величины полезно запомнить так называемое «правило трех сигм». Оно говорит о том, что вероятность получить значение случайной переменной в диапазоне одного стандартного отклонения от ее средней величины равно 68,3%, в диапазоне двух стандартных отклонений — 95,4%, трех стандартных отклонений — 99,7%. Остается еще 0,3% вероятности того, что случайная величина примет любое другое значение, выходящее за рамки отмеченных границ.

Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.

Проиллюстрируем данное правило на основе примера по расчету волатильности, который был приведен выше. Среднее значение, т.е. математическое ожидание доходности акции равнялось 15,6%, а стандартное отклонение доходности в расчете на год — 12,14%. Согласно правилу трех сигм, инвестор вправе ожидать, что с вероятностью 68,3% доходность акции через год будет располагаться в интервале от 15,6% ±12,14%, т.е. от 3,46% до 27,74%. С вероятностью 95,4% этот интервал составит 15,6%±2*12,14%, т.е. от -8,68% до 39,88%. С вероятностью 99,7% интервал возможной доходности будет равен 15,6% ±3*12,14% или от -20,82% до 52,02%. Остаются еще 0,3% вероятности того, что акция принесет как гораздо более высокую так и низкую доходность.

Таким образом, стандартное отклонение доходности актива выступает мерой степени и вероятности разброса ее возможных значений вокруг ее средней доходности.

Стандартное отклонение является мерой риска изменения доходности актива. Зная данную величину, инвестор может выбирать между более или менее рискованными бумагами. Например, имеются две акции — А и В. Их средняя доходность одинакова и равна 30%, так как это просто средняя арифметическая их доходностей за определенный период времени. В то же время, стандартное отклонение в расчете на год акции А равно 10%, акции В — 15%. Это означает, что акция В рискованнее бумаги А. Учитывая правило трех сигм, инвестор вправе ожидать, что с вероятностью 68,3% через год он может получить по бумаге А доходность в диапазоне от 20% до 40%, а по бумаге В — от 15% до 45%. Поэтому более консервативный вкладчик выберет бумагу А, а более склонный к риску — бумагу В.

Дисперсию как меру риска ввел в теорию портфеля ценных бумаг основоположник современной теории портфеля Г.Марковец. Определенным недостатком данной меры риска является то, что она одинаково учитывает отклонения в доходности актива от его средней доходности как в сторону увеличения, так и снижения. В то же время инвестора, купившего финансовый актив, беспокоит именно снижение его доходности. Рост доходности по сути не является для него риском. Поэтому позже Г.Марковец предложил в качестве меры риска показатель полудисперсии. Выборочная полудисперсия определяется по формуле:

Формула (1.11) отличается от формулы (1.5) только тем что при расчете показателя полудисперсии учитываются только значения доходности актива, которые меньше его ожидаемой доходности. Таким образом, инвесторы получают представление о риске потерь в более прямой форме, чем при расчете дисперсии. В то же время данная мера риска не всегда будет иметь преимущество по сравнению с дисперсией. Так, если доходность актива распределена нормально, то полудисперсия равна половине дисперсии, поскольку нормальное распределение симметрично относительно своего среднего значения. Поэтому использование в этом случае полудисперсии вместо дисперсии не дает инвестору лучшего представления о риске актива. Соответственно безразлично, какую меру риска рассчитывать. В то же время более удобно использовать дисперсию, так как это более простая для расчета и знакомая из математики многим инвесторам величина.

Использование полудисперсии оправдано в отношении активов, доходность которых не характеризуется нормальным распределением, например производных инструментов.

В заключение данного параграфа следует также отметить, что дисперсию актива можно рассчитывать и на основе прогнозов инвестора в отношении конъюнктуры будущего периода. В этом случае инвестор оценивает возможные сценарии ее развития. На этой основе он прогнозирует значения будущих до-ходностей актива и задает им субъективные вероятности. Например, инвестор полагает, что в будущем периоде актив А принесет доходность гх с вероятностью р<, доходность г2 с вероятностью р2 и т.д. доходность гп с вероятностью рп. Сумма всех вероятностей равна 100%. На основе этих данных по формуле (1.1) рассчитывается средняя доходность актива. Далее дисперсия определяется по формуле:

Источник