Курс лекций «Основы финансового менеджмента»
5.2. Определение средней доходности
В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

n – число видов финансовых инструментов в портфеле;
r i – доходность i -го инструмента;
w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.
Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).
В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.
Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).
Таблица 5.2.1
Динамика доходности акции за 3 года
руб.
Источник
Расчет рыночной доходности
Формула расчета рыночной доходности
Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.
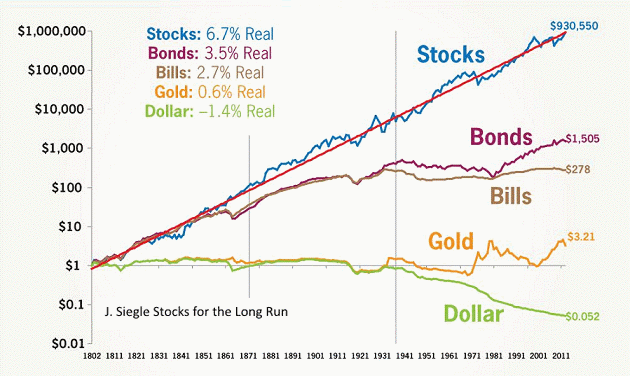
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):
Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.
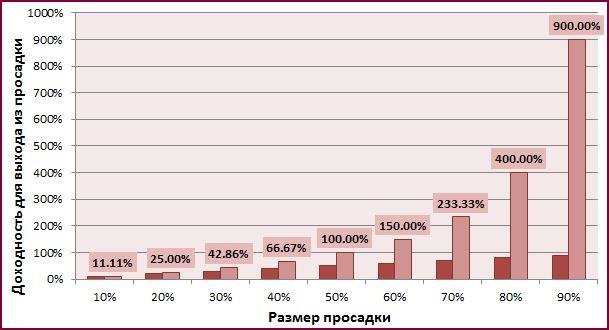
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:
Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.
В общем случае формула доходности выглядит так:
A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1
- A(0) – исходное количество денег
- А(n) – количество денег через n лет
- X – годовая доходность (в процентах)
Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то
A(n) = A(n-1) × Y = A(0) × Y^n
Задача
Актив растет на 10% в год. Какова будет его доходность через 2 года?
Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу
А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)
Обратная задача
Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):
Снова принимая нашу первоначальную доходность за условную единицу, считаем:
Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%
Задача 2
За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?
Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%
Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).
Задача 3
За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?
2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда
Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%
Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.
Задача 4
Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?
Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%
Задача 5
Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.
2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%
Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:
1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)
И средняя инфляция
Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%
P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.
Задача 6
Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?
Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.
Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.
Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).
Задача 7
Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.
Y = [(7.2 + (135-120))/120] × 100% = 18.5%
Задача 8
По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:
Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%
Источник
Средней рыночной ставке доходности
Прирост рыночной Доходность стоимости акции за год + Дивиденд по акции [c.355]
Бета-коэффициент — это измеритель недиверсифицируемого риска, который отражает, как доходность или стоимость конкретного актива реагирует на рыночные силы. Он определяется путем анализа взаимосвязей фактической доходности или рыночной стоимости актива с общей рыночной доходностью — чем выше коэффициент бета, тем выше риск, связанный с активом. [c.124]
Рыночная доходность — это средняя доходность всех или большой выборки активов. [c.125]
Пример. Ценная бумага с коэффициентом бета, равным 1,25, рассматривается в тот момент, когда ставка безрисковых активов составляет 6%, а рыночная доходность — 10%. Подставляя эти данные в уравнение САРМ— уравнение 11.12, получаем Требуемая доходность = 6% + [1,25 х (10% — 6%)] = 11%. Таким образом, инвестору следовало бы ожидать доходности данных инвестиций в 11% в качестве компенсации за риск, который приходится допускать при значении коэффициента бета, рав- [c.125]
Пример. Определить бета-коэффициент обыкновенных акций ОАО. За последние 500 торговых дней на московской фондовой бирже стандартное отклонение доходности акций рассматриваемого ОАО составило 120%, стандартное отклонение индекса доходности рыночной доходности, используемого биржей, составило 140%, коэффициент корреляции между ними составил 0,80. По формуле 11.13 подсчитываем (Зх = 0,8 х (120/140) = 0,68. Оценка риска. Из-за различных предпочтений инвесторов и менеджеров невозможно точно установить общий приемлемый уровень риска. Можно условно подразделить инвесторов и менеджеров на три основные группы по их отношению к риску [c.126]
Например, если предприятие выпускает трехгодичную облигацию номинальной стоимостью 1000 руб. с купонной ставкой 12%, по которой купонные выплаты производятся один раз в год, а ставка дисконтирования, отражающая рыночную доходность аналогичных облигаций, составляет 15%, то предприятие сумеет продать эти облигации по цене 931,5 руб. [c.215]
На рис. 24.4 уровень безрисковой доходности обозначен точкой > Если компания осуществляет более рисковые инвестиции, то этот риск должен быть вознагражден более высокой доходностью — гт. Величина R характеризует размер премии за риск, которая равна разности между уровнем рыночной доходности и ставкой доходности по безрисковым вложениям. Уровень требуемой доходности по конкретному активу (г) определяется по формуле [c.359]
Если безрисковая ставка доходности, в качестве которой можно принять доходность по казначейским векселям США, составляет 5%, уровень рыночной доходности (гт) равен 15%, а коэффициент бета компании А находится на уровне 1,3, то требуемый уровень доходности от инвестиций в акции данной компании определяется следующим образом [c.359]
Страхование процентного риска. Процентный риск возникает при выпуске компанией купонных облигаций и связан с возможностью убытков от снижения процентных ставок. Если выпускаются облигации на длительный период, по которым устанавливается фиксированный купон (например, 20% годовых), а с течением времени происходит снижение процентных ставок (например, до 10% годовых), то компания до конца срока обращения облигаций будет вынуждена выплачивать 20% годовых при рыночной процентной ставке 10%. В данном случае компания несет убытки в связи с выплатой повышенных процентов. Для страхования процентного риска предприятия могут предусмотреть в проспекте эмиссии, во-первых, право досрочного погашения облигаций. Если процентные ставки снизились (в нашем примере с 20 до 10%), то компания, пользуясь своим правом, погашает 20-процентные облигации и выпускает новые облигации, но уже с 10-процентным купоном, соответствующим уровню рыночной доходности. Во-вторых, право установления переменного (плавающего) купона в зависимости от уровня процентных ставок, темпа инфляции, учетной ставки Центрального банка и других параметров, отражающих рыночную стоимость денег. В этом случае в проспекте эмиссии облигаций фиксируется методика расчета купонной ставки. [c.362]
В балансе компании признаются обязательства по взносам без дисконтирования, которые списывают в расход отчетного периода или на увеличение стоимости запасов или основных средств, в соответствии с требованиями МСФО 2 Запасы и МСФО 16 Основные средства . Если начисленные взносы не уплачиваются в течение 12 месяцев после отчетного периода, они должны дисконтироваться по ставкам рыночной доходности надежных облигаций акционерных компаний. Если нормальный рынок таких облигаций отсутствует, ставка дисконтирования определяется по рыночной доходности государственных облигаций на отчетную дату. [c.301]
Ставка дисконтирования должна определяться в соответствии с п. 78 МСФО 19 на основе рыночной доходности высококачественных корпоративных облигаций, зафиксированной по состоянию на отчетную дату. При отсутствии достаточно надежного рынка корпоративных облигаций. Стандарт разрешает использование рыночной доходности государственных облигаций. В случае отсутствия рынка облигаций с длительным периодом обращения, таким как [c.308]
Очевидно, вы должны использовать текущую ожидаемую норму доходности рыночного портфеля, т. е. доходность, от которой отказался бы инвестор, вкладывая средства в предложенный проект. Давайте обозначим эту рыночную доходность через / . Один из способов найти значение гт — предположить, что в будущем ситуация останется практически такой же, как в прошлом, и что сегодня инвесторы ожидают получить такие же «нормальные» нормы доходности, средние значения которых представлены в таблице 7-1. В этом случае вы могли бы взять для г значение 12,1%, среднее значение рыночной доходности в прошлом. [c.141]
Стандартными статистическими показателями разброса результатов служат дисперсия и стандартное отклонение. Дисперсия рыночной доходности представляет собой ожидаемое отклонение от ожидаемой доходности в квадрате. Это можно выразить иначе [c.143]
Но предположим, что мы формируем портфель из большой группы акций со средней бетой, равной 1,5. И опять же мы в конце концов могли бы получить портфель из 500 акций, которые фактически не имели бы индивидуального риска, — портфель, изменчивость которого почти соответствует рыночной. Однако стандартное отклонение такого портфеля оказалось бы равно 30%, т. е. в 1,5 раза больше рыночного отклонения 9. Колебания доходности полностью диверсифицированного портфеля с / = 1,5 будут на 50% больше колебаний рыночной доходности, и риск портфеля окажется равен 150% рыночного риска. [c.155]
Если бы доходность обоих фондов совершенно коррелировала с рыночной доходностью, весь присущий им риск был бы рыночным риском без какого бы то ни было индивидуального риска. В реальной практике полностью диверсифицированных фондов не существует. Это отражают коэффициенты корреляции, которые составляли 0,95 для фонда S-1 и 0,87 для фонда S-4. [c.155]
Предположим, что стандартное отклонение рыночной доходности равно +20%. [c.161]
Ожидаемая доходность акции, если рыночная доходность равна —1 [c.162]
Ожидаемая доходность акции,если рыночная доходность равна +10% [c.162]
Предположим, что ставка по казначейским векселям равна 4%, а ожидаемая рыночная доходность — 10%. Используя информацию из таблицы 8-1 [c.189]
Одна из причин, почему такие оценки бета являются несовершенным ориентиром для будущего, состоит в том, что рыночный риск, присущий акциям, может существенно меняться. Однако более важная причина заключается в том, что бета за какой-либо определенный период — это просто оценка, основанная на ограниченном числе наблюдений. Если позитивная информация о деятельности компании случайно совпадает с высокими значениями рыночной доходности, бета акций будет казаться более высокой, чем когда сообщения о компании совпадают с низкими значениями рыночной доходности. Можно утверждать и обратное. Если значение бета акций оказалось высоким, то, возможно, это потому, что акции действительно имеют высокий коэффициент бета, но также возможно, и из-за того, что мы завысили их оценку. [c.200]
Чтобы найти бету, мы вычисляем ковариацию между доходностью актива и рыночной доходностью и делим это на дисперсию рыночной доходности [c.223]
Это надежный эквивалент, полученный с помощью модели оценки долгосрочных активов. Отсюда следует, что, если активам не присущ риск, ov( ,, г, ) равна нулю и мы просто дисконтируем С, по безрисковой ставке. Но если активы рисковые, мы должны дисконтировать надежный эквивалент С,. Скидка, которую мы делаем с С зависит от рыночной цены риска и ковариации между потоками денежных средств по проекту и рыночной доходностью. [c.224]
Оценочное значение бета проекта равно 1,5. Рыночная доходность гт составляет 16% и безрисковая ставка процента / равна 7%. [c.228]
Рыночная доходность (гт) в январе 1987 г. была равна 13,2% прироста индекса плюс среднемесячная норма дивидендного дохода 0,25%. Процентная ставка (г) составила 5,5 в год, или приблизительно 0,45 в месяц. Следовательно, [c.327]
АЛЬФА = среднее изменение цены на акцию при нулевой рыночной доходности. [c.1046]
Коэффициент «бета » соответствует тому, что в статистике называется коэффициентом Регрессии, при этом рыночная доходность выступает в качестве независимой переменной, а доход- [c.233]
Бета-коэффициент широко используется финансовыми аналитиками-практиками в качестве измерителя недиверсифицируемого риска, связанного с ценными бумагами. В этом случае в качестве меры рыночного дохода используется оценка дохода большой выборки акций, в США, например, часто используют в качестве меры рыночной доходности составной фондовый индекс доходности акций 500 компаний Standard Poor s — S P 500 index . [c.125]
Д,исперсия(7,)- —— где гм — рыночная доходность в период t, г — среднее значение 7 , [c.143]
Здесь, rm— rf— это ожидаемая премия за риск рыночного портфеля, а ст — дисперсия рыночной доходности. Величину Я часто называют рыночной ценой риска. В Приложении к данной главе мы покажем вам происхождение формулы для EQr [c.219]
В главе 7 мы вычисляли ожидаемую рыночную доходность как сумму ставки по казначейским векселям и средней для предшествующих лет премии за риск. Мы получили rm= rf+ обычная премия зариск = 0,08 + 0,084 = 0,164, или 16,4%. [c.322]
Предположим, что для акций компании Eau de Rodman, In , выходящей на рынок с новым видом одеколона, предсказывается стандартное отклонение доходности 0,30 и корреляция ее доходности с доходностью рыночного портфеля 0,9. При стандартном отклонении рыночной доходности (доходности рыночного портфеля), составляющем 0,20, определите процентное содержание рыночного портфеля и доли акций Eau de Rodman в нем, необходимое для получения портфеля ценных бумаг с величиной «бета», равной 1,8. [c.242]
Источник