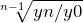Среднегодовые темпы роста инвестиций

CAGR, Среднегодовой темп роста

CAGR — это полезная мера роста инвестиций за несколько периодов времени, особенно если стоимость ваших инвестиций сильно колебалась в течение рассматриваемого периода.

Калькулятор

Чтобы рассчитать CAGR, введите начальное значение, конечное значение и количество периодов, в течение которых инвестиции выросли.

Формула расчёта CAGR

CAGR или совокупный годовой темп роста — это средняя скорость, с которой инвестиции растут с течением времени, предполагая, что их реинвестировали ежегодно (периодически), т.е. с учетом сложного процента. CAGR не имеет ничего общего со стоимостью инвестиций в промежуточные годы, так как она зависит только от стоимости в первый год и последний год инвестиционного владения.

CAGR = (EV / BV) 1/n — 1

• BV — Начальное значение, BV (beginning value)
• EV — Конечное значение, EV (ending value)
• n — Число периодов

Пример

Если ваши инвестиции выросли с 100.000 рублей до 250.000 рублей за последние пять лет, то совокупный годовой темп роста ваших инвестиций составил 20,11% в год. Калькулятор CAGR также можно использовать для определения темпа роста, который вам понадобится в будущем для достижения инвестиционных целей, поставленных сегодня. Например, если у вас сегодня есть 1000 долларов, и через пять лет вы хотите, чтобы ваши инвестиции составляли 2500 долларов, вам нужно будет найти такие способы инвестирования, которые, как ожидается, могут приносить по 20,11% в год.

Где применяется калькулятор CAGR

Среднегодовой темп роста применяется в различных участках личных финансов. Он часто используется для расчета среднего роста отдельных инвестиций за определенный период. CAGR может применяться при сравнении доходности капитала с облигациями или депозитами. Кроме того, его можно использовать для сравнения результатов деятельности двух компаний и прогнозирования их будущего роста на основе их исторических данных.

Ограничение CAGR

CAGR не учитывает волатильность. Он рассчитывает только средний процент возврата, поэтому значения CAGR никогда не должны рассматриваться как единственный инструмент для оценки возврата инвестиций.

Почему CAGR так важен

Хотя среднегодовая доходность является общепринятой для взаимных фондов, CAGR является всё же лучшим показателем доходности инвестиций с течением времени.

Например, мы сделали гипотетическое инвестирование 1000 рублей в какой-то фонд или вообще во что-то (куда — не важно). Прошло два года. В конце первого года стоимость портфеля упала с 1000 до 750 рублей, т.е. получается доходность -25% [(750–1000) / 1000]. А затем, к концу второго года стоимость портфеля выросла на +33% [(1000 — 750) / 750].

Усреднение результатов за 1-й и 2-й год за два года дает нам среднюю доходность 4% [(-25 + 33) / 2], но это не совсем точно отражает то, что произошло на самом деле. Мы начали с 1000 рублей и закончили тоже на 1000 рублей, а значит наша доходность равна 0%.

Т.е. ещё раз. В данном примере, среднегодовая доходность: 4%, а CAGR равен 0%, что конечно правильнее.

Источник

Формула среднегодового темпа роста

Понятие темпа роста

Математическая статистика часто использует формулу темпа роста. Темп роста определяет интенсивность изменения (динамики) определенного явления.

Для того, что бы определить темп роста требуются следующие показатели:

• Начальный показатель,
• Базисный показатель,
• Несколько промежуточных показателей, которые измеряются равными интервалами.

Для расчета среднегодового темпа роста применяется временной интервал, который равен месяцу.

Понятие темп роста применяется во многих сферах (экономика, финансы, статистика, промышленность и др.). Темп роста является статистической величиной, позволяющей провести анализ:

• Динамики определенного процесса,
• Скорость развития,
• Интенсивность развития определенного явления и др.

Для вычисления темпа роста происходит сравнение значений, которые получены через выбранные промежутки времени.

Формула темпа роста

В общем виде, при наличии базисного и текущего показателя, формула темпа роста выглядит следующим образом:

Тр=Птек/Пбаз

Здесь Тр – темп роста,

Птек – показатель текущего периода,

Пкп – показатель базисного периода.

Что бы получить более наглядный результат, полученный ответ умножают на 100%, что позволяет выразить темп роста в процентах.

Порядок расчета среднегодового темпа роста

Для расчета среднего темпа роста требуется определить период, за который он будет рассчитан. В большинстве случаев таким периодом является календарный год или показатель, кратный ему.

Темп роста является относительным понятием, поскольку определяет изменение определенных величин по отношению к какому-либо начальному значению. Для расчета среднегодового темпа роста определяется начальное значение на 1 января исследуемого года. Расчет среднегодового темпа роста может проводиться в соответствии с величинами:

• Базисными (показывают отношение изменений величин по отношению к базисному значению);
• Цепными (показывают интенсивность изменения величин соседних периодов или дат).

Общая формула расчета среднегодового темпа роста выглядит следующим образом:

Тр ср =

Здесь n– количество месяцев (лет),

y0 – базисный показатель (например, на 1 января)

Особенности формулы среднегодового темпа роста

Формула среднегодового темпа роста использует в качестве базисного показателя численную величину, которая характеризует изучаемое явление и определяется по концу предыдущего года. Таким образом, базисная величина – это величина показателя на 1 января того года, для которого требуется определить темп роста.

При расчете формулы среднегодового темпа роста коэффициентом, базовый показатель принимают за единицу или 100 (если расчет осуществляется в процентах). В процессе вычисления базовых темпов роста на каждый месяц в году все показатели по окончанию каждого месяца должны соотноситься с базовым показателем (на 1 января).

При определении цепных показателей, за базовый показатель принимается показатель предыдущего периода, поэтому при расчете формула среднегодового темпа роста удобнее рассчитывается с помощью цепных показателей.

Значение среднегодового темпа прироста

За анализируемый период формула среднегодового темпа роста принимает календарный год, то есть промежуток с 1 января по 31 декабря. Для этого необходимы данные в абсолютном значении на конец каждого месяца. Всего должно быть 13 значение (базовый показатель и 12 показателей за каждый месяц).

Формула среднегодового темпа роста имеет значение, поскольку при ее расчете по нескольким годам можно получить результат для дальнейшего анализа и учета сезонных колебаний. Сам среднегодовой темп роста свободен от влияния фактора сезонности.

Примеры решения задач

Задание

Рассчитайте среднегодовой темп роста по показателям, представленным за год:

Январь – 240, февраль – 256, март – 258, апрель – 259, май – 262, июнь – 275, июль – 278, август – 279, сентябрь – 282, октябрь – 284, Ноябрь – 288, декабрь – 291.

Решение Рассчитаем средний уровень ряда динамики:

Пср = (240+256+258+259+262+275+278+279+282+284+288+291) / 12 = 271 – среднее значение с 1 по 12 месяц.

Формула среднегодового темпа роста для решения данной задачи:

Тр ср =

Тр ср =

Ответ Трср = 1,018

Задание

Рассчитать среднегодовой темп роста и прироста, по условным данным объема импорта государства:

2011 год – 250 усл. ед.,

2012 год – 258усл. ед.,

2013 год – 262усл. ед.,

2014 год – 248усл. ед.,

2015 год – 259усл. ед.,

2016 год – 268усл. ед.,

Решение Формула среднегодового темпа роста для решения данной задачи:

Тр ср =

Тр ср =

Вывод:За период с 2011 по 2016 год ежегодно объем импорта государства в среднем возрастал на 1,014 единиц.

Источник

Среднегодовой темп роста (AAGR)

Что такое Среднегодовой темп роста (AAGR)?

Среднегодовой темп роста (AAGR) – это средний рост стоимости отдельной инвестиции, портфеля, актива или денежного потока за период года. Он рассчитывается путем взятия среднего арифметического ряда темпов роста. Среднегодовой темп роста может быть рассчитан для любой инвестиции, но он не будет включать в себя какую-либо меру общего риска инвестиции, измеряемого по ее волатильности.

Среднегодовой темп роста используется во многих областях исследований. Например, в экономике он используется для получения лучшего представления об изменениях в экономической активности (например, темпах роста реального ВВП).

Ключевые моменты

• Этот коэффициент помогает вам определить, сколько в среднем вы получили за несколько периодов времени.
• AAGR рассчитывается путем взятия среднего арифметического ряда темпов роста.
• AAGR – это линейная мера, которая не учитывает эффекты начисления процентов.

Формула для среднегодового темпа роста (AAGR):

ААгрзнак равногрА+грB+…+грпNжчере:грАзнак равноСтоштч ттеяпрегяод грBзнак равноСтоштч ттеяпрегяодБ грпзнак равноСтоштч ттеяпрегяод пNзнак равноNumber of payments\ begin & AAGR = \ frac \\ & \ textbf <где:>\\ & GR_A = \ text <Скорость роста в период A>\\ & GR_B = \ text <Скорость роста в периоде B>\\ & GR_n = \ text <Скорость роста в периоде>n \\ & N = \ text <Количество платежей>\\ \ end <выровнено>Взаимодействие с другими людьмиААГРзнак равноN

Как рассчитать AAGR

AAGR – стандарт для измерения средней доходности инвестиций за несколько периодов времени. Вы найдете эту цифру в брокерских отчетах, и она включена в проспект паевого инвестиционного фонда. По сути, это простое среднее значение ряда периодических темпов роста доходности. Следует иметь в виду, что все используемые периоды должны быть одинаковой продолжительности, например годы, месяцы или недели, и не смешивать периоды разной продолжительности.

Что вам говорит AAGR?

Среднегодовой темп роста помогает определить долгосрочные тенденции. Это применимо практически к любым финансовым показателям, включая темпы роста прибыли, доходов, денежных потоков, расходов и т. Д., Чтобы дать инвесторам представление о направлении, в котором движется компания. Этот коэффициент показывает, какой в ​​среднем была ваша годовая доходность.

Среднегодовой темп роста может быть рассчитан для любой инвестиции, но он не будет включать в себя какую-либо меру общего риска инвестиции, измеряемого по ее волатильности. Более того, AAGR не учитывает периодическое начисление сложных процентов.

Пример использования среднегодового темпа роста (AAGR)

AAGR измеряет среднюю норму прибыли или роста за серию равномерно распределенных периодов времени. В качестве примера предположим, что в течение четырех лет инвестиция имеет следующие значения:

• Начальное значение = 100 000 долларов США.
• Стоимость на конец года 1 = 120 000 долларов США.
• Стоимость на конец 2 года = 135 000 долларов США.
• Стоимость на конец 3 года = 160 000 долларов США.
• Стоимость на конец 4-го года = 200 000 долларов США.

Формула для определения процентного роста за каждый год:

• Sятрле ретсентгеггоштчотретутп знак равноэндинг валуебегиннинг валуе-1\ text <Простой рост или доходность в процентах>= \ frac <\ text <конечное значение>><\ text <начальное значение>> – 1Простой процентный рост или доходностьзнак равноначальное значение

Таким образом, темпы роста за каждый год следующие:

• Рост за 1 год = 120 000 долл. США / 100 000 долл. США – 1 = 20%
• Рост за 2-й год = 135 000 долларов США / 120 000 долларов США – 1 = 12,5%
• Рост за 3 год = 160 000 долл. США / 135 000 долл. США – 1 = 18,5%
• Рост за 4 год = 200 000 долл. США / 160 000 долл. США – 1 = 25%

AAGR рассчитывается как сумма темпов роста за каждый год, деленная на количество лет:

• ААгрзнак равно20%+12.5%+18.5%+25%4знак равно19%AAGR = \ frac <20 \% + 12,5 18,5 25><4>= 19 \%ААГРзнак равно4

В финансовых и бухгалтерских настройках обычно используются начальная и конечная цены, но некоторые аналитики могут предпочесть использовать средние цены при расчете AAGR в зависимости от того, что анализируется.

Среднегодовой темп роста по сравнению со сложным годовым темпом роста

AAGR – это линейная мера, которая не учитывает эффекты начисления процентов. Приведенный выше пример показывает, что инвестиции росли в среднем на 19% в год. Среднегодовой темп роста полезен для отображения тенденций; однако он может ввести аналитиков в заблуждение, поскольку не точно отражает изменение финансовых показателей. В некоторых случаях он может переоценить рост инвестиций.

Например, рассмотрим значение на конец года для 5-го года в размере 100 000 долларов. Процентный темп роста за 5-й год составляет -50%. В результате AAGR составит 5,2%; однако из начального значения 1-го года и конечного значения 5-го года очевидно, что результативность дает 0% прибыли. В зависимости от ситуации может оказаться более полезным рассчитать среднегодовой темп роста (CAGR). CAGR сглаживает доходность инвестиций или уменьшает влияние волатильности периодической доходности.

Формула CAGR:

CАгрзнак равноЭндинг БаланцеБегиннинг Балансе1# Years-1CAGR = \ frac <\ text <Конечный баланс>> <\ text <Начальный баланс>> ^ <\ frac <1><\ text <\ # Years>>> – 1CAGRзнак равноВступительное сальдо

Используя приведенный выше пример для лет с 1 по 4, CAGR равен:

CАгрзнак равно$200,000$100,00014-1знак равно18.92%CAGR = \ frac <\ 200 000> <\ 100 000>^ <\ frac <1><4>> – 1 = 18,92 \%CAGRзнак равно$100,000

В течение первых четырех лет AAGR и CAGR близки друг к другу. Однако, если бы год 5 был включен в уравнение CAGR (-50%), результат был бы равен 0%, что резко контрастирует с результатом AAGR в 5,2%.

Ограничения среднегодового темпа роста (AAGR)

Поскольку AAGR представляет собой простое среднее значение периодической годовой доходности, эта мера не включает в себя какой-либо показатель общего риска, связанного с инвестициями, рассчитанного на основе волатильности их цены. Например, если портфель вырастет на чистую величину в 15% за один год и на 25% в следующем году, средний годовой темп роста будет рассчитан как 20%. С этой целью колебания нормы прибыли от инвестиций в период с начала первого года до конца года не учитываются в расчетах, что приводит к некоторым ошибкам в оценке.

Вторая проблема заключается в том, что в качестве простого среднего значения не важны сроки возврата. Например, в нашем примере выше резкое снижение на 50% в 5-м году имеет лишь умеренное влияние на общий среднегодовой рост. Однако выбор времени важен, и поэтому CAGR может быть более полезным для понимания того, насколько важны темпы роста, привязанные ко времени.

Источник