Среднегодовая доходность финансовой операции

Правильный расчет среднегодовой доходности в инвестициях

Любой инвестор рано или поздно должен подвести итоги и рассчитать доходность инвестиций. Так как цифры вроде 125% за 5 лет мало информативны, то доходность принято приводить доходность к годовым значениям. Такую доходность называют среднегодовой доходностью. В случае с 125% за 5 лет среднегодовая доходность равна 17,6%. 125% принято назвать накопленной доходностью.

Как рассчитать среднегодовую доходность

Если период инвестиций измеряется в годах, то формула среднегодовой доходности выглядит следующим образом:

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в годах)

Эта формула предполагает капитализацию процентов. Её нельзя применять, например, в тех случаях, когда дивиденды выводились из инвестиций (не реинвестировались).

В случае произвольного промежутка инвестиций среднегодовая доходность считается по аналогии.

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в месяцах)

Здесь период инвестиций измеряется в месяцах. Если необходимо рассчитать с точностью до дней, то 12 надо заменить на 365.

Пример вычисления:

Инвестор получил доходность 12% за 16 месяцев. Чему равна его годовая доходность?

Основные ошибки при вычислениях

Чаще всего начинающие инвесторы допускают ошибку, считая следующим образом (пример с доходностью 125% за 5 лет):

Или в примере с 12% за 16 месяцев:

Такой вариант расчетов в инвестициях использовать нельзя, так как при этом не учитывается капитализация процентов.

Источник

Курс лекций «Основы финансового менеджмента»

5.2. Определение средней доходности

В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

, где (5.2.1)

n – число видов финансовых инструментов в портфеле;

r i – доходность i -го инструмента;

w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.

Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).

В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.

Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).

Таблица 5.2.1
Динамика доходности акции за 3 года
руб.

Источник

Доходность финансовой операции

Доходность и риск финансовой операции

Краткое содержание раздела:

Доходность финансовой операции. Доходность за несколько периодов. Синергетический эффект.

Риск финансовой операции. Количественная оценка риска финансовой операции. Коррелированность финансовых операций. Другие меры риска. Стоимость под риском (Value at risk, VaR). Виды финансовых рисков. Методы уменьшения риска финансовых операций (диверсификация, хеджирование, опционы, страхование).

Финансовые операции в условиях неопределенности. Матрицы последствий и рисков. Принятие решений в условиях полной неопределенности. Пpaвила Вальда, Сэвиджа, Гурвица. Принятие решений в условиях частичной неопределенности. Правило максимизации среднего ожидаемого дохода. Правило минимизации сpeднeгo oжидaeмoгo pиcка. Оптимальная (по Парето) финансовая операция. Правило Лапласа равновозможности.

Доходность финансовой операции

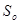
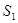
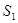
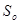
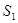
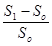
Финансовой называется любая операция, начальное и конечное состояние которой имеет финансовое (денежное) выражение. Одной из главных целей проведения любой финансовой операции является получение максимальной прибыли. Поэтому прибыль ( — ) – одна из основных характеристик финансовой операции, наряду с полученным в результате ее доходом . Более точно финансовую операцию характеризует ее доходность (или эффективность) .

Доходы от финансово-кредитных операций и различных коммерческих сделок имеют различную форму: проценты от выдачи ссуд, комиссионные, дисконт при учете векселей, доходы от облигаций и других ценных бумаг и т.д. Само понятие «доход» определяется конкретным содержанием операции. При чем, в одной операции часто предусматривается два, а то и три источника дохода (например, проценты и комиссионные). Поэтому возникает проблема измерения доходности операции с учетом всех источников поступлений.

Обобщенная характеристика доходности должна быть сопоставимой и применима к любым видам операций и ценных бумаг. Обычно степень финансовой эффективности (доходности) этих операций измеряется в виде годовой ставки процентов. Искомые показатели получают исходя из общего принципа – все вложения и доходы с учетом конкретного их вида условно приравниваются эквивалентной (равнодоходной) ссудной операции.

Решение проблемы измерения и сравнения степени доходности финансово-кредитных операций заключается в разработке методик расчета условной годовой ставки для каждого вида операций с учетом особенностей соответствующих контрактов и условий их выполнения.

Расчетная процентная ставка, о которой идет речь, получила различные названия. В простых депозитных и ссудных операциях она называется эффективной, в расчетах по оценке облигаций ее часто называют полной доходностью, или доходностью на момент погашения. В анализе производственных инвестиций для аналогичного по содержанию показателя применяется термин внутренняя норма доходности или внутренняя норма процента.

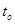
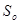
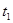
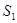
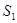
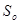
Доходность сделки за период. Пусть в некоторый начальный момент времени инвестор располагает суммой , которая представляет собой его начальный инвестиционный капитал. Разместив тем или иным образом этот капитал на некоторое время или инвестиционный период, он к концу этого периода будет обладать суммой , представляющей общий результат инвестиционной операции за указанный период. В благоприятном случае, т.е. при > , говорят, что инвестор получает инвестиционный доход

I= — ;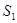

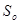
в противном случае, т.е. при

.

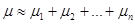
Более точное выражение имеет вид:

. (1)

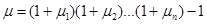
Доказательство приведенной формулы можно найти в учебном пособии П.Н. Брусов и др. «Финансовая математика», с. 105, п. 3.1.1.

Синергетический эффект. Синерги?я (греч. συνεργ?α — сотрудничество, содействие, помощь, соучастие, сообщничество) — суммирующий эффект взаимодействия двух или более факторов, характеризующийся тем, что их действие существенно превосходит эффект каждого отдельного компонента в виде их простой суммы, эмерджентность.

Например: прибыль после слияния двух компаний может превосходить сумму прибылей этих компаний до объединения.

Синергетический эффект – возрастание эффективности деятельности в результате интеграции, слияния отдельных частей в единую систему за счет т. н. системного эффекта (эмерджентности).

В бизнесе это совместное действие для достижения общей цели, основанное на принципе, что целое представляет нечто большее, чем сумма его частей. Так, например, доходы от совместного использования ресурсов превышают сумму доходов от использования тех же ресурсов по отдельности. Синергетический эффект в деятельности компании может возникнуть в результате интеграции, слияния отдельных частей в единую систему. Синергетический эффект еще называют эффектом 2+2=5.

Финансовая синергия – это экономия за счет изменения источников финансирования, стоимости финансирования и прочих выгод.

Финансовая синергия дает компании следующие выгоды:

1. При объединении двух денежных потоков уменьшается их волатильность, снижаются риски, укрепляется платежеспособность и сокращается необходимость в заемных средствах.

2. Более низкий риск способствует снижению процентной ставки при заимствовании.

Полученный синергетический эффект способствует процветанию компании и помогает ей создавать ценности большие, чем ценности конкурентов.

Синергетический эффект в случае оценки доходности за несколько периодов приводит к тому, что доходность за несколько последовательных периодов времени оказывается больше простой суммы доходностей.

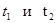
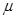
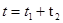
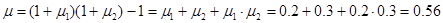
Пример. Пусть доходности за два последовательных периода времени равны соответственно 20 и 30%. Тогда по формуле (1) доходность за период равна

,

т.е. 56%. Таким образом, отличие от суммы доходностей составляет 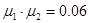или 6%.

Источник