Среднее взвешенное доходность формула

Курс лекций «Основы финансового менеджмента»

5.2. Определение средней доходности

В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

, где (5.2.1)

n – число видов финансовых инструментов в портфеле;

r i – доходность i -го инструмента;

w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.

Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).

В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.

Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).

Таблица 5.2.1
Динамика доходности акции за 3 года
руб.

Источник

Оценка доходности портфелей облигаций

Для оценки доходности портфелей облигаций чаще всего используются следующие две меры доходности: средневзвешенная доходность и внутренняя доходность.

Средневзвешенная доходность портфеля облигаций

Средневзвешенная доходность портфеля облигаций (weighted average portfolio yield) определяется по формуле:

где k – число облигаций в портфеле;

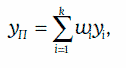
yi – доходность i-й облигации, i = 1, 2, …, k;

wi – отношение рыночной стоимости i-й облигации к рыночной стоимости всего портфеля, i = 1, 2, …, k.

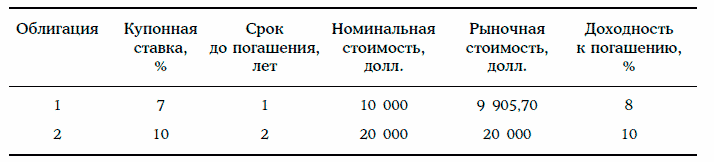
Пример 1. Портфель состоит из двух облигаций с полугодовыми купонами, параметры которых указаны в таблице:

Определим средневзвешенную доходность портфеля облигаций. В данном случае

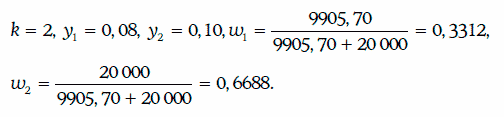
Следовательно, средневзвешенная доходность портфеля равна

yп = 0,3312 • 0,08 + 0,6688 • 0,10 = 0,0934, т. е. 9,34 %.

Внутренняя доходность портфеля облигаций

Внутренней доходностью портфеля облигаций (portfolio internal rate of return) является процентная ставка, при которой приведенная стоимость потока платежей от портфеля совпадает с рыночной стоимостью этого портфеля. Следовательно, чтобы определить внутреннюю доходность портфеля облигаций, предварительно необходимо найти поток платежей по данному портфелю.

Пример 2. Найдем внутреннюю доходность портфеля облигаций из примера 1.

Поток платежей по рассматриваемому портфелю имеет следующий вид:

Следовательно, внутренняя доходность портфеля облигаций должна удовлетворять уравнению:

Значит, у = 0,0959.

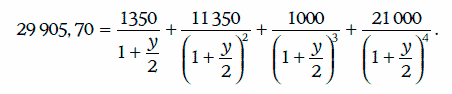
Таким образом, внутренняя доходность портфеля облигаций составляет 9,59 %.

Источник

Результаты управления: Измерение доходности — 2

В продолжение предыдущего поста.

Доходность, взвешенная по времени.

Отражает рост каждого рубля на счету. Для этого нужно, соответственно, знать точно дату, когда пришел этот «каждый рубль», т.е. необходимо пересчитывать стоимость портфеля при каждом внесении (выводе). Довольно трудоемко, но зато точно. В связи с этим Глобальные стандарты оценки результатов инвестирования предпочитают именно этот расчет.

Сама формула выглядит так 1 + r_t = [(1 + r_t,1) * (1 + r_t,2) * … * (1 + r_t,n)] 1/ n , где r_t и есть доходность нашего портфеля, а r_t,n представляет собой доходность за периоды между внесением (выводом) средств.

Пример. На начало месяца у меня 2,500,000 рублей на счете, в конце 2,700,000. 7-го числа я внес 45,000 рублей и 19-го — 25,000, при этом стоимость портфеля на эти даты 2,555,000 и 2,575,000 соответственно:

r_t,1= ((2,555,000 − 45,000) − 2,500,000) / 2,500,000 = 0.4%

Второй субпериод (8−19).
r_t,2 = ((2,575,000 − 25,000) − 2,555,000) / 2,555,000 = −0.2%

Третий (20−30 дней).
r_t,3 = (2,700,000 − 2,575,000) / 2,575,000 = 4.9%

Итого получаем, склеив все субпериоды, r_t = (1 + 0.004) * (1 − 0.002) * (1 + 0.049) – 1 = 5.1% за месяц из 30 дней.

Доходность, взвешенная по деньгам. Здесь ситуация несколько сложнее, т.к. потребуется расчет внутренней нормы доходности (IRR) либо на калькуляторе, либо в экселе. Зато менее затратная в плане отсутствия необходимости высматривать все входящие и исходящие средства клиентов, но и менее точная поэтому.

Например. На начало месяца у меня 900,000 на счете, 15-го числа я вношу еще 50,000. И в конце месяца у меня 1,466,553. Считаем так: 1,466,553 = 900,000 * (1 + IRR) 2 + 50,000 * (1 + IRR), отсюда IRR = 24.9% за 15 дней (!), что составляет (1.24904 2 – 1) = 56.01% в месяц.

Сравнение обоих методов.

Клиент инвестировал 100,000 в начале года, на конец года стоимость активов возросла до 105,000. Доходность по обоим методам составить 5%. Клиент вносит еще 95,000, т.е. общая стоимость портфеля на начало втророго года получается 200,000 и увеличивается к концу до 220,000. Доходность по второму году уже 10%. Сколько за 2 года?

Взвешенная по времени r_t = (1.05 * 1.10) 1/2 – 1 = 7.47% в год или 15.50% за два.

Взвешенная по деньгам 100,000 * (1 + r_t) 2 + 95,000 * (1 + r_t) 1 = 220,000 и r_t = 8.24% или (1.0824 2 – 1) = 17.16% за два.

Я, кстати, планирую опустить требования к бенчмарку, против которого надо оценивать доходность портфеля. Если надо, конечно, могу и написать 🙂 Получается, что в следующем посте будет определять источник нашей доходности.

Источник

Блог Александра Кашина об инвестициях

Инвестиции, пассивный доход и финансовая независимость

Доходность портфеля (методика расчета)

— существует 2 основных метода расчета доходности портфеля: простой и средневзвешенный. Простой метод применяется лишь для экспресс-анализа портфеля (куда идет в целом портфель, стало больше или меньше), потому что содержит математически не корректные данные. Средневзвешенная доходность рассчитывается по итогам отчетного периода (например, года) и является корректным показателем.

Простая доходность

рассчитывается по формуле = (Стоимость портфеля в конце периода / Сумма вложений за весь срок существования портфеля)- 1.

О том, почему такой расчет не корректен при наличии пополнений портфеля см. здесь.

Средневзвешенная доходность

Ее рассчитать сложнее, поэтому и делаем мы это реже (обычно раз в год).

Для ее расчета нужно вычислить средневзвешенную стоимость портфеля в течение года. А потом использовать следующую формулу

(Прибыль или убыток за период / Средневзвешенная стоимость портфеля в течение периода) — 1

Для того, чтобы рассчитать средневзвешенную стоимость портфеля нужно:

• разделить год на периоды по количеству доп. взносов в портфель.
• стоимость портфеля в каждом периоде умножить на количество дней этого периода
• сложить суммы по всем периодам
• разделить итоговую сумму на количество дней в периоде

Источник

Как правильно рассчитать доходность?

«Сегодняшний инвестор не получает прибыль от вчерашнего роста»(Уоррен Эдвард Баффетт)

Сейчас я подвожу итоги первого года своего публичного проекта «Разумный инвестор». Скоро опубликую, особо не тороплюсь, так как до осени ничего не собираюсь предпринимать — ни покупать, ни продавать…

Весь год я определял доходность моего портфеля по методике, которую используют ПИФы, при расчете стоимости паев. В принципе, это правильно, но только для цены паёв. Результат конкретного инвестора будут совсем иным.

Есть один нюанс, который всё усложняет в вопросе определения доходности. Это операции ввода/вывода!

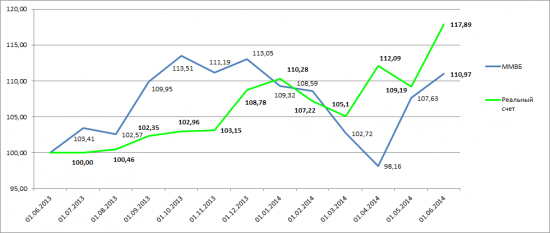
Ранее озвученный мой результат +17,89%,оказался неверным (точнее это не моя доходность, а изменение стоимости пая – если мой портфель был бы ПИФом и я брал деньги в управление у пайщиков).

Так как я производил регулярные инвестиции, а также два раза выводил средства, то использовать данный метод уже нельзя, он искажает реально полученную доходность. Реальная доходность получилась +23,78% годовых (как раз скучные 24% годовых, которые на этих выходных обсуждали на сМарт-Лабе)))

Думаю, многим будет полезно прочесть данный пост. Я до недавнего времени даже не знал этой информации, мне казалось, что применяемый способ вполне приемлем.

«Как рассчитать доходность?», на первый взгляд этот вопрос не должен вызывать ни малейшего затруднения. Многие знают, что для того чтобы посчитать доходность, необходимо результат инвестиций разделить на сумму вложенных средств и перевести полученное значение в проценты годовые.

Формула расчета доходности (в процентах годовых), если не происходило вводов/выводов:

D = ((ΔS)/Sнач) * 365/T * 100%, где

D – искомая доходность,

ΔS – результат инвестирования в абсолюте,

Sнач – сумма первоначальных инвестиций,

T – количество дней в рассматриваемом периоде.

Но задача расчета доходности многократно усложняется в случае, если в течение рассматриваемого периода осуществлялись вводы или выводы средств в рамках инвестиционного портфеля. В таком виде она вызывает затруднения даже у опытных специалистов в области инвестиций.

Решение данной задачи мне подсказали мои коллеги из УК Арсагера

Немного теории:

Начнем с определения того, что же такое вводы и выводы денежных средств. Ввод денежных средств – это направление денег на инвестиции. К примеру, Вы приобрели инвестиционные паи фонда или внесли деньги на брокерский счет – все это является вводом средств. Изъятие инвестиционных средств является выводом, то есть, в рамках примеров, выводы возникают при погашении инвестиционных паев или выводе денег с брокерского счета.

Зная, что же такое вводы/выводы, рассмотрим конкретную ситуацию, которая поможет понять логику решения задачи по корректному определению доходности с учетом вводов/выводов средств.

Некий инвестор приобрел акций на сумму в 1000 рублей (Sнач).

Через 3 месяца он купил еще акций на 500 рублей (Sвв).

Еще через 4 месяца инвестору срочно понадобились деньги, и он был вынужден продать часть акций на сумму в 300 рублей (Sвыв).

Через год после первоначального приобретения, стоимость акций составила 1300 рублей (Sитог).

В виде графика данную ситуацию можно представить следующим образом:

Чтобы корректно рассчитать доходность от инвестиций нам по-прежнему необходимо разделить результат инвестиций на сумму вложенных средств. Остается только определить, что в рассматриваемой ситуации является результатом и какова корректная сумма вложенных средств.

Первым шагом будет расчет результата инвестиций. Интуитивно понятно, что результат инвестиций это разница между теми средствами, которые были получены, и теми, которые были вложены. То есть, необходимо из суммы итоговой стоимости инвестиций и всех выводов вычесть сумму начального и последующих вводов.

Формула для определения результата инвестирования с учетом вводов/выводов:

ΔS = (Sитог + ΣSвыв) – (Sнач + ΣSвв), где

ΔS – результат инвестирования за период в абсолюте,

Sитог – итоговая оценка инвестиций (1 300),

ΣSвыв – сумма всех выводов средств (300),

Sнач – сумма первоначальных инвестиций (1 000),

ΣSвв – сумма всех вводов средств (500).

Применим данную формулу к рассмотренной ситуации: ΔS = (1300 + 300) – (1000 + 500) = 100. Таким образом, инвестор заработал 100 рублей.

Второй шаг в расчете доходности является наиболее важным: необходимо корректно определить с какой суммой соотносить рассчитанный результат инвестирования, то есть корректно определить сумму вложенных средств.

В каждый временной подпериод (T1, T2, T3) сумма вложенных средств была разной. В подпериод T1 – 1000 рублей, T2 – (1000+500) рублей, T3 – (1000+500-300) рублей. Кроме того, сами по себе эти временные подпериоды не равны. T1 – 90 дней, T2 – 120 дней, T3 – 155 дней. Поэтому необходимо согласовать суммы вложенных средств с количеством дней в подпериоде, определив таким образом среднюю «рабочую» сумму (средневзвешенную по времени сумму вложенных средств) на рассматриваемом периоде.

Формула для определения средневзвешенной суммы вложенных средств с учетом вводов/выводов:

V = (T1*Sнач+T2*(Sнач+Sвв)+T3*(Sнач+Sвв-Sвыв)+…+Tn*(Sнач+ΣSвв-ΣSвыв)/ ΣT, где

V – средневзвешенная сумма вложенных средств,

T1, T2, T3,Tn – количество дней в подпериоде,

ΣT – суммарное количество дней на рассматриваемом временном отрезке.

Применим данную формулу к рассмотренной ситуации: V = (90*1000 + 120*(1000+500) + 155*(1000+500-300))/365 = 1249,32.

Средневзвешенная сумма вложенных инвестором средств составила 1249,32 рублей.

Теперь известны все элементы, необходимые для непосредственного расчета доходности.

Третий шаг – расчет доходности из полученных значений. Для этого поделим рассчитанный ранее результат инвестирования на средневзвешенную сумму вложенных средств и переведем полученный результат в проценты годовые.

Формула следующая: D = (ΔS/V) * 365/T * 100%

Получается, что в рассмотренной ситуации доходность составляет: (100/1249,32) * 365/365 * 100% = 8% годовых.

Используя данные формулы, Вы всегда сможете корректно оценить доходность Вашего инвестиционного портфеля и при помощи полученных значений оценить эффективность Ваших инвестиций.

Рассмотренный алгоритм не является простым, но когда дело касается расчета доходности и прибыли, то главное – это точность. Данный алгоритм позволяет учесть все нюансы, связанные с вводами/выводами средств и получить корректный расчет доходности.

Если Вы пользуетесь услугами доверительного управления, узнайте, каким образом происходит расчет прибыли и доходности по Вашему портфелю и, если он отличается от обозначенного выше алгоритма, то это повод проверить корректность применяемого алгоритма.

Необходимо внимательно относится к расчету доходности Ваших инвестиций, так как этот показатель является определяющим при проведении анализа эффективности инвестирования и, если он будет рассчитан неверно, то это создаст неверное представление об эффективности Ваших инвестиций.

Теперь практический расчет по моему портфелю.

Как я писал ранее, я считал изменения портфеля по методу «ПИФов», т.е. при вводе новых средств я определял новое СЧА и делил на «стоимость пая» до ввода средств, тем самым увеличивал кол-во паёв для непрерывного продолжения графика стоимости портфеля.

По факту я рассчитывал изменение «цены пая», но это не реальная доходность моих инвестиций, так как этот метод не учитывает суммы ввода/вывода средств. Я мог вводить новые деньги при просадках, и выводить на пиках, и по итогам график «цены пая» мог быть в нуле – а результат инвестиций в хорошем плюсе.

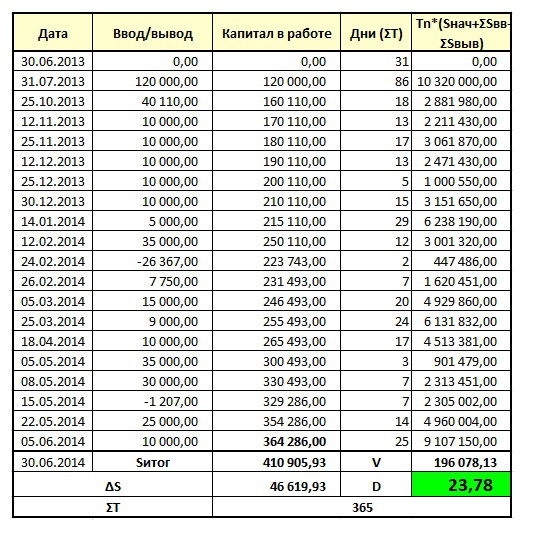
Произведу расчеты доходности по портфелю по формуле приведенной выше, с учетом всех вводов/выводов и дат совершения операций, а также итогового финансового результата:

Получилось +23,78% годовых.

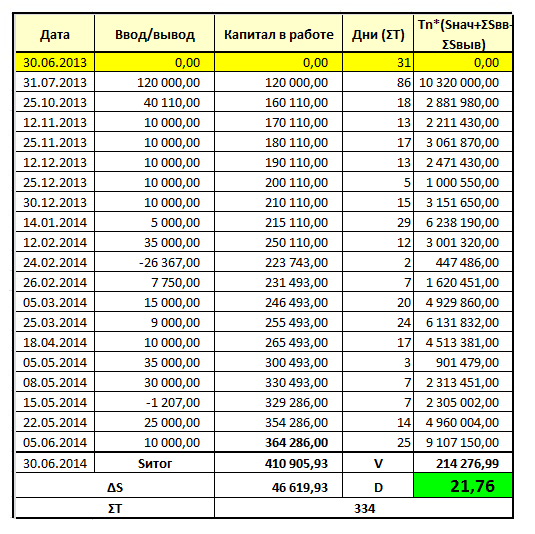
Если посчитать с момента первого ввода средств 31 июля 2013 года.

+21,76% за 334 дней – в годовых (за 365 дней) это +23,78%. Так что всё правильно посчитал.

Довольно значимое искажение – 24% или 18% — есть разница! Если Вы управляете активами и за год не вводите и не выводите средств, то определение доходности по методики «ПИФов» подходит, но, если Вы вводите и выводите средства, то не использовать данный метод – обманывать самого себя или своего инвестора!

Кстати, некоторые ушлые управляющие, показывая свой эквити на истории прибегают к такой хитрости – имея мегарезультат на малой сумме, а позже когда инвесторы вводят более значимые деньги – результат может ухудшиться, но эквити всё равно будет привлекательным для новых инвесторов.

Например, рост эквити в 5 раз за 2 года, из которых за первый год эквити увеличился в 4,5 раза при начальном капитале в 100 тысяч рублей, а потом в конце первого года внесли еще 50 млн. рублей, и результат за второй год был всего лишь +11%, но на эквити за 2 года будет красивый рост в 5 раз!

По методике определения «цены пая» будет всё красиво, а по реальной доходности для инвестора – значительнее скромнее. Рекомендую быть внимательнее к таким моментам…

А какой способ используете Вы ?

Оба метода можно и нужно использовать – но для разных целей, это Вы должны понимать. Если Вы ПИФ (или ИДУ) и берете деньги в управление – определение стоимости пая необходимо, но кроме этого, нужно определять доходность каждого конкретного инвестора. Она будет различаться в зависимости от его операций по вводу/выводу средств.

P.S. Кстати, из-за этого нюанса иногда происходит ошибочное определение результата доходности у конкретного инвестора, что приводит к заблуждениям из-за этого.

Яркий пример – Элвис Марламов, который этой весной вносил средства для покупки акций на провале рынка. Его даже обвиняли в этом? Разве ввод/вывод средств – это зло для инвестора?

Считаю, что это плюс управляющему – умение в нужный момент нажать на газ. Использование плеча – я оставлю за скобками, это дело каждого, я бы не стал его использовать. Но ввод средств для покупки неадекватно дешевых активов – это гуд.

Он сделал всё правильно! Заработал на этой панике.

Но его эквити публичных счетов – всё также внизу. Как такое может быть? Даже пишут, что Элвис всё слил?! Так ли это на самом деле? Или это минус общепринятой системы определения доходности?

Вся беда в том, что общественность определяет лишь «цену пая» каждого инвестора, а не реальную доходность, которую делает конкретный инвестор.

Элвис мне обещал прислать необходимые данные для расчета реальной доходности. Будет продолжение!

Источник