Кривая доходности и ее свойства
Если говорить простыми словами, то кривая доходности – это линия, показывающая изменение дохода от облигаций во времени. С ее помощью инвестор может легко определить, какие ценные бумаги – короткие или длинные – более доходны в данный момент. Ее также часто называют кривой бескупонной доходности или g-curve.
Но что такое доходность облигации? Она бывает разная. Согласно методике Московской биржи, используется сумма доходности к погашению, а также для некоторых выпусков рассчитываются корректирующие поправки. Обычно для кривой доходности используется параметры облигаций федерального займа, которые обладают максимальной надежностью и разнообразием. Читайте о них здесь. Однако кривую можно построить и по данным корпоративных облигаций.
Зачем нужна эта кривая инвесторам? По ней можно попробовать спрогнозировать, нормально ли будет развиваться экономика в ближайшее время. Как и на любой другой индикатор, на кривую бескупонной доходности не стоит полагаться безоговорочно — однако история показывает, что ее изменения предсказывают кризисы с очень неплохой точностью. К этому моменту мы еще вернемся.
Виды кривой доходности
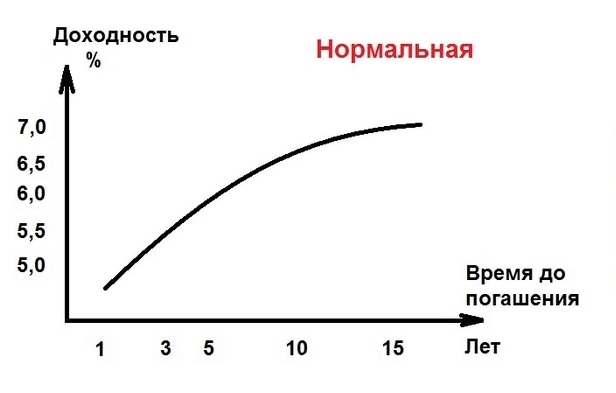
Итак, кривая доходности это графическая модель, показывающая, какой именно доход по облигациям получит держатель спустя определенный период времени. Обычно чем дольше срок погашения ценной бумаги, тем больше доход по ней. Срабатывает аналогия с банковским вкладом: чем больше срок размещения, тем выше процентная ставка, а значит, тем больше ожидаемая прибыль. Это нормальная ситуация, когда экономика не испытывает заметных проблем.
Но иногда линия может быть и перевернутой (инверсной) – т.е. чем дольше срок размещения, тем меньше доходность. Этот случай наблюдается в период серьезного кризиса, когда государство и участники рынка не могут надежно спрогнозировать экономическое развитие на ближайшие годы, так что текущая платежеспособность выходит на первый план. Переход от нормальной к инверсной модели обычно вызывает волнение рынка.
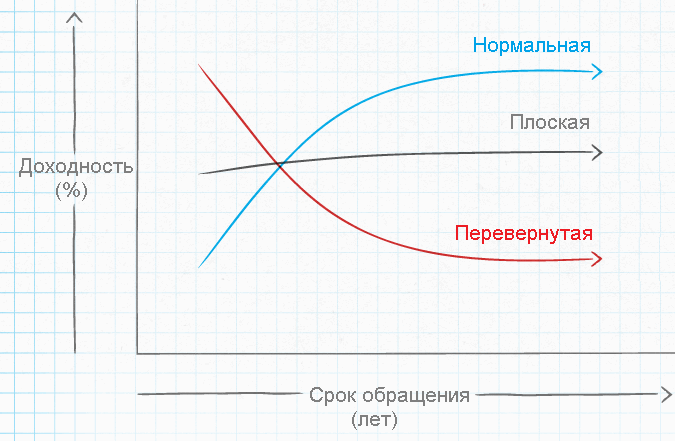
Кроме того, в некоторых случаях прибыль по облигациям не зависит от срока их размещения. Тогда кривая становится практически прямой – на практике ее называют плоской. Такая кривая может наблюдаться, к примеру, как переходное состояние между двумя случаями выше. Сравнение всех трех моделей представлено здесь:
Где можно посмотреть кривую?
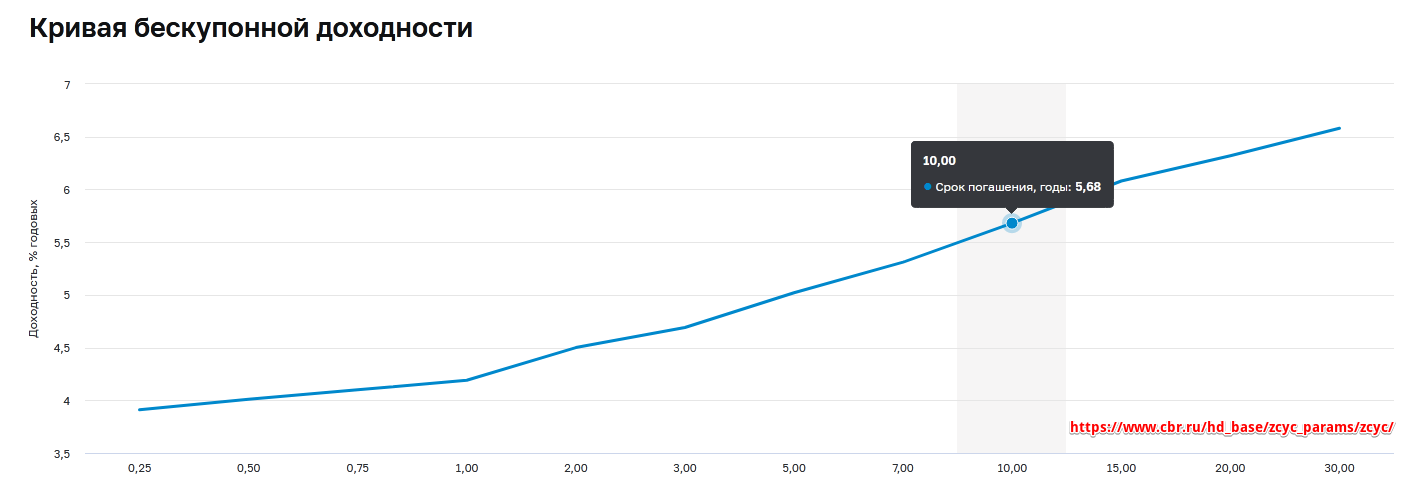
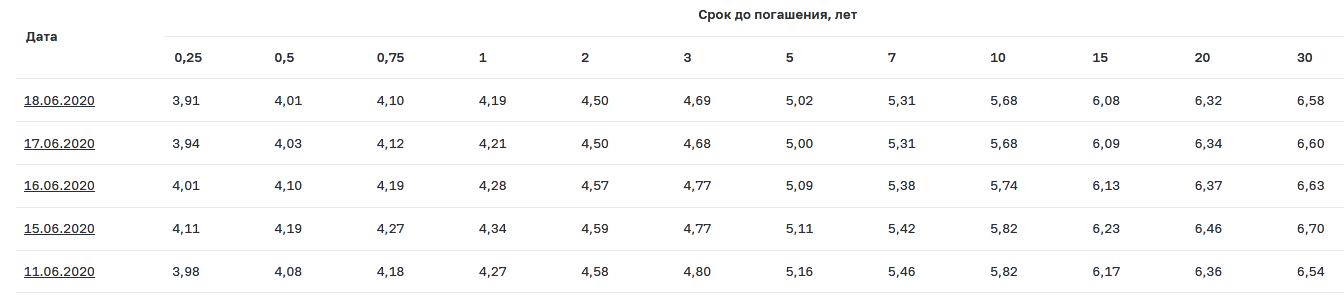
Кривая по данным ОФЗ публикуется в официальных источниках – на сайте Центрального Банка и Мосбиржи. Первый вариант:
Как видно, здесь представлены различные сроки обращения ОФЗ – от одного квартала до 30 лет. За каждый указанный период данные также представлены в табличном виде, причем все доходности пересчитываются каждый рабочий день.
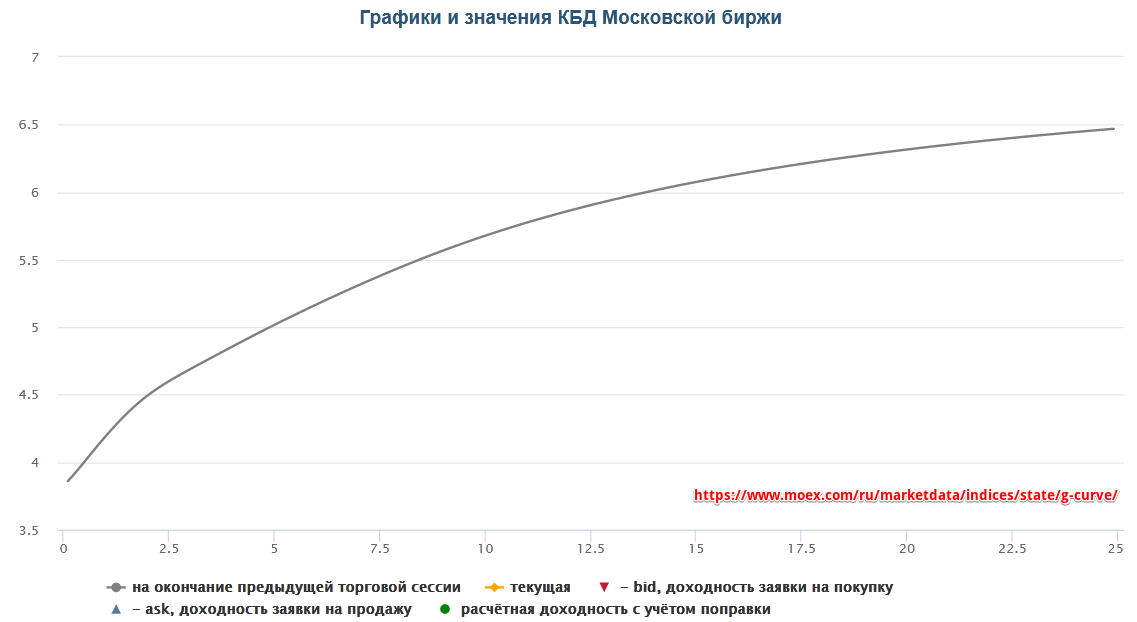
А вот так выглядит кривая бескупонной доходности (КБД) на сайте Московской биржи:
Итого, в обоих случаях представлена нормальная кривая доходности, что говорит о текущей стабильности рыночных настроений – несмотря на стартовавшее в феврале стремительное падение как американского, так и российского рынка. По указанным на графиках ссылкам или через поиск нетрудно найти на обоих сайтах актуальный вид кривой.

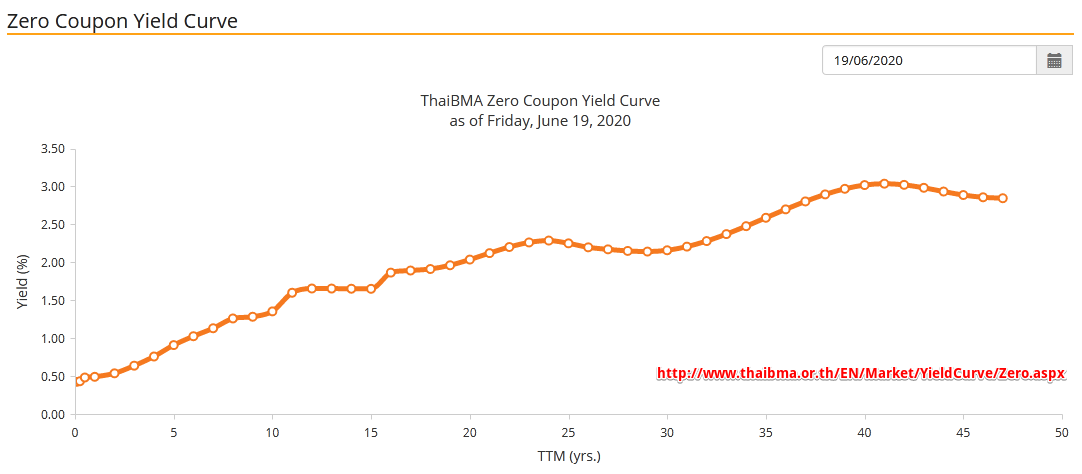
Теперь обратимся к США, где кривая Zero Coupon Yield Curve в данный момент также имеет вид, близкий к нормальному:
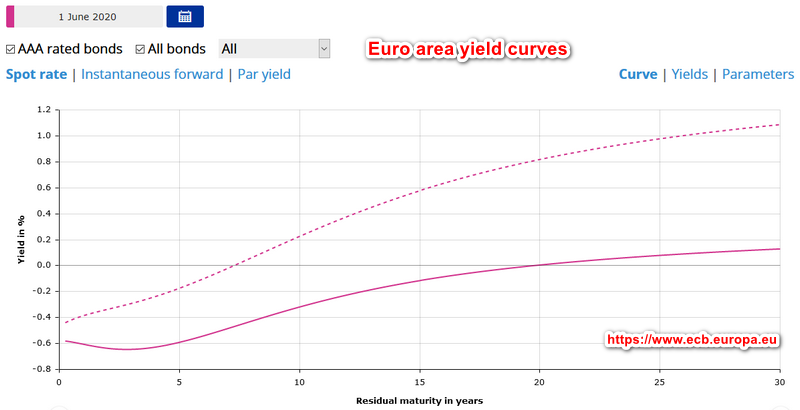
Актуальный график кривой доходности США тут . А вот в Европе ситуация ввиду отрицательных процентных ставок интереснее:
Здесь кривая AAA в начале пути получает небольшую «яму», в результате чего 3-х летние облигации с высшим рейтингом показывают наименьшую доходность. Затем она начинает расти, однако выходит в положительную зону лишь через 20 с лишним лет. Интересный вывод в том, что несмотря на вид кривой, близкий к нормальному, сами отрицательные доходности нормальными вряд ли являются. Пунктирная кривая показывает все виды гос. европейских облигаций, предлагая чуть больший доход. Актуальную кривую доходности смотрите здесь.
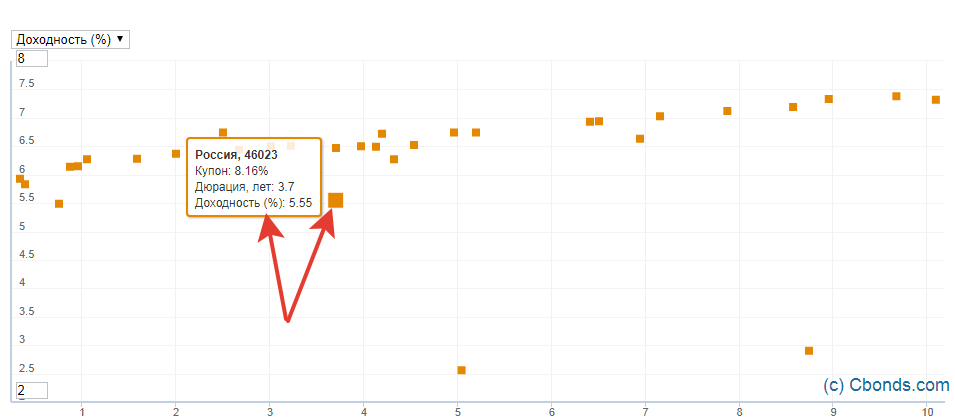
Построить линию можно и самостоятельно с помощью специальных программ или сайтов – например, терминала QUIK или сайта Cbonds. Преимуществом этого метода, в отличие от представленных выше, будет указание на графике названия облигаций. Инструкция по QUIK следующая:
- Зайти в программу
- Перейти во вкладку «Создать окно»
- Далее «Все типы окон» и F7
- Выбрать нужные облигации
- Построить график
От чего зависит кривая доходности?
Кривая доходности определяется доходностью ОФЗ, а она, в свою очередь, зависит от показателей ключевой ставки. Ключевая ставка периодически (несколько раз в год) устанавливается Центральным Банком России. По сути, это процент, под который ЦБ выдает кредиты коммерческим банкам. В настоящее время (июнь 2020 г.) она понижена до 4,5%. При этом еще на 1 января 2020 г. ставка равнялась 6,25%.
Известно, что рост ключевой ставки ведет к падению доходности облигаций. Это происходит потому, что новые выпуски будут платить купоны по новой (повышенной) процентной ставке и старую облигацию при прочих равных условиях (у нее ставка ниже) покупать будет просто невыгодно. Поэтому она ставится дешевле, обеспечивая новым инвесторам повышенный доход. Верны и обратные рассуждения, когда падение ключевой ставки повышает цену старых выпусков. Такая ситуация была на рынке российских облигаций в 2015-2020 году.
Также кривая доходности зависит от типа самих облигаций. Как показано выше, доходность по государственным ОФЗ на текущий момент составляет в среднем 5,0-6,5%. Это сопоставимо с банковскими депозитами (6,5% по ним можно считать очень хорошей ставкой). Однако есть и более доходные ценные бумаги – это корпоративные облигации. Относительно небольшие российские компании могут предложить по ним повышенный относительно ОФЗ доход.
Риски для инвестора
Глядя на нынешнее состояние кривой в России и США, довольно типичное для рынка в целом, кажется очевидным преимущество долгосрочных выпусков, которые дают максимальную доходность. Купил — и готово. Почему на практике все не так просто?
- Долгосрочные выпуски по отдельным бумагам составляют не менее 30 лет, что укладывается в инвестиционный горизонт далеко не каждого инвестора. Разумеется, рыночную ликвидную бумагу можно продать в любое время, но доход по ней в этом случае будет непредсказуемым. Цикл повышения ставок либо кризисы могут загнать котировки бумаги глубоко вниз;
- Возможность дефолта эмитента. Она не так велика даже для российских и особенно для американских государственных бумаг, однако история показывает, что дефолты различных государств случались в среднем раз в 40 лет. Так что на длинных дистанциях риски возрастают;
- Девальвация. Она не обязательно вызывает существенный рост цен на внутренние товары, но поездка за границу станет дороже и в этом смысле накопления от долгосрочных облигаций в национальной валюте могут выйти боком;
- Наконец, главный враг долгосрочных выпусков это инфляция и повышение ставки. Расчеты показывают, что даже если купон по облигациям будет на 1% превосходить инфляцию, покупательная способность будущей прибыли за 30 лет упадет более, чем в три раза.
Предсказание кризисов по кривой доходности
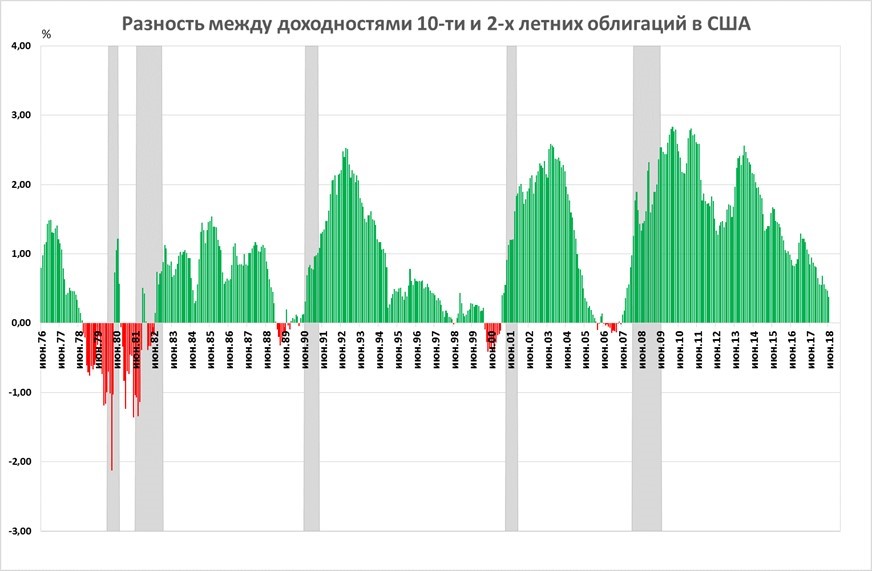
Возьмем для сравнения две облигации с достаточно коротким и достаточно длинным периодом: пусть это будут 2-х летние и 10-летние облигации. Как было сказано выше, в нормальном случае разница между доходом 10-летнего и 2-х летнего выпуска будет положительной, в случае инверсной кривой — отрицательной. Как выглядел исторически этот показатель для рынка США?
Здесь видно, что уход разницы ставок в отрицательную область неизбежно через год-полтора приводил к кризису на рынке (сильному падению акций). Интересно, что таким образом были предсказаны разные типы кризисов: такой, как пузырь доткомов 2000 года с переоценкой акций, и кризис недвижимости 2008 года, когда фундаментальные оценки акций были на обычном уровне.
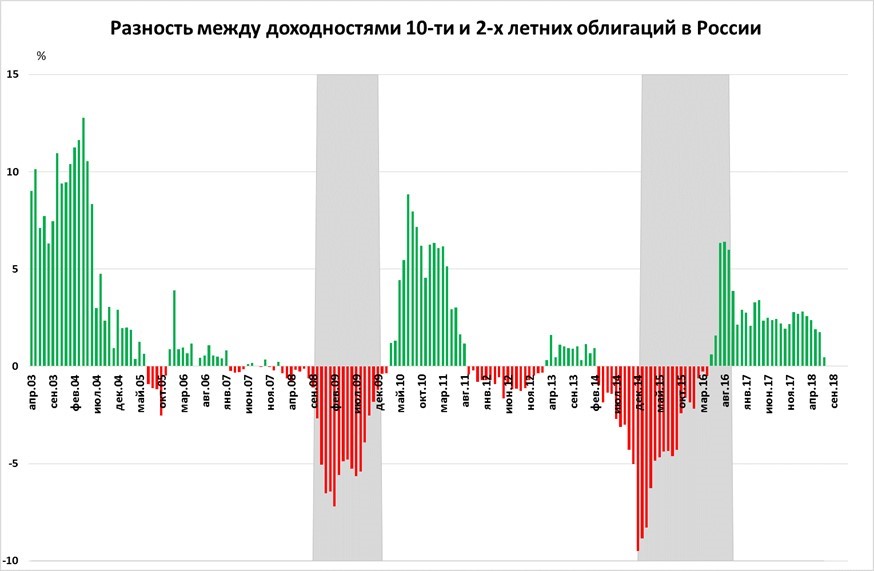
А теперь посмотрим, что было в России:
В России даже за заметно более короткий период времени видны «фальшивые» срабатывания в 2005 и в 2011 году, когда наблюдался лишь кратковременный спад без нового кризиса. Кроме того, видна более сильная волатильность, когда отрицательные показатели достигали заметных величин. Вывод? Не стоит переоценивать показатель, хотя исторически положительная разница и в России, и в США говорила о том, что в ближайшие месяцы рецессии ожидать не стоит.
Источник
Кривые рыночных доходностей
Рассмотрим некоторую купонную облигацию. Каждый отдельный купонный платеж и каждую выплату номинальной стоимости можно интерпретировать как облигацию с нулевым купоном при соответствующем сроке до погашения. В этом случае саму облигацию можно рассматривать как портфель облигаций с нулевыми купонами.
Так как купонная облигация и портфель соответствующих облигаций с нулевыми купонами характеризуются одинаковыми потоками платежей, то должны совпадать и их цены. Следовательно, зная внутренние доходности облигаций с нулевыми купонами, можно найти цену купонной облигации.
Набор внутренних доходностей облигаций с нулевыми купонами, выпущенных эмитентами одного и того же кредитного рейтинга, называют временной структурой процентных ставок (term structure of interest rates).
Графическое изображение временной структуры процентных ставок принято называть кривой (рыночных) доходностей (yield curve, zero coupon curve).
Кривая доходностей может изменяться с течением времени. На рис. 1-4 показаны примеры кривых рыночных доходностей.
Кривую рыночных доходностей для казначейских (государственных) облигаций называют кривой спот-ставок (spot curve).
Если известна кривая спот-ставок, то можно определить цену любой купонной казначейской облигации.
Рис. 1. Нормальный вид кривой доходностей
Рис. 2. Инверсный вид кривой доходностей
Рис. 3. Горбатый вид кривой доходностей
Рис. 4. Ровный вид кривой доходностей
Например, котируемая цена казначейских облигаций с полугодовыми купонами может быть найдена по следующей формуле (1):

А – номинальная стоимость облигации;
n – число купонных платежей, остающихся до погашения облигации;
ri – спот-ставка на i полугодовых периодов, i = 1, 2…., n.
Пример 1. Дана 8 %-ная казначейская облигация с полугодовыми купонами номиналом 100 долл. Определим цену этой облигации, когда до ее погашения остается 2 года, а спот-ставки на 0,5, 1,0, 1,5 и 2 года соответственно равны 6, 6,5, 6,8 и 7 %.
Согласно формуле (1), имеем:
Чтобы построить кривую спот-ставок, необходимо знать рыночные цены облигаций с нулевыми купонами при различных сроках до погашения. Однако обычно облигации с нулевыми купонами выпускаются лишь при небольших сроках до погашения. В таком случае кривую спот-ставок можно смоделировать на основе цен купонных облигаций с разными сроками до погашения.
Пример 2. На рынке имеются казначейские облигации с полугодовыми купонами номиналом 100 долл. со следующими данными:

1. 6-месячную спот-ставку можно найти с помощью первой облигации. Так как должно выполняться равенство

2. Спот-ставку на год можно определить по второй облигации из нашего списка:

3. Спот-ставку на 1,5 года будем искать с помощью третьей облигации, зная уже найденные спот-ставки r1 и r2.
Так как цена облигации должна совпадать с приведенной стоимостью потока платежей от этой облигации, то

4. Спот-ставку r4 найдем с помощью линейной интерполяции:

т. е. мы имеем уравнение с одним неизвестным. Решив это уравнение методом проб и ошибок, получим, что r5 = 0,0948. Тогда

В данном случае кривая спот-ставок имеет нормальный вид (рис. 5).
Рис. 5. Кривая спот-ставок из примера 2
В развитых финансовых системах государственные облигации считаются безрисковыми, а все остальные облигации принято с ними сравнивать. Для сравнения облигаций, выпущенных негосударственными эмитентами, с государственными облигациями можно использовать показатель, называемый спредом нулевой волатильности.
Спредом нулевой волатильности (zero-volatility spread) называют такую надбавку к спот-ставкам, при которой приведенная стоимость потока платежей от облигации совпадает с ее рыночной ценой.
Спред нулевой волатильности удовлетворяет следующему уравнению:

q – полугодовой купонный платеж;
А – номинальная стоимость облигации;
n – число купонных платежей, остающихся до погашения облигации;
ri – спот-ставка на i полугодовых периодов, i = 1, 2, …, n.
Источник