Как рассчитать дивидендную и полную доходность акции: формулы и коэффициенты
Инвестпривет, друзья! Доходность акций на фондовом рынке формируется за счет двух составляющих. Первая – это рост курсовой стоимости ценной бумаги. Вторая – дивиденды. Если у компании всё хорошо, то ее финансовые показатели повышаются, дивиденды увеличиваются и, как следствие, курс акций тоже растет. Давайте разбираться, чем виды доходности акций отличаются друг от друга, как их рассчитывать и как платить налоги.
Доходность акций на фондовом рынке
Итак, инвестор получает доход с акций двумя способами: за счет роста стоимости акции и за счет получаемых дивидендов.
В конце 19 – начале 20 века основным доходом на фондовой бирже считались дивиденды. Инвесторы скупали акции как раз для получения стабильного денежного потока. Компании стремились нарастить дивидендные выплаты, и именно их размер считался основной «пузомеркой» акционерного общества.
Однако после Великой Депрессии ситуация изменилась. Многие компании отказались от практики выплаты дивидендов. Вместо этого они сфокусировались на удержании прибыли внутри компании (а дивиденды – это как раз часть прибыли) и реинвестировании своих доходов в собственный бизнес.
За счет реинвеста прибыли росли показатели компании – в результате акции дорожали. Сейчас рост курсовой стоимости акции считается основным доходом инвестора на бирже, а дивиденды – приятным дополнением к общей прибыли.
Есть компании, которые вообще не выплачивают дивиденды, но которые очень хорошо растут. Хрестоматийные примеры – акции Google (Alphabet), Facebook, Tesla, Berkshire Hathaway, в России – Яндекс, Лента, Русал, М.Видео. В основном – это активно развивающиеся компании, которые вкладывают свои деньги в собственное развитие, новые разработки, покупку стартапов и т.д. Словом, руководству есть куда потратить прибыль, чем просто распределять ее между акционерами.
Но это свойственно только для зрелых рынков (типа США, Британии, Германии, Японии). На развивающихся рынках (например, России, Индии и Китая) дивидендная доходность акции продолжает играть главенствующую роль при определении котировок. Если компания не платит дивиденды, сокращает их или меняет политику выплат, то ее котировки падают. Если выплаты увеличиваются – котировки растут. Это одна из ключевых особенностей фондового рынка России.
Следовательно, на развивающихся рынках цена и доходность акций связаны и зависят друг от друга. Чем выше ожидаемая доходность акции, тем дороже стоит ценная бумага. Компании, которые на российском фондовом рынке стабильно платят дивиденды, увеличивая их размер, дорожают. Их немного, но они есть, например, Лукойл, Сбербанк, Татнефть.
Средняя доходность акций на разных рынках, понятное дело, будет разной. В США, например, дивидендная доходность акций в среднем равна 2-3% годовых. В тоже время в России этот показатель равен 7-9% годовых, и это один из самых больших показателей в мире.
Среднюю доходность акций конкретного рынка можно оценить, исходя их роста индекса. На сколько вырос индекс, на столько в среднем по больнице выросли акции. Но это очень грубая оценка. Если индекс вырос на 40%, это не говорит, что все акции в нем возросли на это значение. Какие-то акции могут вырасти на 60%, какие-то – всего на 10%, а какие-то и вовсе могут упасть.
Поэтому нет понятия «средняя доходность акций» – в каждом случае нужно смотреть индивидуально.
Таким образом, итоговая доходность акций складывается их двух составляющих:
- роста курсовой стоимости;
- дивидендов.
Доходность выражается в процентах или номинальном значении. Например, если акция стоила 200 рублей, а через год – 224 рубля, то говорят, что ее доходность составила 12% годовых или 24 рубля за год.
В ходе инвестирования можно получить и отрицательную доходность, если курсовая стоимость акции в итоге оказалась меньше начальной. Даже наличие дивидендов не всегда нивелирует убыток.
Например, акция на момент покупки стоила 850 рублей, на момент продажи – 600, были получены дивиденды в размере 50 рублей. В итоге доходность составит –18,75%.
Дивидендная доходность
Компания может платить дивиденды раз в год, полгода, квартал или даже ежемесячно. Решение о выплате дивидендов принимает Совет директоров, а утверждает их собрание акционеров. Чтобы получить дивиденды, нужно владеть акциями на день отсечки – т.е. последний день, когда они выплачиваются.
Дивидендная доходность акций определяется как отношение размера перечисленного дивиденда к курсу акции на конкретную дату. Есть несколько дат, относительно которых рассчитывают дивиденды (т.е. в этот день смотрят на цену акции):
- начало года;
- конец года;
- дата отсечки;
- дата составления аналитики / обзора (т.е. аналитик показывает текущую дивидендную доходность, как если бы вы купили акции прямо в момент составления обзора).
Иногда высчитывают средневзвешенную цену акции в течение года и высчитывают дивидендную доходность относительно этого значения – но это путь извращенцев 🙂
Понятно, что значение дивдоходности – динамическое. Размер объявленных дивидендов остается таким же, но котировки самой акции меняются буквально ежесекундно.
Поэтому дивидендная доходность меняется каждый день, и если вы где-то вычитали о высокой дивдоходности акции – перепроверьте данные. Возможно, цена уже «подтянулась», и ваша сделка окажется не такой выгодной.
По умолчанию дивидендная доходность рассчитывается как отношение размера дивиденда к курсу акций на дату отсечки. Если вы видите в каком-нибудь аналитическом материале дивидендный доход по акции – то расчет, скорее всего, делался на дату отсечки.
Формула расчета дивдоходности акции такова:
- r = d / p * 100, где
- d – размер дивиденда;
- p – текущая цена акции.
Например, за 2018 год Газпром выплатил 16,61 рублей на акцию. Дата отсечки – 18.07.2019. В тот день акции стоили 238,01 рубль. Дивидендная доходность – 6,97%.
Как я писал выше, дивиденды бывают годовые, полугодовые, квартальные (промежуточные) или ежемесячные. Если компания платит дивиденды за квартал, то рассчитываемая дивидендная доходность тоже будет квартальной. Чтобы рассчитать годовую дивидендную доходность, нужно сложить все дивиденды за год и разделить их на цену акции в день последней выплаты.
Как я уже писал, дивидендная доходность российских акций составляет в среднем от 7% до 12% годовых.
Рыночная доходность акций
Доходность, получившаяся за счет роста курсовой стоимости, рассчитывается по такой формуле:
- P1 – это цена покупки акции,
- Р2 – цена продажи акции.
Источник
Расчет рыночной доходности
Формула расчета рыночной доходности
Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.
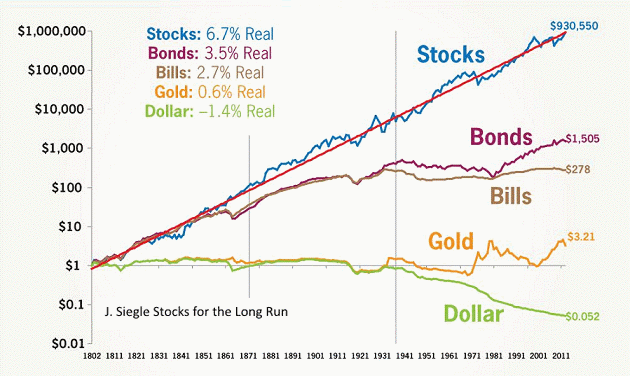
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):
Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.
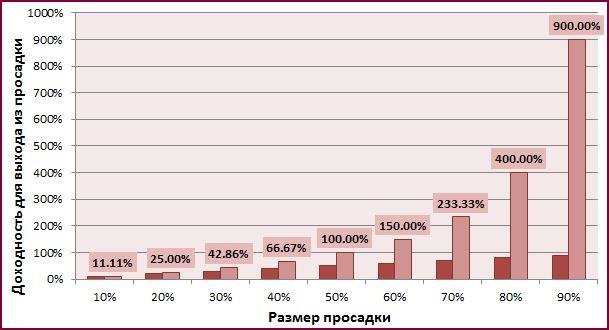
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть . К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:
Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.
В общем случае формула доходности выглядит так:
A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1
- A(0) – исходное количество денег
- А(n) – количество денег через n лет
- X – годовая доходность (в процентах)
Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то
A(n) = A(n-1) × Y = A(0) × Y^n
Задача
Актив растет на 10% в год. Какова будет его доходность через 2 года?
Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу
А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)
Обратная задача
Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):
Снова принимая нашу первоначальную доходность за условную единицу, считаем:
Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%
Задача 2
За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?
Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%
Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).
Задача 3
За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?
2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда
Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%
Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.
Задача 4
Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?
Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%
Задача 5
Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.
2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%
Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:
1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)
И средняя инфляция
Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%
P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.
Задача 6
Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?
Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.
Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.
Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).
Задача 7
Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.
Y = [(7.2 + (135-120))/120] × 100% = 18.5%
Задача 8
По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:
Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%
Источник