Решение задачи оптимизации инвестиций

Содержание

Задачи оптимизации инвестиций
Примеры решений задач по инвестированию
Задачи по инвестициям с решениями
Задачи оптимизации инвестиций
Постановка и решение задачи оптимального распределения инвестиций

Задачи оптимизации инвестиций

Основная цель решения этого класса задач — найти оптимальное ] распределение (вложение) финансовых средств, доставляющее максимальную прибыль (в будущем) по истечении срока действия инвестиционного проекта. Для этих задач характерно наличие большого раз- j нообразия способов вложения средств, использование ограничений в виде равенств, определяющих разделение общей суммы инвестиционных вложений на части — вложения в различные проекты. Число та-ких ограничений зависит от сроков реализации инвестиционных про-ектов. При этом на каждом временном отрезке, связанном с инвестициями, в электронной таблице «появляются» новые варьируемые] переменные. Такие переменные определяют процесс деления прибыли, полученной на предыдущем этапе инвестиций, на части — вложе-ния в проекты на последующем этапе.

При большом выборе инвестиционных проектов с различными сроками окупаемости и коэффициентами прибыли эти задачи стано-вятся весьма сложными и трудно формализуемыми.

Оптимизация инвестиций в проекты

Денежные средства могут быть использованы для финансирова-ния двух проектов. Проект А гарантирует получение прибыли в раз-мере 70 центов на вложенный доллар через год. Проект В гарантирует получение прибыли в размере 2 долл. на каждый инвестированный доллар, но через два года. При финансировании проекта В период инвестиций должен быть кратным двум годам. Как следует распоря-диться капиталом в 100 тыс. долл., чтобы максимизировать суммар-ную величину прибыли, которую можно получить через три года по-сле начала инвестиций?

Математическая формулировка задачи

Содержимое изменяемых ячеек

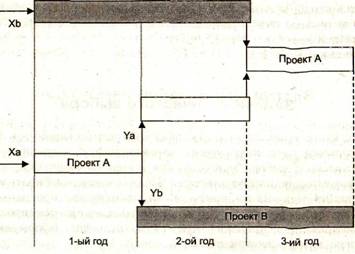
Ха, Ya — вложения в проект A; Xb, Yb — вложения в проекг В. Возможные инвестиции могут быть иллюстрированы схемой, приведенной на рисунке.

В этой схеме стрелки определяют возможные вложения в проекты, а символические обозначения на стрелках — объемы таких вложений. Из приведенной схемы следует, что в исследуемой системе существуют только два возможных срока вложений — начало первого года и начало второго года. Суммы вложений в эти сроки определяют содержимое изменяемых ячеек. «Точка вложений» в начале третьего года одна, в нее вкладываются все доходы от предыдущих вложений. Эта точка не связана с какими-либо вариациями сумм.

Ограничения: Ха + ХЬ = 100 000; Ya + Yb = (1 + 0.7)*Ха.

Целевая функция: Z = Ya*(l + 0.7) 2 + Yb*(l + 2) + Xb*(l + 2)*(1 + 0,7).

Представление этой задачи в форме электронной таблицы целесообразно оформить в следующем виде.

Часть 1. Поиск решений на электронных таблицах

Источник

Примеры решений задач по инвестированию

В этом разделе вы найдете решенные задачи по предмету «Инвестиции» (инвестирование, инвестиционный менеджмент и т.д.). Примеры решений выложены бесплатно для вашего удобства. Если вам нужна помощь в выполнении своих работ, оставьте заявку.

Задачи по инвестициям с решениями

Задача 1. Проект А имеет капитальные вложения в 65000 руб., а ожидаемые чистые денежные поступления составляют 15000 руб. в год в течение 8 лет.
а) Какой период окупаемости этого проекта?
б) Альтернативная доходность равна 14%. Какова чистая приведенная стоимость?
в) Внутренняя норма доходности?
г) Индекс доходности?

Задача 2. а) Каковы периоды окупаемости каждого из следующих проектов (данные в таблице)
б) При условии, что вы хотите использовать метод окупаемости, и период окупаемости равен двум годам, на какой из проектов вы согласитесь?
в) Если период окупаемости равен трём годам, какой из проектов вы выберете?
г) Если альтернативные издержки составляют 10 %, какие проекты будут иметь положительные чистые текущие стоимости?
д) «В методе окупаемости слишком большое значение уделяется потокам денежных средств, возникающим за пределами периода окупаемости». Верно ли это утверждение?
е) «Если фирма использует один период окупаемости для всех проектов, вероятно, она одобрит слишком много краткосрочных проектов». Верно, или неверно?

Задача 3. Компания должна выбрать одну из двух машин, которые выполняют одни и те же операции, но имеют различный срок службы. Затраты на приобретение и эксплуатацию машин приведены в таблице.
(а) Какую машину следует купить компании, если ставка дисконта равна 6 %?
(б) Предположим, что вы финансовый менеджер компании. Если вы приобрели ту или другую машину и отдали её в аренду управляющему производством на весь срок службы машины, какую арендную плату вы можете назначить.
(в) Обычно арендная плата, описанная в вопросе (б), устанавливается предположительно — на основе расчёта и интерпретации равномерных годовых затрат. Предположим, вы действительно купили одну из машин и отдали её в аренду управляющему производством. Какую ежегодную арендную плату вы можете устанавливать на будущее, если темп инфляции составляет 8 % в год? (Замечание: арендная плата, рассчитанная в вопросе (а), представляет собой реальные потоки денежных средств. Вы должны скорректировать величину арендной платы с учётом инфляции).

Задача 4. Имеются следующие условные данные по двум вариантам проекта (табл. 1)
Требуется:
1. Определить по вариантам чистый дисконтированный доход (ЧДД), индекс доходности (ИД) и срок окупаемости (Т_ок).
2. Найти лучший вариант проекта.
За момент приведения к расчетным ценам принят конец 2-го года.

Задача 5. Выбрать наиболее эффективный инвестиционный проект при норме прибыли r =15% и следующих условиях: Проект Инвестиции 1С Прибыль по годам (Р) у.е.
Р1 Р2 Р3 Р4
П1 300 90 100 120 150
П2 300 150 120 100 90
Определить: NPV, PI, IRR

Задача 6. Рассчитать внутреннюю норму доходности проекта «Заря» стоимостью 180 млн. руб., если он в течение 7 лет обеспечивает ежегодный доход 35 млн. руб.

Задача 7. Компания Игрек анализирует ожидаемые денежные потоки двух альтернативных проектов (в тыс. руб):
Год 0 1 2 3 4 5 6 7
А -300 -387 -192 -100 600 600 850 -180
В -405 134 134 134 134 134 134 0
Рассчитать внутреннюю норму доходности каждого проекта.

Читайте также: Чиа рецепты с клубникой

Задача 8. Проектом предусмотрено приобретение машин и оборудования на сумму 150000 у.е.. Инвестиции осуществляются равными частями в течение двух лет. Расходы на оплату труда составляют 50000 у.е., материалы – 25000 у.е.. Предполагаемые доходы ожидаются во второй год в объеме 75000 у.е., третий — 80000 у.е., четвертый — 85000 у.е., пятый — 90000 у.е., шестой — 95000 у.е., седьмой — 100000 у.е. Оцените целесообразность проекта при цене капитала 12% и если это необходимо предложите меры по его улучшению.

Источник

Задачи оптимизации инвестиций

Оптимизация инвестиций в проекты

Математическая формулировка задачи

Содержимое изменяемых ячеек

Ограничения: Ха + ХЬ = 100 000; Ya + Yb = (1 + 0.7)*Ха.

Целевая функция: Z = Ya*(l + 0.7) 2 + Yb*(l + 2) + Xb*(l + 2)*(1 + 0,7).

Представление этой задачи в форме электронной таблицы целесообразно оформить в следующем виде.

Часть 1. Поиск решений на электронных таблицах

Примеры структуризации задач

Изменяемые ячейки: СЗ:С4, ЕЗ:Е4. В двух первых размещаются вложения первого года, в двух последних — вложения второго года. Ограничения: С5 = Н6; Е5 = D5; Целевая ячейка: Н5.

Источник

Постановка и решение задачи оптимального распределения инвестиций

Экономическая эффективность капитальных вложений (инвестиций) — одна из важнейших проблем планирования, характеризующая целесообразность вложений финансовых и других средств.

Рационального распределения инвестиций можно достигнуть лишь на основе тщательных экономических расчетов, дающих возможность определить пути достижения максимальной отдачи, т.е.

При установлении структуры инвестиций на государственном уровне необходимо исходить из предусмотренных темпов развития отраслей экономики страны, обеспеченности их основными фондами и степени использования мощностей, объема сырья и материалов, поступающих из смежных отраслей, и ряда других факторов.

Межотраслевое распределение инвестиций должно сопровождаться распределением вложений внутри отрасли и, в частности, между предприятиями, выпускающими однородную продукцию. Критерием для оптимального распределения инвестиций могут служить максимальная прибыль, максимальный суммарный прирост продукции, максимальное снижение себестоимости, максимальная занятость населения и т.п.

Задача оптимального распределения инвестиций по своей природе комбинаторная. Например, при определении фондоотдачи от 10 млрд руб. в четыре отрасли промышленности необходимо перебрать все распределения числа 10 на четыре группы. При условии распределения только из целых чисел необходимо подсчитать 286 комбинаций:

(10, 0, 0, 0); (9, 1, 0, 0); (9, 0, 1, 0); (9, 0, 0, 1) . ;

(8, 1, 1, 0); (8, 1, 0, 1); (8, 0, 1, 1); (8, 2, 0, 0); (8, 0, 2, 0); (8, 0, 0, 2);

(4, 3, 2, 1); . (4, 2, 2, 2); .

Если требуется дополнительно определить оптимальное решение задачи в случае, когда инвестиции в целом составляют 9, 8, 7, . 1 млрд руб., то необходимо провести большой объем вычислительной работы.

Метод динамического программирования позволяет находить оптимальное решение задач по распределению однородных средств между объектами при значительно меньшем, по сравнению с комбинаторным способом решения, объеме вычислительной работы.

В общем виде математическая постановка задач по распределению однородных средств (капитальных вложений, машин, сырья и т.д.) между объектами формулируется следующим образом: найти значения неизвестных xv х2, . х, . хп, т.е. план распределения, удовлетворяющий условиям:

обращающие в максимум функцию

(4.2)

где— сумма возможных вложений по j-му объекту (отрасль, предприятие, цех, участок);

— фондоотдача по предполагаемому j-му объекту, т.е. функция отдачи капитальных вложений (прибыль, прирост продукции и т.д.).

Алгоритм, предложенный Беллманом, справедлив для функцийлюбого вида и является одним из простейших примеров применения динамического программирования. Идея алгоритма состоит в том, что последовательно решаются задачи оптимального распределения средств между первыми j объектами (здесь j принимает значения 1, 2, 3, . n). Последняя из этих задач является решением поставленной.

В задаче по распределению средств между объектами всегда предполагаются известными значения функций f.(x) при всех возможных значениях аргументов (табл. 4.7).

Источник