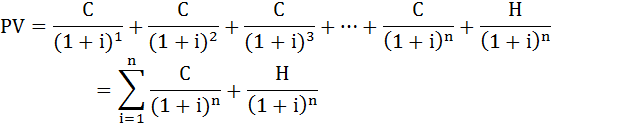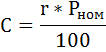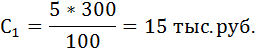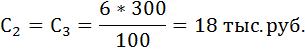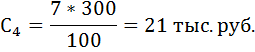Решение задач по облигациям инвестиции

Примеры задач по ценным бумагам

В этом разделе вы найдете решенные задачи по предмету «Ценные бумаги». Примеры решений выложены бесплатно для вашего удобства. Если вам нужна помощь в выполнении своих работ по рынку ценных бумаг, оставьте заявку. Еще примеры работ — на странице Готовые контрольные: РЦБ.

Задачи с решениями по рынку ценных бумаг

Задача 1. (а) Вычислите приведенные стоимости каждой из следующих облигаций при допущении, что доходность к погашению равна 8 %, а номинальная стоимость 1000 руб. (данные в таблице).
(б) Пересчитайте приведенную стоимость облигаций при условии, что доходность к погашению равна 10 %.
(в) Увеличение требуемой инвесторами доходности имеет большее влияние на цены долгосрочных или краткосрочных облигаций?

Задача 2. Корпоративные облигации можно эмитировать по номиналу, со скидкой или с премией. Компания намерена эмитировать новые 10-летние облигации. Ставка дисконтирования для этих облигаций равна 15%.
(а) Какой должна быть купонная ставка, чтобы можно было эмитировать эти облигации по номиналу?
(б) Если номинал облигации равен 1000 руб., а купонная ставка — 10%, то какова теоретическая стоимость этих облигаций?

Задача 3. Вы имеете облигации с нулевым купоном, номиналом 1000 руб. и сроком погашения через 10 лет. Найдите их приведенную стоимость при дисконтировании будущих платежей под 10% годовых: (а) при начислении процентов каждые полгода; (б) при ежегодном начислении процентов.

Задача 4. Ожидается, что компания X в конце года выплатит дивиденды в размере 10 руб. на акцию и что после выплаты дивидендов акция будет продана за 110 руб. Если ставка рыночной капитализации равна 10 %, то по какой цене её можно купить в данный момент?

Задача 5. Компания Y не реинвестирует прибыли, и предполагается, что дивиденды составят 5 руб. на привилегированную акцию. Если в настоящее время цена акции равна 40 руб., какова ставка рыночной капитализации?

Источник

Примеры решений задач по инвестированию

В этом разделе вы найдете решенные задачи по предмету «Инвестиции» (инвестирование, инвестиционный менеджмент и т.д.). Примеры решений выложены бесплатно для вашего удобства. Если вам нужна помощь в выполнении своих работ, оставьте заявку.

Задачи по инвестициям с решениями

Задача 1. Проект А имеет капитальные вложения в 65000 руб., а ожидаемые чистые денежные поступления составляют 15000 руб. в год в течение 8 лет.
а) Какой период окупаемости этого проекта?
б) Альтернативная доходность равна 14%. Какова чистая приведенная стоимость?
в) Внутренняя норма доходности?
г) Индекс доходности?

Задача 2. а) Каковы периоды окупаемости каждого из следующих проектов (данные в таблице)
б) При условии, что вы хотите использовать метод окупаемости, и период окупаемости равен двум годам, на какой из проектов вы согласитесь?
в) Если период окупаемости равен трём годам, какой из проектов вы выберете?
г) Если альтернативные издержки составляют 10 %, какие проекты будут иметь положительные чистые текущие стоимости?
д) «В методе окупаемости слишком большое значение уделяется потокам денежных средств, возникающим за пределами периода окупаемости». Верно ли это утверждение?
е) «Если фирма использует один период окупаемости для всех проектов, вероятно, она одобрит слишком много краткосрочных проектов». Верно, или неверно?

Задача 3. Компания должна выбрать одну из двух машин, которые выполняют одни и те же операции, но имеют различный срок службы. Затраты на приобретение и эксплуатацию машин приведены в таблице.
(а) Какую машину следует купить компании, если ставка дисконта равна 6 %?
(б) Предположим, что вы финансовый менеджер компании. Если вы приобрели ту или другую машину и отдали её в аренду управляющему производством на весь срок службы машины, какую арендную плату вы можете назначить.
(в) Обычно арендная плата, описанная в вопросе (б), устанавливается предположительно — на основе расчёта и интерпретации равномерных годовых затрат. Предположим, вы действительно купили одну из машин и отдали её в аренду управляющему производством. Какую ежегодную арендную плату вы можете устанавливать на будущее, если темп инфляции составляет 8 % в год? (Замечание: арендная плата, рассчитанная в вопросе (а), представляет собой реальные потоки денежных средств. Вы должны скорректировать величину арендной платы с учётом инфляции).

Задача 4. Имеются следующие условные данные по двум вариантам проекта (табл. 1)
Требуется:
1. Определить по вариантам чистый дисконтированный доход (ЧДД), индекс доходности (ИД) и срок окупаемости (Т_ок).
2. Найти лучший вариант проекта.
За момент приведения к расчетным ценам принят конец 2-го года.

Задача 5. Выбрать наиболее эффективный инвестиционный проект при норме прибыли r =15% и следующих условиях: Проект Инвестиции 1С Прибыль по годам (Р) у.е.
Р1 Р2 Р3 Р4
П1 300 90 100 120 150
П2 300 150 120 100 90
Определить: NPV, PI, IRR

Задача 6. Рассчитать внутреннюю норму доходности проекта «Заря» стоимостью 180 млн. руб., если он в течение 7 лет обеспечивает ежегодный доход 35 млн. руб.

Задача 7. Компания Игрек анализирует ожидаемые денежные потоки двух альтернативных проектов (в тыс. руб):
Год 0 1 2 3 4 5 6 7
А -300 -387 -192 -100 600 600 850 -180
В -405 134 134 134 134 134 134 0
Рассчитать внутреннюю норму доходности каждого проекта.

Задача 8. Проектом предусмотрено приобретение машин и оборудования на сумму 150000 у.е.. Инвестиции осуществляются равными частями в течение двух лет. Расходы на оплату труда составляют 50000 у.е., материалы – 25000 у.е.. Предполагаемые доходы ожидаются во второй год в объеме 75000 у.е., третий — 80000 у.е., четвертый — 85000 у.е., пятый — 90000 у.е., шестой — 95000 у.е., седьмой — 100000 у.е. Оцените целесообразность проекта при цене капитала 12% и если это необходимо предложите меры по его улучшению.

Источник

Задача №20. Расчёт текущей стоимости облигации

Определить текущую стоимость муниципальной облигации из портфеля ценных бумаг коммерческого банка.

Номинальная стоимость облигации 300 тыс. руб.

До погашения четыре года.

Годовая ставка купонного дохода по облигации соответственно: 5%, 6%, 6%, 7%.

Рыночная процентная ставка – 8% в год.

Решение:

Текущую стоимость облигации можно определить как стоимость ожидаемого денежного потока, приведённого к текущему моменту времени. Денежный поток состоит из двух компонентов: купонных выплат и наминала облигации, выплачиваемого при её погашении. То есть, цена облигации будет равна приведённой стоимости аннуитета и единовременно выплачиваемой суммы номинальной стоимости.

Формула расчёта текущей стоимости облигации будет следующей:

C – купонные выплаты;

i – рыночная процентная ставка в период t (доходность в альтернативные финансовые инструменты);

H – номинальная стоимость облигации;

n – число периодов, в течении которых осуществляется выплата купонного дохода.

Рассчитаем купонные выплаты. Абсолютная величина годовой доходности рассчитывается по формуле:

r – годовая ставка купонного дохода по облигации, %;

Р_ном – номинальная стоимость облигации.

Купонная выплата за первый год:

Купонная выплата за второй и третий год:

Купонная выплата за четвёртый год:

Таким образом, текущая стоимость муниципальной облигации из портфеля ценных бумаг коммерческого банка будет равна:

Источник

Решение задач по облигациям инвестиции

Ориентиром доходности облигаций служит номинальная (нарицательная) цена бумаги, фиксируемая на бланке.

Р_н — номинальная цена бумаги,

З — сумма займа, приходящаяся на все долговые обязательства определенного достоинства

К — кол-во эмитируемых бумаг определенного достоинства.

Облигации эмитируются, как правило, с высокой номинальной ценой и ориентированы либо на богатых инвесторов, либо на институциональных инвесторов. Лица с относительно невысокими доходами могут приобрести облигации через инвестируемые фонды.

Эмиссионная цена— это цена первичного размещения. Она может быть больше, меньше, равной номинальной. Если эмиссионная цена меньше номинальной, то цена оказывается дисконтной или со скидкой. Если эмиссионная цена больше номинальной, то цена называется с премией.

Рыночная (курсовая) цена — это цена, по которой облигация продаётся на вторичном рынке. Отношение рыночной цены ( Р_р) к номинальной (Р_н), выраженной в %-тах называется курсом.

Доходность облигаций определяется двумя факторами:

1. вознаграждение за предоставляемый эмитенту заём — купонные выплаты,

2. разница между ценой по гашения и ценой приобретения ц.б.

1. Купонные выплаты выражаются абсолютной величиной или в %-тах:

I_к — купонный доход,

iд — купонная годовая %ая ставка.

Облигация может быть реализована не в начале фин-ого года. Тогда купонный доход будет делиться между прежним и новым владельцем.

t₁ — число дней от даты продажи до очередного %-ого дня (даты выплаты по купону),

t₂ — число дней от прошедшего процентного дня до даты продажи.

На основании годового купонного дохода определяется купонная (текущая) доходность — ставка текущего дохода.

Р_пр — цена приобретения облигации

2. Разница между ценой приобретения погашения бумаги определяет величину прироста или убытка капитала за весь срок займа .

ДельтаР = Р_н — Р_д, ДельтаР›0 (прирост капитала)

ДельтаР = Р_н -Р_премия, ДельтаР‹0 (убыток капитала)

Р_д — цена со скидкой (дисконтом)

Р_премия — цена с премией

n -число лет займа

Годовой совокупный доход

Совокупная доходность (ставка совокупного дохода, ставка помещения)

Совокупный доход за весь срок займа

Совокупная доходность за весь срок займа

1 Облигация приобретена по курсовой цене 1200 рублей, погашается через 5 лет по номиналу 1000 рублей. Купонная ставка равна 8%. Определить ставку помещения по данной бумаге.

1000-1200 = -200 (убыток капитала)

-200/5 = — 40 (годовой убыток капитала)

0,08*1000 = 80 (купонный доход)

(80+ (-40))/1200 = 0,033 или 3,3% (ставка помещения)

2 Облигация приобретена по курсовой цене 1300 рублей. Погашается через 3 года по номиналу 1000 рублей. Купонная ставка 20%. Определить ставку совокупного дохода по облигации за весь срок займа.

0,2*1000=200 (купонный доход)

(1000-1300)/3 =-100 (годовой убыток капитала)

(200-100) *3/1300 = 0,2308 или 23,08% (ставка помещения)

3. Облигация с номиналом 1000 рублей с 5%-ой купонной ставкой и погашением через 5 лет приобретена с дисконтом 10%. Определить текущую и совокупную доходность бумаги за год и за 5 лет.

1000*0,05 = 50 (купонный доход)

(1000-1000*(1-0,1))/5 = 20 (годовой прирост капитала)

(50+20)/900 = 0,078 (совокупная годовая доходность)

0,078*5 = 0,39 (совокупная доходность за 5 лет)

4. Облигация номиналом 10000 рублей и сроком займа 5 лет с ежегодной выплатой 50% приобретена с премией за 14000 рублей. В 1-ый, 2-ой, 3-ий, 4-ый и 5-ый год после эмиссии. Погашение проводится по номиналу. Определить годовой убыток капитала, годовой совокупный доход, годовую совокупную доходность для разных сроков приобретения облигаций.

(10000-14000)/5 = -800 (годовой убыток капитала для 5 лет)

(10000-14000)/4 = -1000 (годовой убыток капитала для 4 лет)…

Источник

Решение типовых задач

Параметры облигации

Дата аукциона или дата выплаты купона	Номер периода	Купонный дней	Величина, % в год	Размер объявленного купона, руб.
21.01.98 22.07.98	1	182	15	74,79
20.01.99	2	182	15	74,79
21.07.99	3	182	15	74,79
19.01.00	4	182	15	74,79
19.07.00	5	182	15	74,79
17.01.01	6	182	15	74,79

1. Находим «чистую» стоимость облигации:

Р = 1000 х 91,5/100 = 915 руб.

2. Рассчитываем накопленный купонный доход (НКД):

С1 = 1000 х 0,15 х (182/365) = 74,79 руб. (это размер купона; последний столбец табл.

11 = 19/07/00 — 26/04/00 = 84 дня (это количество дней до вы­платы ближайшего купона);

Т = 182 (дня купонный период);

НКД = (74,79/182) х (182 — 84) = 40,272 руб.;

Цена облигации с НКД («грязная» цена) = 915 + 40,272 = = 955,272 руб.

Параметры облигации

Задача 2. Определите приемлемый для вас максимальный курс по­купки государственной купонной облигации ОФЗ-ФД № 27001ИМР35 на вторичных торгах 26 апреля 2000 г., но при условии, что альтер­нативное вложение обладает доходностью 50% годовых. Номинал 10 руб. Параметры облигации указаны в табл. 6.2.

Дата аукциона или дата выплаты купона	Номер купонного периода	Купонный дней	Величина купона, в % год	Размер объявленного купона, руб.
19.08.98 10.02.99	1	175	30	1,44
12.05.99	2	91	30	0,75
11.08.99	3	91	30	0,75
10.11.99	4	91	25	0,62
09.02.00	5	91	25	0,62
10.05.00	6	91	25	0,62
09.08.00	7	91	25	0,62
08.11.00	8	91	20	0,50
07.02.01	9	91	20	0,50
09.05.01	10	91	20	0,50
08.08.01	11	91	20	0,50
07.11.01	12	91	15	0,37
06.02.02	13	91	15	0,37

Таблица 6.2

Размер купона в рублях уже рассчитан в последнем столбце

табл. 6.2. Произведем расчет «грязной» цены облигации исходя из

„ _ТТ77ТТ 0,62 0,62 0,50 0,50 0,50 0,50 0,37

Р + НКД = — 1 1 1 1 1 1 1

14 105 196 287 378 469 560

„ _365 , _г 365 , _365 , _г 365 , _365 , ^ 365 , ^ 365

1,5 1,5 1,5 1,5 1,5 1,5 1,5

Р + НКД = 7,783628153 руб.

Расчет НКД ОФЗ-ФД:

С = 10 х 0,25 х (91/365) = 0,62 руб. (размер купона; последний столбец табл. 6.2);

6 = 10/05/00 — 26/04/00 = 14 дней (количество дней до выплаты ближайшего купона);

Т = 91 день (купонный период);

НКД ОФЗ-ФД = (0,62/91) х (91 — 14) = 0,5246154 руб.;

Р = 7,783628153 — 0,5246154 = 7,259013 (руб.).

Приемлемый курс облигации: 72,59%.

Задача 3. На вторичных торгах 26 апреля 2000 г. курс ГКО № 21139ИМР39 составлял 98,68%, курс ОФЗ-ПД № 25021ИМР35 — 91,5%; курс ОФЗ-ФД № 27001ЯМР35 — 78,99%. Надо определить:

1) в какие ценные бумаги инвестиции будут наиболее эффек­тивными с точки зрения доходности к погашению (доходность рас­считать с учетом простой и сложной процентной ставки; данные по купонным облигациям следует взять из предыдущих задач; пара­метры ГКО № 21139ЯМР39: номинал 1000 руб.; погашение 31 мая 2000 г.);

2) текущую (фактическую) доходность для купонных облигаций при условии, что цены аукционов соответствующих облигаций составляют: ОФЗ-ПД № 25021 ЯМР35—80%; ОФЗ-ФД № 27001ЯМР35—70%.

1. Рассчитаем доходность к погашению по ГКО № 21139ИМР39, исходя из сложной и простой процентной ставки:

Р = 98,68 х 1000/100 = 986,8 руб.;

^погаш = 31/05/2000 — 26/04/2000 = 35 дней.

і = [(1000/986,8) — 1] х 365 х 100/35 = 13,95%. Сложная ставка:

» 365 ‘	‘ 365 «
( N 3 і	х 100% =	( 1000 3 35 ,
1 — 1 -1		1——- 1 -1
1Р )		1,986,8 )

X 100 = 14,8634 %.

2. Рассчитаем доходность к погашению по ОФЗ-ПД № 25021ИМР35, исходя из сложной и простой процентной ставки:

365

• 100%,

(N — P +£ Ск — НКД) P + НКД

где N = 1000 руб.;

Р = 91,5 х 1000/100 = 915 руб.;

С₁ = 1000 X 0,15 X (182/365) = 74,79 руб.;

?_погаш. = 84 + 182 = 266 дней.

/ = [(1000 — 915 + 74,79 х 2 -40,272)/955,272) х (365/266) х 100 = = (194,308/955,272) х 137,218 = 27,91%.

1 + ^l 365 ^1 + je «1 365

74,79 +1000

915 + 40,272 = £ Отсюда находим ie, при помощи стандартных средств Excel (функция «подбор параметров»). 3. Рассчитаем доходность к погашению по ОФЗ-ФД № 27001ИМЕ35, исходя из сложной и простой процентной ставки: X 365 х 100%, (N — P + XC. — НКД) P + НКД P = 10 х 78,99/100 = 7,899 руб.; C1 = 10 х 0,25 х (91/365) = 0,62 руб.; НКД = 0,5246154 руб.; ^огаш. = 14 + 7 х 91 = 651 день. i = [(10 — 7,899 + 2 х 0,62 + 4 х 0,5 + 0,37 х 2 — 0,5246154)/ /8,423615385] х (365/651) х 100 = [(10 — 7,899 + 1,24 + 2 + 0,74 — — 0,5246154)/ 8,423615385] х 56,067588325 = (5,5563846/8,423615385) х х 56,067588325 = 36, 983299%. Сложная ставка: расчет эффективной доходности к погашению (ie) при помощи стандартных средств Excel дал результат, равный 41,67% годовых. Таким образом, наибольшей доходностью обладают инвестиции в ОФЗ-ФД № 27001RMFS5. Данное обстоятельство легко объясни­мо, ведь чем больше срок инвестирования, тем больше должна быть доходность инвестиционного инструмента. 3 365 -100. 4. Рассчитаем текущую доходность купонных облигаций: P 2 + X K i + А 2 _ 1 P + A (915 + 4 X 74,79 + 40,272/ 365 100 692899% іпф3 пн = I !! I x x 100 = 69,2899%; офз -пд ^ 800 + 0 ) 826 ’ ’ ( 7,899 +1,44 + 0,75 x 2 + 0,62 x 2 + 0,5246154 3 365 . . . „ офз-Фд І 7 + 0 І 616 Задача 4. Есть две государственные облигации ОФЗ-ФД: серии 27001ЯМЕ35 и серии 27011ЯМЕ34. На вторичных торгах 26 апреля 2000 г. курс этих облигаций составлял 78,99 и 61,4% соответствен­но. Основные показатели ОФЗ-ФД № 27001ЯМЕ35 надо взять из предыдущих задач. Параметры ОФЗ-ФД № 27011ИМЕ34 указаны в табл. 1) найти среднерыночную доходность к погашению по пред­ставленным ценным бумагам; 2) определить дюрацию, модифицированную дюрацию и коэф­фициент Маколи (как изменится курс каждой облигации при изме­нении рыночночной доходности на 1%). Таблица 6.3 Параметры ОФЗ-ФД № 27011КМЕ84 Дата аукциона или выплаты купона Номер купонного периода Купонный период, дней Величина купона, % годовых Размер объявленного купона, руб. 1 2 3 4 5 19.08.98 14.07.99 1 329 30 2,7 13.10.99 2 91 25 0,62 12.01.00 3 91 25 0,62 Окончание табл. 6.3 1 2 3 4 5 12.04.00 4 91 25 0,62 12.07.00 5 91 25 0,62 11.10.00 6 91 20 0,5 10.01.01 7 91 20 0,5 11.04.01 8 91 20 0,5 11.07.01 9 91 20 0,5 10.10.01 10 91 15 0,37 09.01.02 11 91 15 0,37 10.04.02 12 91 15 0,37 10.07.02 13 91 15 0,37 09.10.02 14 91 10 0,25 08.01.03 15 91 10 0,25 09.04.03 16 91 10 0,25 09.07.03 17 91 10 0,25 08.10.03 18 91 10 0,25 1. Произведем расчет доходности к погашению по ОФЗ-ФД № 27011RMFS4: Ci = 10 х 0,25 х (91/365) = 0,62 руб. (размер купона; последний столбец табл. 6.3); 6 = 12/07/00—26/04/00 = 77 дней (количество дней до выплаты ближайшего купона); Т = 91 день (купонный период); НКД = (0,62/91) х (91 — 77) = 0,0953846 руб.; Цена облигации с НКД («грязная» цена) = «Чистая» цена + На­копленный купонный доход = 10 х 0,614 + 0,0953846 = 6,2353846 руб. (соответственно «грязный» курс = 6,24 х 100/10=62,4%); Расчет эффективной доходности к погашению (ie) при помощи стандартных средств Excel дал результат, равный 42,5% годовых. Эффективная доходность к погашению для ОФЗ-ФД № 27001RMFS5 равна 41,67% (задача 3, п. 3). 2. Рассчитаем среднерыночную процентную ставку: 3. Рассчитаем дюрацию и коэффициент Маколи для каждой об­лигации: D27011RMFS4 — 624 Х 365 Х г = 2,299 года; 77 х + 168 х т77г + ••• + 1260 : 1,42365 1,42 365 1,42 365 ИБ = 2,299/1,42 = 1,619 (года); Бт = 1,619 х 0,624 = 1,010256; АК= —1,010256 х 1 = —1,010256% (изменение «грязного» курса); Хнов = 62,4 — 1,010256 = 61,39% (новый «грязный» курс). 7,899 + 0,525 365 \ 0,62 0,62 ,С1 0,37 = 1,389 года; 14 х—’—п- +105 х—Чг^ + . + 651″ ’ 1,42 365 1,42 365 1,42 365 ЫБ = 1,389/1,42=0,978 года; Бт = 0,978 х 84,24/100 = 0,8238672 АК = —0,8238672 х 1 = —0,8238672% (изменение «грязного» кур­са); Кнов = 84,24 — 0,8238672 = 83,42% (новый «грязный» курс). Таким образом, дюрация ОФЗ-ФД № 27011ИМР34 больше, чем дюрация ОФЗ-ФД № 27001ИМР35. Следовательно, первая облига­ция более чувствительна к изменению процентных ставок и облада­ет повышенным уровнем процентного риска. Задача 5. Коммерческий банк решил сформировать инвестици­онный портфель из трех типов государственных облигаций: ГКО № 21139ИМР39; ОФЗ-ПД № 25021ИМР35; ОФЗ-ФД № 27001КМР35. На вторичных торгах 26 апреля 2000 г. курс этих облигаций состав­лял соответственно 98,68; 91,5 и 78,99%. Требуется рассчитать расходы банка по формированию портфе­ля (без учета комиссий и других дополнительных затрат), если структура портфеля выглядела следующим образом: ГКО — 1000 шт; ОФЗ-ПД — 2000 шт.; ОФЗ-ФД — 100 000 шт. Параметры соответствующих облигаций следует взять из преды­дущих задач. 1. Находим «чистую» стоимость каждой облигации по формуле Р1 = 1000 х 98,68/100 = 986,8 руб.; Р2 = 1000 х 91,5/100 = 915 руб.; Р3 = 10 х 78,99/100 = 7,899 руб. 2. Рассчитываем НКД (данные из предыдущих примеров): НКД ОФЗ — ПД = 40,272 руб.; НКД ОФЗ — ФД = 0,5246154 руб. Расчет цены портфеля Составим табл. 6.4 для расчета цены портфеля. Наимено­ бумаги «Чистая» стои­мость облига­ции, руб. НКД, руб. «Грязная» руб. Количество ценных бумаг, шт. Цена руб ГКО ОФЗ-ФД 986,8 0,5246154 986,8 8,4236154 1 000 2 000 100 000 986 800 1 910 544 842 361,54 Итого (2) 3 739 705,54 Таблица 6.4 Таким образом, затраты по формированию инвестиционного портфеля банка составляли 3 739 705,54 руб. Задача 6. Надо рассчитать доходность портфеля, состоящего из государственных облигаций следующих типов: ГКО № 21139ИМР39 — 1000 шт; ОФЗ-ПД № 25021ИМР35 — 2000 шт; ОФЗ-ФД № 27001ЯМР35 — 100 000 шт. На вторичных торгах 26 апреля 2000 г. курс этих облигаций со­ставил соответственно 98,68; 91,5 и 78,99%. Рассчитаем доходность к погашению по ГКО № 21139ИМР39, исходя из сложной и простой процентной ставки (данные взяты из задачи 3). Простая ставка: і = 13,95%. Сложная ставка: іе = 14,8634%. Рассчитаем доходность к погашению по ОФЗ-ПД № 25021ИМР35, исходя из сложной и простой процентной ставки (данные взяты из задачи 3). Простая ставка: і = 27,91%. Сложная ставка: іе = 30,57%. Рассчитаем доходность к погашению по ОФЗ-ФД № 27001ИМР35, исходя из сложной и простой процентной ставки (данные взяты из задачи 3): Простая ставка: I = 36,983299%. Сложная ставка: 1е = 41,67% годовых. Расчет доходности облигаций Определим доходность всего портфеля исходя из рассчитанных доходностей отдельных облигаций. Для этих целей составим табл. 6.5. Наимено­ бумаги Доход­ность по простой ставке (і), % в год Доход­ность по сложной ставке (і), % в год Количе­ство ценных бумаг в портфе­ле, шт. Р т ‘ О т Рт • От Рр Р • О і т *гт . Рт • От 1 е рр Р Р ГКО № 21139 ОФЗ-ПД ОФЗ-ФД 13,95 36,983299 14,8634 41,6700 1 000 2 000 100 000 986 800 1 910 544 842 361,54 0,263871 0,225248 3,681001 8,330418 3,922021 9,386088 Итого (Е) 3 739 705,54 1 26,2701 28,92574 Таблица 6.5 Таким образом, доходность портфеля государственных облига­ций рассчитанная на основе простой процентной ставки равна 26,27%, а на основе сложной процентной ставки — 28,93%. Состав портфеля ценных бумаг Задача 7. Требуется определить дюрацию портфеля, состоящего из различных видов государственных облигаций. Состав портфеля приводится в табл. 6.6. Наимено­ бумаги Срок до погаше­ния или дюра­ция (От), дней Количе­ство бумаг в портфе­ле (От), шт. Цена (Р руб. Став­ (іт), % О т ‘ Р т ‘ і т (О т ‘ Р т ‘ ‘ і т )/ ‘ Р т ‘ і т ) От ‘ [( О т ‘ ‘ Р т ‘ і т ) / ‘ Р т ‘ і т )] 1 2 3 4 5 6 7 8 ГКО № 21139 35 1000 986,8 0,1486 146 638,48 0,071764 2,511728 Таблица 6.6 Окончание табл. 6.6 1 2 3 4 5 6 7 8 ОФЗ-ПД № 25021 252,6 2000 955,272 0,3057 584 053,3 0,285831 72,20088 ОФЗ-ФД № 27001 509,011 150 000 8,424 0,4167 526 542,12 0,257685 131,1647 ОФЗ-ФД № 27011 830,25 100 000 6,24 0,425 265 200 0,129787 107,7554 Вексель Газпрома 82 1 940 334,64 0,315 296 205,4116 0,14496 11,88676 Вексель Сбербанка 41 1 977 014,6361 0,23 224 713,3663 0,109973 4,508888 Итого 2 043 352,679 1 330,0284 Таким образом, дюрация портфеля составляет: 2,5 + 72,2 + 131,2 + + 107,8 + 11,9 + 4,5 = 330 дней. Задача 9. Допустим, коммерческий банк должен осуществить через два года платеж на 1 000 000 руб. На рынке имеется два вида облигаций: • типа А — одногодичная дисконтная облигация номиналом 1000 руб. (ГКО); • типа В — трехгодичная купонная облигация с купонной став­кой 8% и номинальной стоимостью 1000 руб. (ОФЗ-ПД). Требуется построить портфель, полностью хеджирующий риск изменения процентной ставки при условии, что текущая процент­ная ставка равна 10%, и рассчитать, как изменится полная стои­мость портфеля для различных процентных ставок — 9, 10 и 11%. Решение. Расчет дюрации трехлетней облигации Рассчитаем дюрацию трех летней облигации (табл. 6.7). Время выплат Сумма вы­плат, руб. Ставка дисконта Приведенная те­кущая стоимость Г^РГ Первый год 80 1/1,1 = 0,9091 72,73 72,73 Второй год 80 1/1,21 = 0,8265 66,12 132,24 Третий год 1080 1/1,331 = 0,7513 811,4 2434,2 Приведенная стоимость 950,25 2639,2 Таблица 6.7 Дюрация = 2639,2/950,25 = 2,78 года. Рассчитаем число облигаций типа А и типа В в портфеле. Пусть м?1, щ — веса или пропорции по которым средства инве­стируются. Для нахождения весов надо решить систему уравнений: щ = 0,4382; щ = 0,5618. Если будущая стоимость портфеля должна быть равна 1000 000 руб., то облигаций обоих типов, с учетом текущей процентной ставки (10%), следует взять на сумму равную 1 000 000/1,21 = = 826 446,28 руб. Облигаций типа А надо купить на сумму: 826 446,28^0,4382 = = 362 149 (руб.). Облигаций типа В надо купить на сумму 826 446,28^0,5618 = = 464 297 (руб.). Структура портфеля, хеджирующего риск Представим в табл. 6.8 структуру портфеля, хеджирующего риск изменения процентных ставок (в штуках облигаций). Тип обли­гации Состав руб. Приведенная стоимость одной облигации Состав портфеля, шт. А В 362 149 464 297 1000/1,1 = 909,091 950,25 362149/909,091 = 398 464297/950,25 = 489 Таблица 6.8 Расчет портфеля облигаций для различных процентных ставок показан в табл. 6.9. Таблица 6.9 Расчет портфеля облигаций для различных процентных ставок Вид будущего дохода Доход к погашению в зависимости от процентных ставок 0,08 0,10 0,11 1 2 3 4 Сумма от реинвестиции дохода от облигации 1 на конец года 2 1000 X (1 + 0,08) X х 398 = 429 840 1000 х (1 + + 0,1) х 398 = = 437 800 1000 X 1,11 х х 398 = Окончание табл. 6.9 1 2 3 4 Сумма, полученная от 80 х (1 + 0,08) х 80 х 1,1 х 80 х 1,11 х реинвестиций купонов, х 489 = 42 249,6 х 489 = 43 032 х 489 = выданных в момент вре­ = 43 423,2 мени ґ = 1 Купоны, полученные в 80 х 489 = 39 120 80 х 489 = 80 х 489 = момент времени Т = 2 = 39 120 = 39 120 Цена продажи трехлетней 489 х 1080/(1 + 489 х 1080/ 489 х 1080/ облигации в момент вре­ + 0,08) = 489 000 /1,1 = 480 109 /1,11 = мени ґ = 2 = 475 783,78 Общая стоимость портфеля 1 000 210 1 000 061,00! 1 000 107 1 При точных расчетах данный показатель должен равняться 1 000 000 руб., но так как мы производили промежуточные округления, то произошла неболь­шая погрешность вычислений. Итак, портфель иммунизирован к риску изменения процентной ставки, но остаются риск ликвидности и риск неуплаты. В реально­сти сдвиг кривой доходности к погашению не всегда параллелен и обеспечить согласованность денежных потоков не всегда просто. Для этого нужно использовать более сложные формы кривых до­ходностей. Задача 9. Средства, инвестированные в портфель, распределены следующим образом: 35% — в актив А с доходностью 20% и стан­дартным отклонением 27,11%; 65% — в актив В с ожидаемой до­ходностью 15% и стандартным отклонением 7,75%. Коэффициент корреляции между доходностями этих активов составляет 0,5. Надо рассчитать ожидаемую доходность, а также риск портфеля и опре­делить, как изменится риск, если корреляция между активами (р) составит 1,0; 0; —0,5; —1. Решение. Ожидаемая доходность портфеля в данном случае рас­считывается по формуле Таким образом, і = (0,35 х 20) + (0,65 х 15) = 16,75%. Риск (стандартное отклонение) составит: ст = 4(0,35) 2 х (27,11) 2 + (0,65) 2 х (7,75) 2 + 2 х 0,35 х 0,65 х 27,11 х 7,75 х 0,5 = = •7163,2 = 12,8; 1) если р = 1, то ст = >/210,94 = 14,5; 2) если р = 0, то ст = ^/115,39 = 10,7; 3) если р = —0,5, то ст = -,/67,81 = 8,22; 4) если р = —1, то ст = ^/19,84 = 4,45. Задача 10. Имеется три портфеля облигаций. Необходимо про­извести оценку риска каждого портфеля (данные представлены в табл. 6.10). Таблица 6.10 Оценка риска портфеля Вид портфеля Средняя фак­тическая до­ходность, % Риск портфе­ля, % К вариац Облигации А, Б, В 23 2,8 0,122 Облигаций Г, Д, Е 26 3,3 0,127 Облигаций Ж, 3, И 25 3 0,12 Решение. Портфель облигаций Г, Д, Е — обладает наибольшим риском, так как с каждой единицей дохода связано 0,127 единицы риска. Портфель облигаций Ж, 3, И — самый низкорисковый. Задача 11. Требуется определить доходность, дюрацию, потен­циал роста и удельный потенциал роста двух вариантов портфеля, состоящего из различных долговых инструментов. Данные по каж­дому портфелю представлены в табл. 6.11. Таблица 6.11 Состав портфеля Количе­ство облигаций в порт­феле (От) Срок до погашения или дюра­ция (Лт), дней Цена руб. Ставка (Іт), % Цп *[ ( От • Р т ‘ ‘ І т)І /( Ц0т * Р т ‘ І т ) ] 1 2 3 4 5 6 Данные по портфелю А ОФ3-ПД № 25021 2000 252,6 955,272 0,3057 72,20088 ОФ3-ФД № 27011 100 000 830,25 6,24 0,425 107,7554 Окончание табл. 6.11 1 2 3 4 5 6 Данные по портфелю В ГКО № 21139 Вексель Газпрома ОФЗ-ФД № 27001 1000 150 000 35 509,011 986,8 940 334,64 8,424 0,1486 0,4167 2,511728 Решение. Рассчитаем доходность и дюрацию каждого из портфелей. Портфель А: Р = 2000*955,272 + 100 000 х 6,24 = 2 534 544 руб.; I = (0,3057 х 2000 х 955,272 + 0,425 х 100 000 х 6,24)/(2000 х х 955,272 + 100 000 х 6,24) = 0,335071 Б = 72,2 + 107,76 = 179,96 дней. Р = 1000 х 986,8 + 1 х 940 334,64 + 150 000 х 8,424 = 3 190 735 руб.; I = (0,1486 х 1000 х 986,8 + 0,315 х 1 х 940 334,64 + 0,4167 х х 150 000 х 8,424)/(1000 х 986,8 + 1 х 940334,64 + 150 000 х 8,424) = = 0,303813 Б = 2,51 + 11,89 + 131,17 = 145,57 дней. На основе рассчитаных показателей трудно выбрать «лучший» портфель, поэтому воспользуемся показателем удельного потенциа­ла роста. Сначала рассчитаем будущую стоимость каждого актива, входя­щего в портфель А и в портфель Б. Б¥25021 = 74,79 х (1 + 30,57) 365 + 1074,79 = 1160,22 руб.; БУ27011 = 0,62 х (1 + 0,425) 365 +. + 10,25 = 21,18 руб.; ^Спортф. А = 1160,22 х 2000 + 21,18 х 100 000 = 4 438 440 руб.; Портфель Б: РГ21139 = 1000 руб.; ^^газпром = 1 000 000 руб.; РУ27001 = 0,62х (1 + 0,4 1 67) 365 + . +10,37 = 15,68 руб.; БУпортф. Б = 1 000 000 + 1 000 000 + 15,68 х 150 000 = 4 352 000 (руб.) Для расчета удельного потенциала роста составим таблицу (табл. 6.12). Таблица 6.12 Расчет удельного потенциала роста Портфель Текущая цена Будущая цена рр Р^порф. _ 1 Р ^портф. т = — Б 2 534 544 3 190 735 4 438 440 4 352 000 0,751179 0,363949 0,00425 Результаты сравнения показывают, что первый вариант портфе­ля обеспечивает более эффективное вложение средств на единицу времени. Источник Читайте также:  С чего начать поиск инвестиций Оцените статью Вам также может понравиться Ящик для фермы майнинга Какие должны быть размеры у фермы для майнинга — все Ящик для майнинга шумоизоляция Подавление шума у Асиков: шумоизоляционная камера для Ящик для майнинг фермы Как собрать майнинг ферму для Ethereum в 2021 году. Ящик диких тарков окупаемость Гайд Escape from Tarkov – убежище В перерывах между Правообладателям Политика конфиденциальности