- Постановка и решение задачи оптимального распределения инвестиций
- Динамическое программирование. Задача о распределении инвестиций — видеоурок с решением задачи в Excel
- Задачи динамического программирования
- Задача распределения инвестиций
- Метод прогонки
- Задача распределения ресурсов
- Оптимальное распределение инвестиций как задача динамического программирования.
Постановка и решение задачи оптимального распределения инвестиций
Экономическая эффективность капитальных вложений (инвестиций) — одна из важнейших проблем планирования, характеризующая целесообразность вложений финансовых и других средств.
Рационального распределения инвестиций можно достигнуть лишь на основе тщательных экономических расчетов, дающих возможность определить пути достижения максимальной отдачи, т.е.
При установлении структуры инвестиций на государственном уровне необходимо исходить из предусмотренных темпов развития отраслей экономики страны, обеспеченности их основными фондами и степени использования мощностей, объема сырья и материалов, поступающих из смежных отраслей, и ряда других факторов.
Межотраслевое распределение инвестиций должно сопровождаться распределением вложений внутри отрасли и, в частности, между предприятиями, выпускающими однородную продукцию. Критерием для оптимального распределения инвестиций могут служить максимальная прибыль, максимальный суммарный прирост продукции, максимальное снижение себестоимости, максимальная занятость населения и т.п.
Задача оптимального распределения инвестиций по своей природе комбинаторная. Например, при определении фондоотдачи от 10 млрд руб. в четыре отрасли промышленности необходимо перебрать все распределения числа 10 на четыре группы. При условии распределения только из целых чисел необходимо подсчитать 286 комбинаций:
(10, 0, 0, 0); (9, 1, 0, 0); (9, 0, 1, 0); (9, 0, 0, 1) . ;
(8, 1, 1, 0); (8, 1, 0, 1); (8, 0, 1, 1); (8, 2, 0, 0); (8, 0, 2, 0); (8, 0, 0, 2);
(4, 3, 2, 1); . (4, 2, 2, 2); .
Если требуется дополнительно определить оптимальное решение задачи в случае, когда инвестиции в целом составляют 9, 8, 7, . 1 млрд руб., то необходимо провести большой объем вычислительной работы.
Метод динамического программирования позволяет находить оптимальное решение задач по распределению однородных средств между объектами при значительно меньшем, по сравнению с комбинаторным способом решения, объеме вычислительной работы.
В общем виде математическая постановка задач по распределению однородных средств (капитальных вложений, машин, сырья и т.д.) между объектами формулируется следующим образом: найти значения неизвестных xv х2, . х, . хп, т.е. план распределения, удовлетворяющий условиям:

обращающие в максимум функцию

где— сумма возможных вложений по j-му объекту (отрасль, пред
— фондоотдача по предполагаемому j-му объекту, т.е. функция 
Алгоритм, предложенный Беллманом, справедлив для функций
В задаче по распределению средств между объектами всегда предполагаются известными значения функций f.(x) при всех возможных значениях аргументов (табл. 4.7).
Источник
Динамическое программирование. Задача о распределении инвестиций — видеоурок с решением задачи в Excel
>Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и xls в архиве zip, начнется автоматически через 10 секунд. Видеоурок по решению этих задач — внизу страницы.
Указать оптимальные размеры и потоки инвестирования, если прибыль от вложений (Х i ) в проекты (А i ) распределилась следующим образом:
Теперь для решения этой задачи воспользуемся Excel .
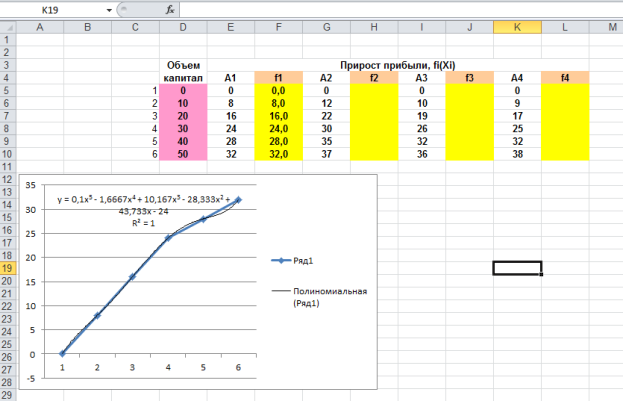
Для этого выделим шаги тренда t i , вложения x i и прибыли A i . Затем для каждого из четырех проектов построим средствами MS Excel графическую зависимость прибыли А от шага тренда ( t = 1, 2, 3, 4, 5 , 6 ). Активизируем точки графика, щелкнув по ним левой клавишей мыши, затем нажмем правую клавишу и выберем режим «Добавить линию тренда» . Для всех четырех проектов наилучшим типом является полиномиальный 5 -о й степени. С помощью полученных уравнений трендов находим теоретические значения прибыли при различных значениях шага тренда t i . Уравнения моделей тренда, коэффициенты аппроксимации и теоретические значения при были, представлены на рисунке 1.
Рис. 1. Графические зависимости прибыли от вложений и полиномиальные тренды этих зависимостей.
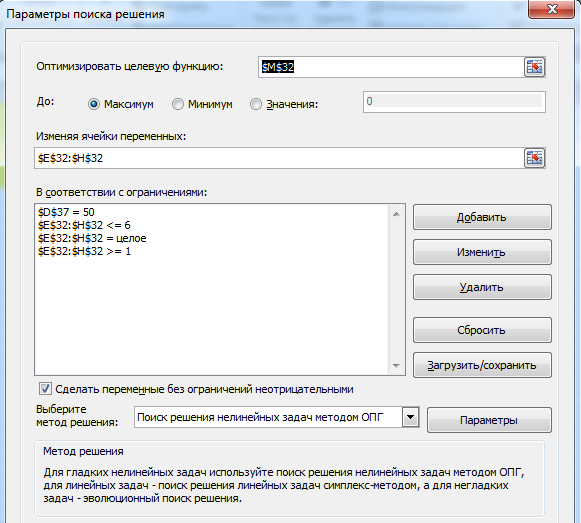
В ячейку М32 вводим выражение для общей (суммарной) прибыли, которую надо максимизировать, — это сумма всех четырех полиномиальных функций. Зависимыми переменными в этой функции являются искомые значения шагов тренда, которые будут располагаться в ячейках E 32 — H 32 . Суммарные вложения не должны превышать 5 0 тыс. ед., следовательно, вводим ограничение 1 0 *(E32+F32+G32 +H32 -4) в ячейку D 37 .
Выбираем из главного меню MS Excel режим «Поиск решения» и заполним открывшееся диалоговое окно в соответствии с требованиями. Нажмем клавишу «выполнить» и получим результат оптимизации.
Рис. 2. Модель максимизации прибыли.
Рис. 3. Оптимальное распределение капиталовложений между проектами.
Имя файла: dinprogr.zip
Размер файла: 129.98 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
Источник
Задачи динамического программирования
Данный раздел представлен следующими калькуляторами:
- Задача распределения инвестиций. Распределении инвестиций между предприятиями П1, П2. Пn. Инвестируемая сумма E усл. ден. ед.
- Задача распределения ресурсов. Планируется работа двух предприятий на n лет. Начальные ресурсы равны s0 .
- Метод прогонки.
- Задача замены оборудования.
- Складская задача: составить оптимальную программу выпуска продукции X , которая минимизирует суммарные издержки предприятия.
- Задача Джонсона.
- Задача о рюкзаке (решение задачи о загрузке транспортного средства).
- Динамическая оптимизация в планировании работ
В условиях задачи производственного планирования найти оптимальные сроки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.
Объекты / Стадии №1 №2 №3 №4 A1 2 5 4 3 A2 1 4 2 6 A3 3 4 3 4
Задача распределения инвестиций
Таблицы могут иметь разный вид.
Таблица 1 — Первый вариант таблицы исходных данных
| x | f1(x) | f2(x) | f3(x) |
| 1 | 6.3 | 4 | 5 |
| 2 | 5.2 | 6 | 7 |
| 3 | 4.3 | 4.6 | 7.8 |
| 4 | 5 | 6 | 3 |
| 5* | 7 | 6.3 | 8.2 |
* — здесь значение 5 — максимальное значение (сумма для распределения).
Таблица 2 — Второй вариант таблицы исходных данных
| x | 0 | 10 | 20 | 30 | 40 |
| f1(x) | 0 | 4 | 5 | 7 | 8 |
| f2(x) | 0 | 3 | 3 | 4 | 6 |
| f3(x) | 0 | 4 | 4 | 5 | 6 |
Пример задачи.
Для двух предприятий выделено A единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от x единиц средств, вложенных в первое предприятие, равен f1(х), а доход от y единиц средств, вложенных во второе предприятие, равен f2(y). Остаток средств к концу года составляет g1(x) для первого предприятия и g2(y) для второго предприятия. Задачу решить методом динамического программирования.
При вводе данных первую нулевую строку можно не заполнять.
В сервисе Задача распределения инвестиций используется метод обратной прогонки.
Метод прогонки
В сервисе Метод прогонки необходимо также выбрать метод решения: процедура прямой или обратной прогонки.
Источник
Задача распределения ресурсов
Пример №1 . Планируется работа двух предприятий на n лет. Начальные ресурсы равны s0. Средства x, вложенные в 1-е предприятие в начале года, дают в конце года прибыль f1(x), и возвращаются в размере g1(x). Средства y, вложенные в 2-е предприятие в начале года, дают в конце года прибыль f2(y) и возвращаются в размере g2(y). В конце года возвращенные средства заново перераспределяются между отраслями. Определить оптимальный план распределения средств и найти максимальную прибыль.
Задачу решим методом динамического программирования. Операцию управления производственным процессом разобьём на этапы. На каждом из них управление выберем так, чтобы оно приводило к выигрышу как на данном этапе, так и на всех последующих до конца операции. В этом состоит принцип оптимальности, сформулированный американским математиком А. Беллманом.
Разобьём весь период на три этапа по годам и будем нумеровать их, начиная с первого.
Обозначим через xk и yk количество средств выделяемых каждому предприятию на k-ом этапе, а через xk + yk = ak – общее количество средств на этом этапе. Тогда первое предприятие приносит на этом этапе 3 xk, а второе 4 yk единиц дохода. Общий доход на k-ом этапе 3xk + 4yk.
Обозначим через fk (ak) – максимальный доход, который получает отрасль от обоих предприятий на k-ом и всех последующих. Тогда функциональное уравнение, отражающее принцип оптимальности Беллмана, принимает вид:
fk (ak)=max<3xk + 4yk + fk+1 (ak+1)>. (1)
Так как xk + yk = ak, то yk = ak — xk и 3xk + 4yk = 3xk + 4(ak — xk) = — xk + 4ak. Поэтому fk(ak) = max<-xk + 4ak + fk+1(ak+1)>. (2)
0 ≤ xk ≤ ak
Кроме того, ak – это средства выделяемые обои предприятиям на k-ом этапе, и они определяются остатком средств, получаемых на предыдущем (k-1)-ом этапе. Поэтому по условию задачи оптимальное управление на каждом этапе
ak = 0,5xk-1 + 0,2yk-1 = 0,5xk-1+0,2(ak-1 — xk-1) = 0,3xk-1+0,2ak-1. (3)
I.Условия оптимизации
Планирование начинаем с последнего третьего этапа
Источник
Оптимальное распределение инвестиций как задача динамического программирования.
Инвестор выделяет средства в размере D условных единиц, которые должны быть распределены между n-предприятиями. Каждое k-тое предприятие при инвестировании в него средств x приносит прибыль Wk (S, xk) условных единиц, k=1. n. Нужно выбрать оптимальное распределение инвестиций между предприятиями, обеспечивающее максимальную прибыль.
Выигрышем F в данной задаче является прибыль, приносимая n-предприятиями.
Построение математической модели:
1. Определение числа шагов. Число шагов n равно числу предприятий, в которые осуществляется инвестирование.
2. Определение состояний системы. Состояние системы на каждом шаге характеризуется количеством средств Sk, имеющихся в наличии перед данным шагом, 
3. Выбор шаговых управлений. Управление на k-м шаге 
4. Функция выигрыша на k-м шаге:

это прибыль, которую приносит k-тое предприятие при инвестировании в него средств 

следовательно, данная задача может быть решена методом динамического программирования.
5. Определение функции перехода в новое состояние.

Таким образом, если на k-м шаге система находилась в состоянии 

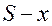



6. Составление функционального уравнения для k=n:


На последнем шаге, т.е. перед инвестированием средств в последнее предприятие, условное оптимальное управление соответствует количеству средств, имеющихся в наличии; т.е. сколько средств осталось, столько и надо вложить в последнее предприятие. Условный оптимальный выигрыш равен доходу, приносимому последним предприятием.
7. Составление основного функционального уравнения.
Подставив в формулу (53.2) выражения (53.1) и (53.3), получим следующее функциональное уравнение:

Поясним данное уравнение. Пусть перед k-м шагом у инвестора остались средства в размере 


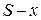




Пример: D=5000, n=3. Значения 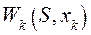

 тыс. усл. ед. тыс. усл. ед. |  тыс. усл. ед. тыс. усл. ед. |  тыс. усл.ед. тыс. усл.ед. |  тыс. усл.ед. тыс. усл.ед. |
| 1,5 | 1,7 | ||
| 2,1 | 2,4 | ||
| 2,5 | 2,3 | 2,7 | |
| 3,5 | 3,2 | ||
| 3,6 | 3,5 |
Для 

Для простоты в задаче сделано предположение, что вкладываются только тысячи условных единиц.
Проведем условную оптимизацию.
По ее результатам заполняется таблица 53.2.
| S | k=3 | k=2 | k=1 | ||
 |  |  |  |  |  |
| 1,7 | |||||
| 2,4 | 3,7 | ||||
| 2,7 | 4,4 | ||||
| 3,2 | 4,7 | ||||
| 3,5 | 1/4 | 5,2 | 6,4 |
В первой колонке таблицы записываются возможные состояния системы S=1..5, в верхней строке — номера шагов i=1..3. На каждом шаге определяются условные оптимальные управления 

· Проведение условной оптимизации для последнего шага i=3. Функциональное уравнение на последнем шаге имеет вид:

поэтому два столбца таблицы 33.2, соответствующие i=3, заполняются автоматически по таблице 33.1 исходных данных.
· Условная оптимизация для i=2. Функциональное уравнение

Для проведения условной оптимизации заполним ряд вспомогательных таблиц (таблицы 34.3—34.8), соответствующих различным значениям S, т.е. различным исходам окончания предыдущего шага.
 |  |  |  |  |
| 1,7 | 1,7 |



 |  |  |  |  |
| 2,4 | 2,4 | |||
| 1,7 | 3,7 | |||
| 2,1 | 2,1 |


 |  |  |  |  |
| 2,7 | 2,7 | |||
| 2,4 | 4,4 | |||
| 2,1 | 1,7 | 3,8 | ||
| 2,3 | 2,3 |


 |  |  |  |  |
| 3,2 | 3,2 | |||
| 2,7 | 4,7 | |||
| 2,1 | 2,4 | 4,5 | ||
| 2,3 | 1,7 | |||
| 3,5 | 3,5 |



 |  |  |  |  |
| 3,5 | 3,5 | |||
| 3,2 | 5,2 | |||
| 2,1 | 2,7 | 4,8 | ||
| 2,3 | 2,4 | 4,7 | ||
| 3,5 | 1,7 | 5,2 |
Для S=5 
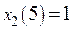

· Условная оптимизация для i=1.
Перед первым шагом состояние системы известно.
S=D=5 тыс. у.е., и условную оптимизацию следует проводить только для этого значения
S=5
 |  |  |  |  |
| 5,2 | 5,2 | |||
| 1,5 | 4,7 | 6,2 | ||
| 4,4 | 6,4 | |||
| 2,5 | 3,7 | 6,2 | ||
| 3,6 | 3,6 |



Оптимальная прибыль, приносимая тремя предприятиями при инвестировании в них 5000 у.е., равна 6,4 тыс. у.е.
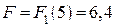
Проведем безусловную оптимизацию.
Ее результаты отмечены в таблице 34.2.
Для i=1 


Для i=2 по формуле (34.3) 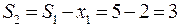


Для i=3 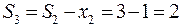



Следует пронимать, что полученное решение есть лишь некоторое приближение к оптимальному решению. Его можно улучшить, т.е. приблизить к оптимальному, взяв более мелкий шаг оптимизации, например, вкладывать в предприятия средства, кратные 500 у.е.
Теория игр. Игровые модели.
Игра – это идеализированная математическая модель коллективного поведения: несколько индивидуумов (участников, игроков) влияют на ситуацию (исход игры), причем их интересы (их выигрыши при различных возможных ситуациях) различны.
Математическая теория определяет теорию игр, как раздел математики, ориентированный на построение формальных моделей принятия оптимальных решений в ситуации конкурентного взаимодействия. Данное определение главной задачей теории игр ставит последовательность действий эффективного поведения в условиях конкуренции, конфликтности.).
В теории игр участников конкурирующего взаимодействия называют игроками, каждый из них имеет непустое множество допустимых действий, совершаемых им по ходу игры, которые называются ходами или выборами. Набор всех возможных ходов по одному из списка возможных ходов каждого игрока (участвующих в парах, тройках и т.д. ходов) называется стратегией. Грамотно построенные стратегии взаимно исключают друг друга, т.е. взаимно исчерпывают все способы поведения игроков. Исходом игры называется реализация игроком выбранной им стратегии. Каждому исходу игры соответствует определяемое игроками значение полезности (выигрыша), называемое платежом.
Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, доступности информации и т.д.
1. В зависимости от количества игроков различают парные игры и игры n игроков. Математический аппарат реализации парных игр наиболее проработан. Игры трёх и более игроков исследовать сложнее из-за трудностей технической реализации алгоритмов решения.
2. По количеству стратегий игры бывают конечные и бесконечные. Конечной называется игра с конечным числом возможных стратегий игроков. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, то игра называется бесконечной.
3. По характеру взаимодействия игры делятся на:
· бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции;
· коалиционные (кооперативные) – игроки могут вступать в коалиции.
В кооперативных играх коалиции жестко заданы на этапе постановки задачи и не могут меняться во время игры.
4. По характеру выигрышей игры делятся на:
· игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю);
· игры с ненулевой суммой.
5. По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, дуэли и др.
Матричная игра – это конечная парная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).
Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)
Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.
Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. В теории математики доказано, что игры этого класса имеют решения, однако пока не разработано практически приемлемых методов их нахождения.
Целью любой игры является максимизация каждым игроком своей выгоды. Смысл математической теории игр, построенной на приведенной выше классификации, состоит в формализации (упрощении) и облегчении оптимального выбора. Множество всех возможных стратегий игр составляет большое число, растущее тем сильнее, чем больше игроков и набор доступных каждому ходов. Так для пары игроков, если условия игры позволяют каждому совершить по n ходов, в игре существует 2 n стратегий.
Простой перебор и оценка (сравнение) такого числа стратегий представляют собой технически очень сложную задачу и неприемлемы на практике. Математический аппарат позволяет значительно снизить число требующих анализа и сравнения стратегий, отбросив заведомо неэффективные. Когда же получен ограниченный, разумный для анализа набор точек равновесия (одинаково предпочитаемых всеми игроками исходов игры), на основе анализа выигрышей игроков, выбирается наиболее рациональный результат. При выборе результата существуют два основных подхода, которые дают название окончательной стратегии игры:
· Минимаксная стратегия (выбор из максимальных (наихудших) проигрышей минимальных (наилучших).
· Максиминная стратегия (выбор из минимальных (наихудших) выигрышей максимальных (наилучших).
Развитием теории игр с использованием методов вероятностного анализа является математическая теория принятия решений. Эта теория оперирует не действительным (актуальным) решением, а средним, которое есть ожидаемое решение игры в течение ее многократного повторения. Данное свойство актуально для решения правовых задач, поскольку нормативный характер права означает, что оно ориентировано на неопределенного субъекта и предполагает многократное повторение правоотношений. Чтобы не вдаваться в глубокие математические выкладки, отметим лишь, что теория принятия решений предлагает систему критериев (например, критерий Гурвица, Хаджи-Лемана, критерий ожидаемого значения), которые с помощью вероятностного анализа исходов игр позволяют осуществить выбор оптимального решения в условиях риска и неопределенности.
Источник