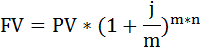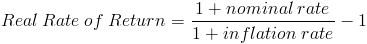Задача №33. Расчёт реального дохода вкладчика с учётом инфляции
Вклад в сумме 35000 руб. положен в банк на год с ежемесячным исчислением сложных процентов; годовая ставка по вкладам 6%; уровень инфляции за месяц 10%.
Определить:
а) сумму вклада с процентами (FV),
б) индекс инфляции за 6 месяцев (In),
в) сумму вклада с процентами с точки зрения её покупательной способности (Kr),
г) реальный доход вкладчика с точки зрения покупательной способности (d).
Решение:
а) Сумму вклада рассчитаем по формуле наращения по сложным процентам:
FV – наращенная сумма вклада,
PV – настоящая стоимость денег,
n – срок операции,
m – число раз начисления процентов в году,
j – годовая (номинальная) ставка, выраженная десятичной дробью,
j/m – процентная ставка за период
FV = 35000 * (1 + 0,06 / 12) 12*1 = 37158,72 руб.
б) Индекс инфляции за 12 месяцев найдём по формуле:
In = (1 + 0,1) 12 = 3,1384.
в) Сумму вклада с процентами с точки зрения её покупательной способности (K r ) найдём как отношение наращенной суммы вклада (FV) к индексу инфляции (In):
Kr = FV / In = 37158,72 / 3,1384 = 11839,91 руб.
г) Реальный доход вкладчика с точки зрения покупательной способности (d) вычислим так:
d = Kr – PV = 11839,91 – 35000 = – 23160,09 (реальный убыток).
Источник
Задачи по простым и сложным процентам с решением
Задача 1. Под какой процент была вложена 4000 рублей, если через 8 лет сумма наращенного капитала составила 7000 рублей.
I = S – p = 7000 – 4000 = 3000 руб .
i = 100*I/(P*n) = 100*3000/(4000*8) = 9,4%
Сумма была положена под i = 9,4%
Задача 2. Определить сумму наращенного капитала на 1 ноября, если клиент положил на депозитный счет 3 мая 15000 рублей под 15% годовых, а 2 августа ставка увеличилась на 4%. Расчеты ведутся по французской методике расчета процентов.
d 1 = с 3 мая по 2 августа = 91 день
d 2 = со 2 августа по 1 ноября = 91 день
k = 360 дней (французская методика)
I 1 = P 1* i 1* d 1/( k *100) = 15000*15*91/(100*360) = 568,75 руб.
S1= P1+I1 = 15000 + 568,75 = 15568,75 руб .
I2 = P2* i2*d2/(k*100) = 15568,75*19*91/(100*360) = 747,735 руб .
S 2 = P 2+ I 2 = 15568,75 + 747,735 = 16316,485 руб.
Сумма наращенного капитала на 1 ноября составляет 16316,485 руб.
Задачи на расчет простых и сложных %
Задача 3
1. На какой срок необходимо вложить 5000 рублей при 30% годовых, чтобы сумма дохода составила 560 рублей?
560 = (5000*30* d )/100*365;
150000* d = 20440000
Ответ: 5000 руб. надо положить на 136 дней, чтобы получить доход в 560 руб. при 30% годовых
Клиент положил в банк депозит в размере 25 000 руб. 15 апреля. 19 июня клиент снял со счета 8 000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 января по депозиту клиента составил 1000 руб. Расчеты ведутся по английской методике расчета процентов.
Р = 25000- 8000=17000 руб.
1000 = (17000* i *261)/100*365;
4437000* i = 36500000
Ответ: ставка банка по вкладу равна 8,2%
Задача 5 . На какой срок необходимо вложить 15 000 рублей при 9 % годовых, чтобы сумма дохода составила 2 000 рублей?
Для решения задачи воспользуемся формулой
i — процентная ставка;
n – срок в годах.
Из формулы получаем, что n = I *100% / P * i
n = 2 000 * 100 % / 15 000 * 9 % = 1,481 лет
Ответ: нужно вложить на 1, 481 лет.
Задача 6 . Клиент положил в банк депозит в размере 45 000 руб. 15 мая. 30 июля клиент снял со счета 7 000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 января по депозиту клиента составил 6 000 руб. Расчеты ведутся по английской методике расчета процентов.
Для решения задачи воспользуемся формулой
i — процентная ставка;
d – срок в днях, на который положили деньги;
K — база измерения времени или продолжительность года в днях.
Английская практика (в России) – 365 дней.
Из формулы получаем, что i = I * 100% * K / P * d
P = 45 000 – 7 000 = 38 000 рублей
d = (31-15) +30+31+31+30+31+30+31+1 = 231
i = 6 000 * 100 % * 365 / 38 000 * 231 = 24,95 %
Ответ: ставка банка по вкладу 24,95 %.
Под какой процент была вложена 1000 рублей, если через 7 лет сумма наращенного капитала составила 5600 рублей.
1) Процентный платеж или доход кредитора:
I = S — P = 5600 – 1000=4600 руб.
S – сумма наращенного капитала
P — первоначальный капитал
2) Процентную ставку:
i =100* I /( P * n )=100*4600/(1000*7)=66%
n — время, выраженное в годах
Ответ: процентная ставка равна 66% годовых.
Определить сумму наращенного капитала на 12 октября, если клиент положил на депозитный счет 3 апреля 20 000 рублей под 15% годовых, а 12 августа ставка увеличилась на 2%. Расчеты ведутся по немецкой методике расчета процентов.
Согласно немецкой методике год условно принимается за 360 дней, а месяц – 30 дней.
1) Количество дней, в течении которых вклад лежал под 15 % годовых:
Август – 11 дней
d = 128 дней – время пользованию ссудой
2) Количество дней, в течении вклад лежал под 17 % годовых:
Август – 19 дней
Сентябрь – 30 дней
Октябрь – 12 дней
d = 61 день – время пользованию ссудой
3) Доход, получаемый кредитором от заемщика за пользование денежной ссудой:
I = P * i * d /( k *100) = [20000*15+128/(100*360)] +[20000*17+61/(100*360)] = 1642 , 78 руб.
Р – первоначальный капитал
i – процентная ставка
d – количество дней
4) Сумма наращенного капитала:
S = P + I = 20000 + 1642,78 = 21642,78 руб.
Ответ: наращенный капитал равен 21642,78 руб.
Среднемесячная заработная плата за вычетом налогов на предприятии составила: в базисном периоде 1 1548 руб., в отчётном- 14005 руб., цены на потребительские товары и услуги повысились в отчётном периоде па 17,5%. Доля налогов в заработной плате в базисном периоде составляла 13%, в отчётном — 15%. Определите: 1 .Индекс покупательной способности денег.
2.Индекс номинальной и реальной заработной платы.
Имеются следующие данные о составе и использовании денежных доходов населения РФ в текущих ценах, млрд руб.:*
* Россия в цифрах. 2008: Стат. сб. — М.: Росстат, 2008. С. 120.
Показатель 2006 г. 2007 г .
-доходы от предпринимательской деятельности 1915,1 2118,3
-оплата труда 11237,0 14940,0
-социальные выплаты 2080,4 2317,8
-доходы от собственности 1720,6 1423,1
-другие доходы 336,8 424,3
Денежные расходы и сбережения:
-покупка товаров и оплата услуг 11927,5 14792,4
-обязательные платежи и разнообразные взносы 1813,0 2661,0
-приобретение недвижимости 572,3 690,5
-прирост финансовых активов
Определить за каждый год:
1. Номинальные и располагаемые денежные доходы населения в текущих ценах.
2. Прирост финансовых активов.
3. Структуру денежных доходов и расходов населения.
4. Изменение структуры денежных доходов населения с помощью обобщающих показателей
Больший капитал вложен на 6 месяцев при ставке 5%, а меньший на 3 месяца при ставке 6%. Разница между двумя капиталами 1000 рублей. Найти величину капиталов, если известно, что процентный платеж по первому капиталу равен двойному процентному платежу за второй капитал.
Задача на простые проценты.
Сравнить доход по различным вкладам:
1 – 5000 рублей с 1 мая по 10 ноября по 15 % годовых (английская практика расчета процентов)
2 – 4000 рублей с 5 апреля по 28 августа под 20% годовых (немецкая практика расчета процентов).
Задача на простые проценты.
По английской практике расчета процентов в году 365 дней и в месяце число дней соответствует календарю. Значит, доход по первому вкладу нужно рассчитывать на следующее количество дней: 30+30+31+31+30+31+10=193;
I 1=( P 1* i 1* d 1) / ( K 1*100)=5000*15*193/(365*100)=396,58 руб.
По немецкой практике расчета процентов в году 360 дней и 30 дней в каждом месяце. Значит, доход по первому вкладу нужно рассчитывать на следующее количество дней: 25+30+30+30+28=143
I 2=( P 2* i 2* d 2) / ( K 2 *100)=4000*20*143/(360*100)=317,78 руб.
Следовательно, доход по первому вкладу больше, чем по второму на 78,8 рублей.
Капитал величиной 15 000 рублей вложен в банк на 3 месяца под 6% годовых. Найти сумму наращенного капитала.
Решение задачи на простые проценты:
Будем решать данную задачу с использованием методики простых процентов.
Определим доход от вклада 15 000руб, положенных в банк на 3 месяца:
I = P * i * m / (12*100) = 15000*6*3/ (12*100)=225 руб.
Сумма наращенного капитала
Клиент положил в банк депозит в размере 20 000 руб. 15 мая. 10 августа клиент снял со счета 15 000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 февраля по депозиту клиента составил 11 000 руб. Расчеты ведутся по немецкой методике расчета процентов.
При определении числа дней ссуды по немецкой методике расчета процентов год условно принимается за 360 дней, а месяц – 30 дней. Учитывая это, посчитаем сколько дней составит время депозита в размере 20 000 рублей:
август – 10 дней.
Определим доход от депозитного вклада суммы 20 000 рублей на срок 85 дней:
I=(P*i*d) / (K*100)=20000*85*i/(360*100)=47,22 i.
После того, как клиент 10 августа снял со счета 15 000 рублей, сумма депозита составила 5 000 рублей. Посчитаем сколько дней составит время депозита в размере 5 000 рублей
август – 20 дней;
сентябрь – 30 дней;
октябрь – 30 дней;
ноябрь – 30 дней
декабрь – 30 дней
Тогда, I2=(P2*i*d2) / (K*100)=5000*170*i/(365*100)=23,288 i.
Определим суммарный доход от депозитного вклада:
I=I1+I2=47,22 i.+23,288 I = 70,51* i = 11000;
При заданных условиях ставка банка по вкладу составила 156%.
Под какой процент была вложена 5000 рублей, если через пять лет сумма наращенного капитала составила 3600 рублей.
По условию, была вложена сумма P =5000 рублей.
Сумма наращенного капитала I =3600 рублей.
i =3600/(5000*5)=0,144, т.е. 14,4%
Ответ: процент составляет 14,4% .
Определить сумму наращенного капитала на 1 октября, если клиент положил на депозитный счёт 3 апреля 20000 рублей под 15 % годовых, а 2 августа ставка увеличилась на 2 процента. Расчеты ведутся по немецкой методике расчета процентов.
По условию, была вложена сумма P =20000 рублей.
Размер процента составлял 15% с 3-го апреля по 2 августа и 15+2=17% -со второго августа до 1 октября.
Разобьём это время на два периода:
d 1=27+30+30+30+2=119-первый период по немецкой системе
d 2=28+30+1=59-второй период по немецкой системе
I = I 1+ I 2-наращеный капитал за два периода.
k – база дней по немецкой системе.
I=P*i*d/K=I1+I2= 20000*0,15*119/360+ 20000*0,17*59/360= 1548,99 рублей.
I 1=991,67 рублей
I 2=557,22 рублей
I =1548,99 рублей
Ответ: сумма наращенного капитала I =1548,99 рублей.
Капитал величиной 40000 рублей вложен в банк на 3 месяца под 6% годовых. Найти сумму наращенного капитала.
Клиент положил в банк депозит в размере 50000 руб. 15 мая. 10 августа клиент снял со счета 25000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 февраля по депозиту клиента составил 5000 руб. Ресчеты ведутся по немецкой методике расчета процентов.
I = I 1+ I 2; Составим уравнение, решив которое получим: i = 31.5121%
Ответ: i = 31.5121%
Под какой процент была вложена 1000 рублей, если через 7 лет сумма наращенного капитала составила 5600 рублей.
I = S — P = 5600 – 1000=4600 руб.
S — наращенный капитал
P — первоначальный капитал
Теперь определим процентную ставку:
Ответ: процентная ставка равна 15,71% годовых.
Определить сумму наращенного капитала на 12 октября, если клиент положил на депозитный счет 3 апреля 20 000 рублей под 15% годовых, а 12 августа ставка увеличилась на 2%. Расчеты ведутся по немецкой методике расчета процентов.
Немецкая методика: год условно принимается за 360 дней, а месяц – 30 дней. При определении числа дней ссуды по календарю в России первый и последний дни не учитываются.
Сосчитаем количество дней, при которых вклад лежал под 15 % годовых:
Август – 11 день
Сумма – 128 дней
И количество дней, при которых вклад лежал под 17 % годовых:
Август – 19 дней
Сентябрь – 30 дней
Октябрь – 11 день
I = P * i * d /(100*360)=[20000*15*128/36000 ]+ [20000*17*60/36000 ] = 1633,33.
I = 1633,33 рубля, где
Р – сумма вклада
i – процентная ставка
d – количество дней
S = P + I = 20000 + 1633,33 = 2163,33 рубля.
Ответ: наращенный капитал равен 2163,33 рубля.
Источник
Как правильно считать реальную доходность с учетом инфляции?
Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018
Наверно все знают, что реальная доходность — это доходность за вычетом инфляции. Все дорожает — продукты, товары, услуги. По данным Росстата за последние 15 лет цены выросли в 5 раз. Это означает, что покупательная способность денег, просто лежавших все это время в тумбочке уменьшилась в 5 раз, раньше могли купить 5 яблок, теперь 1.
Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.
Большинство инвесторов считают реальную доходность по простой формуле:
Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.
За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:
Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция
Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.
Еще одна формула, которая дает тот же результат, выглядит так:
Источник