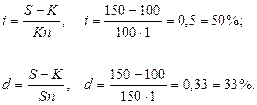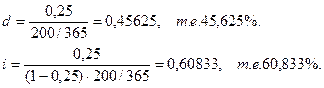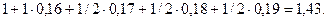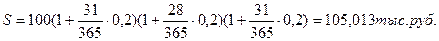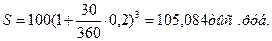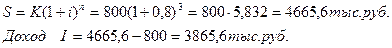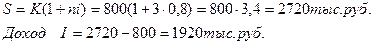Геометрическая разница, считаем реальную доходность
В прошлой публикации Где интуиция не срабатывает: считаем доходность мы рассказывали об алгебраической и геометрической суммах. Речь шла о том, как правильно считать доходность.
Когда мы употребляем термин доходность, то в большинстве случаев имеется ввиду номинальная доходность, то есть без учета инфляции. Как правило, инвестора интересует реальная доходность с учетом влияния инфляции.
Как и в прошлой статье начнем с простого примера. Если доходность депозита составила 18% годовых, а инфляция за тот же период — 11%, какова итоговая доходность?
Проверьте себя. Как бы вы посчитали результат?
Что случится, если вдруг инфляция в этот год взлетит до 118%?
Довольно часто в первом случае люди полагают, что Реальная доходность составила 7%:
Такое вычитание называется алгебраическим.
Работает ли алгебраическое вычитание во втором случае?
Может ли реальная доходность достигать -100% после учета инфляции? Это значило бы, что покупательная сила денег стала равной нулю. А если инфляция составила бы 120%, мы потеряли бы больше денег, чем у нас было? Вряд ли такой метод вычитания может быть правильным …
Как и раньше, помогает геометрическая разница:
При расчете процентные соотношения переводятся в десятичные дроби, хотя в EXCEL можно этого не делать. EXCEL умеет сам переводить из дробей в проценты и наоборот (см. прилагаемый файл).
Обобщаем
Если доходность составила R процентов, а инфляция равняется N, то реальная доходность вычисляется по формуле:
Всегда ли неправильно считать доходность через алгебраическую сумму?
В примере, когда номинальная доходность составила 18% а инфляция – 11%, можно заметить, что результаты алгебраического и геометрического вычитания довольно близки. Ошибка составит лишь 0,69%.
Действительно, иногда полезно пользоваться алгебраической разницей для получения приближенных результатов. Ошибка будет незначительной в тех случаях, когда инфляция и доходность не слишком сильно отличаются.
Тем не менее, когда рассматриваются доходности за несколько периодов или когда разница между номинальной доходностью и инфляцией значительна, величина ошибки возрастает.
Источник
Формулы доходности финансовых операций



Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что
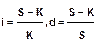
Если n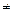
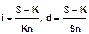
Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.
Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.
Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.
К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?
Решение:
Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.
Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.
Пусть S- размер погасительного платежа (сумма ссуды к концу срока),
dn – доля этого платежа, определяющая величину дисконта за весь срок ссуды.
К = S(1 – dn) – реально выдаваемая ссуда в момент заключения договора.
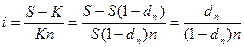 |
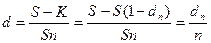 |
Задача 7.
Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.
Простые переменные ставки
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.
Если i1, i2,… ik – последовательные во времени простые ставки,
а n1, n2,… nk – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:
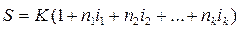 |
Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.
Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.
Множитель наращения =
Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.
Реинвестирование
В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)
В этом случае наращенная сумма для всего срока составит:
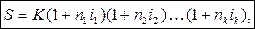
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:
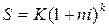
Задача 9.
Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.
По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.
По точным процентам:
(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)
По банковским процентам при условии, что в каждом месяце по 30 дней:
Модуль 2. Сложные проценты
Наращение по сложным процентам
В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.
Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.
Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) 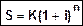
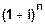
Задача 1.
Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
2. Простые проценты:
За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.
Задача 2.
Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.
Источник
Формула расчета процентов по вкладам (депозитам)
От простого к сложному.
Для начисления процентов по вкладам (депозитам), да и кредитам тоже, применяются следующие формулы:
- формула простых процентов ,
- формула сложных процентов .
Порядок начисления процентов по вышеперечисленным формулам осуществляется с использованием фиксированной или плавающей ставки. Чтобы не возвращаться к данному вопросу в дальнейшем, сразу поясню значение слов и отличия фиксированной ставки и плавающей ставки.
Фиксированная ставка, это когда установленная по вкладу банка процентная ставка, закреплена в депозитном договоре и остается неизменной весь срок вложения средств, т.е. фиксируется. Такая ставка может измениться только в момент автоматической пролонгации договора на новый срок или при досрочном расторжении договорных отношений и выплате процентов за фактический срок вложения по ставке «до востребования», что оговаривается условиями.
Плавающая ставка, это когда первоначально установленная по договору процентная ставка может меняться в течение всего срока вложения. Условия и порядок изменения ставок оговариваются в депозитном договоре. Процентные ставки могут изменяться: в связи с изменениями ставки рефинансирования, с изменением курса валюты, с переходом суммы вклада в другую категорию, и другими факторами.
Для начисления процентов с применением формул, необходимо знать параметры вложения средств на депозитный счет, а именно:
- сумму вклада (депозита),
- процентную ставку по выбранному вкладу (депозиту),
- цикличность начисления процентов (ежедневно, ежемесячно, ежеквартально и т.д.),
- срок размещения вклада (депозита),
- иногда требуется и вид используемой процентной ставки — фиксированной или плавающей.
Теперь давайте рассмотрим названные выше стандартные формулы процентов, которые применяются для расчета процентов по вкладам (депозитам).
Формула простых процентов
Формула простых процентов применяется, если начисляемые на вклад проценты причисляются к вкладу только в конце срока депозита или вообще не причисляются, а переводятся на отдельный счет, т.е. расчет простых процентов не предусматривает капитализации процентов.
При выборе вида вклада, на порядок начисления процентов стоит обращать внимание. Когда сумма вклада и срок размещения значительные, а банком применяется формула простых процентов, это приводит к занижению суммы процентного дохода вкладчика. Формула простых процентов по вкладам выглядит так:
Значение символов:
S — сумма денежных средств, причитающихся к возврату вкладчику по окончании срока депозита. Она состоит из первоначальной суммы размещенных денежных средств, плюс начисленные проценты.
I – годовая процентная ставка
t – количество дней начисления процентов по привлеченному вкладу
K – количество дней в календарном году (365 или 366)
P – первоначальная сумма привлеченных в депозит денежных средств
Sp – сумма процентов (доходов).
А чтобы рассчитать только сумму простых процентов формула будет выглядеть так:
Значение символов:
Sp – сумма процентов (доходов).
I – годовая процентная ставка
t – количество дней начисления процентов по привлеченному вкладу
K – количество дней в календарном году (365 или 366)
P – сумма привлеченных в депозит денежных средств.
Приведу условные примеры расчета простых процентов и суммы банковского депозита с простыми процентами:
Пример 1. Предположим, что банком принят депозит в сумме 50000 рублей на срок 30 дней. Фиксированная процентная ставка — 10,5 % «годовых». Применяя формулы, получаем следующие результаты:
S = 50000 + 50000 * 10,5 * 30 / 365 / 100 = 50431,51
Sp = 50000 * 10,5 * 30 / 365 / 100 = 431,51
Пример 2. Банком принят депозит в той же сумме 50000 рублей сроком на 3 месяца (90 дней) по фиксированной ставке 10,5 процентов «годовых». В условиях поменялся только срок вложения.
S = 50000 + 50000 * 10,5 * 90 / 365 / 100 = 51294,52
Sp = 50000 * 10,5 * 90 / 365 / 100 = 1294,52
При сравнении двух примеров видно, что сумма ежемесячно начисленных процентов по формуле простых процентов не меняется.
431,51 * 3 месяца = 1294,52 рубля.
Пример 3. Банком принят депозит в сумме 50000 рублей сроком на 3 месяца (90 дней) по фиксированной ставке 10,5 процентов «годовых». Вклад пополняемый, и на 61 день произведено пополнение вклада в сумме 10000 рублей.
S1 =50000 + 50000 * 10,5 * 60 / 365 / 100 = 50863.01
Sp1 = 50000 * 10,5 * 60 / 365 / 100 = 863.01
S2 = 60000 + 60000 * 10,5 * 30 / 365 / 100 = 60517.81
Sp2 = 60000 * 10,5 * 30 / 365 / 100 = 517.81
Sp = Sp1 + Sp2 = 50000 * 10,5 * 60 / 365 / 100 + 60000 * 10,5 * 30 / 365 / 100 = 863,01 + 517,81 = 1380,82
Пример 4. Банком принят депозит в той же сумме 50000 рублей сроком на 3 месяца (90 дней), по плавающей ставке. На первый месяц (30 дней) процентная ставка — 10,5 %, на последующие 2 месяца (60 дней) процентная ставка – 12 %.
S1 = 50000 + 50000 * 10,5 * 30 / 365 / 100 = 50000 + 431,51 = 50431.51
Sp1 = 50000 * 10,5 * 30 / 365 / 100 = 431,51
S2 = 50000 + 50000 * 12 * 60 / 365 / 100 = 50000 + 986,3 = 50986.3
Sp2 = 50000 * 12 * 60 / 365 / 100 = 986,3
Sp = 50000 * 10,5 * 30 / 365 / 100 + 50000 * 12 * 60 / 365 / 100 = 431,51 + 986,3 = 1417,81
Формула сложных процентов
Формула сложных процентов применяется, если начисление процентов по вкладу, осуществляется через равные промежутки времени (ежедневно, ежемесячно, ежеквартально) а начисленные проценты причисляются к вкладу, т. е. расчет сложных процентов предусматривает капитализацию процентов (начисление процентов на проценты).
Большинство банков, предлагают вклады с поквартальной капитализацией (Сбербанк России, ВТБ и т. д.), т.е. с начислением сложных процентов. А некоторые банки, в условиях по вкладам предлагают капитализацию по окончанию срока вложения, т.е. когда вклад пролонгируется на следующий срок, что, мягко говоря, относится к рекламному трюку, который подталкивает вкладчика не забирать начисляемые проценты, но само начисление процентов фактически осуществляется по формуле простых процентов. И повторюсь, когда сумма вклада и срок размещения значительные, такая «капитализация» не приводит к увеличению суммы процентного дохода вкладчика, ведь начисления процентов на полученные в предыдущих периодах процентные доходы нет.
Формула сложных процентов выглядит так:
Значение символов:
I – годовая процентная ставка;
j – количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов;
K – количество дней в календарном году (365 или 366);
P – первоначальная сумма привлеченных в депозит денежных средств;
n — количество операций по капитализации начисленных процентов в течение общего срока привлечения денежных средств;
S — сумма денежных средств, причитающихся к возврату вкладчику по окончании срока депозита. Она состоит из суммы вклада (депозита) с процентами.
Расчет только сложных процентов с помощью формулы, будет выглядеть так:
Значение символов:
I – годовая процентная ставка;
j – количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов;
K – количество дней в календарном году (365 или 366);
P – первоначальная сумма привлеченных в депозит денежных средств;
n — количество операций по капитализации начисленных процентов в течение общего срока привлечения денежных средств;
Sp – сумма процентов (доходов).
Приведу условный пример расчета сложных процентов и суммы банковского депозита со сложными процентами:
Пример 5. Принят депозит в сумме 50 тыс. руб. сроком на 90 дней по фиксированной ставке 10,5 процентов годовых. Начисление процентов – ежемесячно. Следовательно, количество операций по капитализации начисленных процентов (п) в течение 90 дней составит – 3. А количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов (j) составит – 30 дней (90/3). Какова будет сумма процентов?
S = 50000 * (1 + 10,5 * 30 / 365 / 100)3 = 51305,72
Sp = 50000 * (1 + 10,5 * 30 / 365 / 100)3 — 50000 = 1305,72
Убедиться в правильности суммы процентов, рассчитанный по методу сложных процентов можно, перепроверив расчет с помощью формулы простых процентов.
Для этого разобьем срок депозита на 3 самостоятельных периода(3 месяца) по 30 дней и рассчитаем проценты для каждого периода, использую формулу простых процентов. Сумму депозита в каждом следующем периоде будем брать с учетом процентов за предыдущие периоды. В результате расчета получилось:
| месяцы | Р – сумма депозита | I -Процентная ставка | t – количество дней начисления процентов | Sp – сумма процентов | S -суммы размещенных денежных средств + начисленные проценты. (2+5) |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 50000.00 | 10.5 | 30 | 431.51 | 50431.51 |
| 2 | 50431.51 | 10.5 | 30 | 435.23 | 50866.74 |
| 3 | 50866.74 | 10.5 | 30 | 438.98 | 51305.72 |
Итак, общая сумма процентов с учетом ежемесячной капитализации (начисления процентов на проценты) составляет:
Sp = Sp1 + Sp2 + Sp3 = 431,51 + 435,23+ 438,98 = 1305,72
Это соответствует сумме, рассчитанной по сложным процентам в примере № 5.
А при расчете процентов за этот же период по формуле простых процентов в примере №2, доход составил только 1294,52 руб. Капитализация процентов принесла вкладчику дополнительно 11,2 руб. (1305,72 – 1294,52), т.е. большая доходность получается у вкладов с капитализацией процентов, когда применяются сложные проценты.
При начислении процентов необходимо учитывать и еще один маленький нюанс. При определении количества дней начисления процентов по вкладу (t) или количества календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов (j), не учитывается день закрытия (снятия) вклада. Так, например, 02.11.07 банк принял депозит сроком на 7 дней. Полный срок депозита с 02.11.07 по 09.11.07, т.е. 8 календарных дней. А период начисления процентов по депозиту будет с 02.11.07 по 08.11.07, т.е. – 7 календарных дней. День 09.11.07 в расчет не принимается т.к. депозит возвращен клиенту.
Заканчивая материал, хочу еще раз обратить ваше внимание на то, что по приведенным формулам процентов можно производить и расчеты процентов по кредитам. Удачного вам подсчета своих доходов и расходов.
Источник