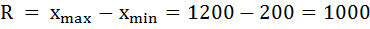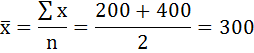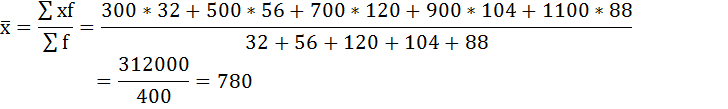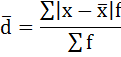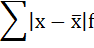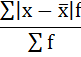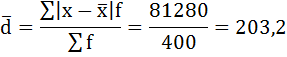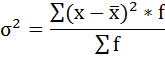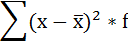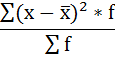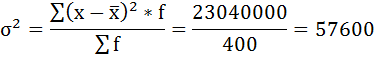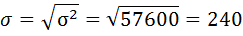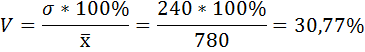Коэффициент вариации (CV)
Коэффициент вариации (coefficient of variation, CV) – это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.
Понимание коэффициента вариации
Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.
Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.
Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.
Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.
Обычно данный коэффициент используют в таких целях как:
- Для сравнения нескольких различных рядов данных или показателей;
- Для оценки потенциальных объектов инвестирования;
- Для проведения XYZ-анализа.
КЛЮЧЕВЫЕ МОМЕНТЫ
- CV – это статистическая мера дисперсии в ряду данных вокруг среднего значения;
- В финансах CV позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций;
- Чем ниже величина отношения стандартного отклонения к средней доходности,тем лучше соотношение риска и доходности.
Формула CV
Ниже приведена формула для расчета коэффициента вариации:
Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.
Коэффициент вариации в Excel и Open Office
Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.
В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.
Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:
Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:
Аналогичным образом рассчитаем среднее значение для каждого ряда данных:
Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:
Кликните по картинке для увеличения
Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.
Пример использования коэффициента вариации для выбора объекта инвестиций
Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.
Для принятия решения инвестором используется следующая 15-летняя историческая информация:
- SPDR S&P 500 ETF имеет среднюю годовую доходность 5,47% и стандартное отклонение 14,68%. Коэффициент вариации SPDR S&P 500 ETF составляет 2,68;
- Средняя годовая доходность Invesco QQQ ETF составляет 6,88%, а стандартное отклонение-21,31%. Коэффициент вариации QQQ равен 3,09;
- iShares Russell 2000 ETF имеет среднюю годовую доходность 7,16% и стандартное отклонение 19,46%. Коэффициент вариации IWM равен 2,72.
Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.
Источник
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | 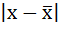 | 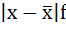 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | 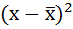 | 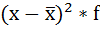 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Источник