Распределения вероятностей и ожидаемая доходность
Поскольку риск связан с вероятностью того, что фактическая доходность будет ниже ее ожидаемого значения, распределения вероятностей являются основой для измерения риска. Предположим, например, что вы финансовый менеджер фирмы, которая решила инвестировать 100 000 долларов сроком на один год. В таблице 1 приведены четыре альтернативных варианта инвестиций:
1. Казначейские векселя (Т-векселя) со сроком погашения один год и ставкой дохода 8%, которые могут быть приобретены с дисконтом (т.е. по цене ниже номинала); в момент погашения будет выплачена их номинальная стоимость.
2. Корпорационные облигации, которые продаются по номиналу с купонной ставкой 9% (т.е. на 100 000 долларов вложенного капитала можно получать 9000 долларов годовых) и сроком погашения 10 лет. Однако ваша фирма планирует продать эти облигации в конце первого года. Следовательно, фактическая доходность по облигациям будет зависеть от уровня процентных ставок на конец года. Этот уровень в свою очередь зависит от состояния экономики на конец года: быстрые темпы экономического развития, вероятно, вызовут повышение процентных ставок, что снизит рыночную стоимость облигаций, в случае экономического спада возможна противоположная ситуация.
3. Проект капиталовложений №1, чистая стоимость которого составляет 100 000 долларов. Денежный поток в течение года равен нулю, все выплаты осуществляются в конце года. Сумма этих выплат зависит от состояния экономики.
4. Альтернативный проект капиталовложений №2, совпадающий по всем параметрам с проектом №1 и отличающийся от него лишь распределением вероятностей ожидаемых в конце года выплат.
Распределением вероятностей называется множество возможных исходов с указанием вероятности появления каждого из них. Таким образом, в таблице 1 представлены четыре распределения вероятностей, соответствующие четырем альтернативным вариантам инвестирования. Доходность по казначейским векселям точно известна — она составляет 8% и не зависит от состояния экономики. Таким образом, риск по казначейским векселям равен нулю.
Отметим, что инвестиции в казначейские векселя являются безрисковыми только в том смысле, что их номинальная доходность не изменяется в течение данного периода времени. Реальная же доходность казначейских векселей содержит определенную долю риска, поскольку она зависит от фактических темпов роста инфляции в течение периода владения векселями. Более того, казначейские векселя могут представлять проблему для инвестора, который обладает портфелем ценных бумаг с целью получения непрерывного дохода: когда истекает срок платежа по казначейским векселям, необходимо осуществить реинвестирование денежных средств и если процентные ставки снижаются, доход портфеля также уменьшится.
Этот вид риска, который носит название риска нормы реинвестирования, не учитывается в нашем примере, так как период, в течение которого фирма владеет векселями, соответствует сроку их погашения. Наконец, отметим, что релевантная доходность любых инвестиций — это доходность после уплаты налогов, поэтому, значения доходности, используемые для принятия решения, должны отражать доход за вычетом налогов.
По трем другим вариантам инвестирования реальные, или фактические, значения доходности не будут известны до окончания соответствующих периодов владения активами. Поскольку значения доходности не известны с полной определенностью, эти три вида инвестиций являются рисковыми.
Оценка доходности по четырем инвестиционным альтернативам
| Таблица 1 | |||||
| Доходность инвестиций при данном состояния экономики, % | |||||
| Состояние экономики | Вероятность | Казначейские векселя, % | корпорационные облигации | проект №1 | проект №2 |
| Глубокий спад | 0,05 | 80 | 12,0 | — 3,0 | — 2,0 |
| Незначительный спад | 0,20 | 80 | 10,0 | 6,0 | 9,0 |
| Стагнация | 0,5 | 80 | 9,0 | 11,0 | 12,0 |
| Незначительный подъем | 0,20 | 80 | 8,5 | 14,0 | 15,0 |
| Сильный подъем | 0,05 | 80 | 8,0 | 19,3 | 26,0 |
| ____________________________________________________________________________________ | |||||
| Ожидаемая доходность | — | 80 | 9,2 | 10,3 | 12,0 |
Примечание. Доходность, соответствующую различным состояниям экономики следует рассматривать как интервал значений, а отдельные ее значения — как точки внутри этого интервала. Например, 10%-ная доходность облигации корпорации при незначительном спаде представляет собой наиболее вероятное значение доходности при данном состоянии экономики, а точечное значение используется для удобства расчетов.
Распределения вероятностей бывают дискретными или непрерывными. Дискретное распределение вероятностей имеет конечное число исходов; так, в таблице 1 приведены дискретные распределения вероятностей. Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов. Каждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облигаций составит 9%, равна 0.50.
Если умножить каждый исход на вероятность его появления, а затем сложить полученные результаты, мы получим средневзвешенную исходов. Весами служат соответствующие вероятности, а средневзвешенная представляет собой ожидаемое значение. Так как исходами являются доходности, ожидаемое значение — это ожидаемая доходность (expected rate of return, k), которую можно представить в следующем виде:
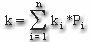
ki — i-й возможный исход,
Рi — вероятность появления i-го исхода,
n — число возможных исходов.
Используя формулу, находим, что ожидаемая доходность проекта 2 равна 12.0%
к = -2.0% * 0.05 + 9.0% * 0.20 + 12.0% * 0.50 + 15%* 0.20 + 26.0% * 0.05 = 12.0%
Ожидаемые доходности трех других альтернативных вариантов инвестирования найдены аналогичным образом (таблице 1).
Дискретные распределения вероятностей могут быть представлены графически или в табличной форме. На рисунке 1 приведены столбиковые диаграммы (или гистограммы) проектов №1 и №2.
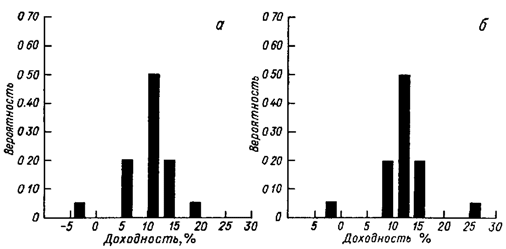
Рисунок 1. Графическое представление дискретного распределения вероятностей; а — проект №1; б — проект №2
Возможные значения доходности проекта №1 принадлежат промежутку от -3.0 до +19.0%, а проекта №2 от -2.0 до +26.0%. Отметим, что высота каждого столбца представляет собой вероятность появления соответствующего исхода, а сумма этих вероятностей по каждому варианту равна 1.00. Отметим также, что распределение значений доходности проекта №2 симметрично, тогда как соответствующее распределение для проекта №1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначейских векселей представлена единственным столбцом, а доходность корпорационных облигаций представлена диаграммой, имеющей правостороннюю асимметрию.
Программная реализация данной методики финансовой математики сделана в: «Альтаир Финансовый калькулятор 2.xx».
На примере расчета ожидаемой доходности можно увидеть, как применять программу «Альтаир Финансовый калькулятор 2.xx» на практике.

Главная 



Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.
Источник
CFA — Нормальное распределение вероятностей
Нормальное распределение — это наиболее часто используемое распределение вероятностей в количественной финансовой практике. Оно играет ключевую роль в современной портфельной теории и ряде технологий управления рисками. Рассмотрим эту концепцию в рамках изучения количественных методов по программе CFA.
Поскольку нормальное распределение вероятностей имеет так много применений, профессионалы в области финансов и инвестиций должны тщательно его изучить.
Роль нормального распределения в статистических выводах и регрессионном анализе значительно расширена благодаря центральной предельной теореме. Центральная предельная теорема (англ. ‘central limit theorem’) утверждает, что сумма (и среднее) большого числа независимых случайных величин приблизительно нормально распределена.
Французский математик Абрахам Де Муавр (Abraham de Moivre, 1667-1754) ввел понятие нормального распределения в 1733 году при разработке своей версии центральной предельной теоремы.
Как показано на Рисунке 5, нормальное распределение является симметричным и имеет колоколообразную форму.
Диапазоном возможных исходов нормального распределения является вся вещественная ось: все действительные числа, лежащих между \(-\infty\) и \(+\infty\). Хвосты колоколообразной кривой распространяются без ограничений слева и справа.
Определяющими характеристиками нормального распределения являются:
Нормальное распределение полностью описывается двумя параметрами — ее средним значением, \( \mu \), и дисперсией, \( \sigma^2 \). Обозначим это как \( X \sim N (\mu, \sigma^2) \) (читается «X имеет нормальное распределение со средним \(p\) и дисперсией \(\sigma^2\)» ).
Мы также можем определить нормальное распределение с точки зрения среднего и стандартного отклонения, \( \sigma \) (часто это удобно, так как \( \sigma \) измеряется в тех же единицах, что и \(X\) и \(\mu\)). Как следствие, мы можем ответить на любой вопрос о вероятности нормальной случайной величины, если мы знаем его среднее значение и дисперсию (или стандартное отклонение).
Нормальное распределение имеет асимметрию 0 (симметрично). Нормальное распределение имеет эксцесс (мера крутизны или островершинности распределения) 3; его избыточный эксцесс (эксцесс — 3.0) равен 0.
Если мы имеем выборку размера \(n\) из нормального распределения, мы хотим знать о возможном изменении в асимметрии и эксцессе выборки. Для нормальной случайной величины, стандартное отклонение ассиметрии выборки равно \(6/n\), стандартное отклонение эксцесса выборки равно \( 24/n \).
Как следствие симметрии, среднее, медиана и мода равны для нормальной случайной величины.
Линейная комбинация двух или более нормальных случайных величин также распределена нормально.
Перечисленное выше касается только одной переменной величины или одномерного нормального распределения: распределения одной нормальной случайной величины. Одномерное распределение (англ. ‘univariate distribution’) описывает одну случайную величину.
Многомерное распределение (англ. ‘multivariate distribution’) определяет вероятности для группы связанных случайных величин. Вы столкнетесь с многомерным нормальным распределением (англ. ‘multivariate normal distribution’) в инвестиционной деятельности и должны знать о нем следующее.
Когда мы имеем группу финансовых активов, мы можем моделировать распределение доходности для каждого актива в отдельности, или распределение доходности для активов как для группы. «Как для группы» означает, что мы принимаем во внимание всех статистических взаимосвязей между доходностью активов.
Одна из моделей, которая часто используется для оценки доходности ценных бумаг, является многомерным нормальным распределением. Многомерное нормальное распределение для доходности ценных бумаг полностью определяется этими тремя списками параметров:
- списком средних ставок доходности по отдельным ценным бумагам (всего \(n\) средних всего);
- списком дисперсий доходности ценных бумаг (всего \(n\) дисперсий); а также
- списком всех отчетливых попарных корреляций доходности (всего \(n (n — 1) / 2\) различных корреляций).
Например, распределение для двух акций (двумерное нормальное распределение) имеет 2 средние, 2 дисперсии и 1 корреляцию: \( 2 (2 — 1) / 2\).
Распределение для 30 акций имеет 30 средних, 30 дисперсий и 435 различных корреляций: \(30(30 — 1)/2 \).
Корреляция доходности акций Dow Chemical с акциями American Express такая же, как корреляция American Express с Dow Chemical, поэтому они считаются одной отчетливой корреляцией.
Необходимость в указании корреляций является отличительной чертой многомерного нормального распределения в отличии от одномерного нормального распределения.
Формулировка «предположим, что ставки доходности нормально распределены» или «предположим, что ставки доходности соответствуют нормальному распределению» иногда используется для обозначения совместного нормального распределения для нескольких ценных бумаг.
Для портфеля из 30 ценных бумаг, например, доходность портфеля представляет собой средневзвешенное значение доходности 30 ценных бумаг. Средневзвешенное значение представляет собой линейную комбинацию. Таким образом, портфель доходности нормально распределен, если доходность отдельных ценных бумаг (совместно) нормально распределена.
Напомним, что для того, чтобы указать нормальное распределение доходности портфеля, нам нужны средние значения, дисперсии, и отчетливые парные корреляции ценных бумаг портфеля.
Имея все это в виду, мы можем вернуться к нормальному распределению для одной случайной величины. Кривые на графике Рисунка 5, являются функцией плотности нормального распределения:
Доходность опционов ассиметрична. Поскольку нормальное распределение является симметричным распределением, мы должны быть осторожными в его использовании для моделирования доходности портфелей, содержащих значительные позиции по опционам.
Нормальное распределение, однако, менее подходит в качестве модели для цен на активы, чем в качестве модели для доходности активов. Нормальная случайная величина не имеет нижнего предела. Эта характеристика имеет несколько последствий для применения нормальных распределений в инвестициях. Цена актива может упасть только до 0 и в этот момент финансовый актив становится бесполезным.
В результате, на практике, финансовые аналитики, как правило, не используют нормальное распределение для моделирования распределения цен на активы. Также обратите внимание, что переход от цены актива любого уровня до 0 означает доходность -100%. Поскольку нормальное распределение распространяется ниже 0 без ограничений, оно не может быть полностью точной моделью для доходности активов.
Установив, что нормальное распределение является подходящей моделью для интересующей нас случайной величины, мы можем использовать его, чтобы сделать следующие вероятностные утверждения:
- Приблизительно 50% всех наблюдений попадают в интервал \( \mu \pm (2/3) \sigma \).
- Приблизительно 68% всех наблюдений попадают в интервал \( \mu \pm \sigma \).
- Приблизительно 95% всех наблюдений попадают в интервал \( \mu \pm 2 \sigma \).
- Приблизительно 99% всех наблюдений попадают в интервал \( \mu \pm 3 \sigma \).
Интервалы в один, два и три стандартных отклонения показаны на Рисунке 6. Эти доверительные интервалы легко запомнить, но они лишь приблизительные для указанных вероятностей. Более точные интервалы составляют \( \mu \pm 1.96\sigma \) для 95% наблюдений и \( \mu \pm 2.58\sigma \) для 99% наблюдений.
В целом, мы не наблюдаем среднее или стандартное отклонение генеральной совокупности распределения, поэтому нам нужно оценить их.
Генеральная совокупность — это все элементы указанной группы, и математическое ожидание представляет собой среднее арифметическое, рассчитанное для совокупности.
Выборка представляет собой подмножество генеральной совокупности, и выборочное среднее представляет собой среднее арифметическое для выборки.
Для получения более подробной информации об этих понятиях см. чтение о статистических концепциях и рыночной доходности.
Мы вычисляем среднее совокупности, \(\mu\), используя выборочное среднее, \( \overline X \) (иногда обозначаемое как \( \hat <\mu>\) ) и вычисляем стандартное отклонение, \(\sigma \), используя стандартное отклонение выборки, \( s \) (иногда обозначаемое как \( \hat <\sigma>\) ).
Существует столь же много различных нормальных распределений, сколько средних (\(\mu\)) и дисперсий ( \(\sigma^2 \)). Мы можем ответить на все поставленные выше вопросы с точки зрения любого нормального распределения. Электронные таблицы, например, имеют функции для расчета нормальной кумулятивной функции распределения с любыми спецификациями среднего и дисперсии.
Ради эффективности, однако, мы хотели бы свести все вероятностные утверждения к одному нормальному распределению. Стандартное нормальное распределение (нормальное распределение с \( \mu = 0 \) и \( \sigma = 1 \) ) как раз и выполняет эту роль.
Есть два шага в стандартизации случайной величины \( X \): вычесть среднее \( X \) из \( X \), а затем разделить результат на стандартное отклонение \( X \). Если у нас есть список наблюдений для нормальной случайной величины \( X \), мы вычитаем среднее из каждого наблюдения, чтобы получить список отклонений от среднего значения, а затем разделить каждое отклонение на стандартное отклонение.
Результатом является стандартная нормальная случайная величина, \( Z \) (символ \(Z \) используется по соглашению в качестве символа для стандартной нормальной случайной величины).
Если мы имеем выражение \( X \sim N(\mu, \sigma^2) \) (читается «X следует нормальному распределению с параметрами \( \mu \) и \( \sigma^2 \)» ), мы стандартизируем его, используя формулу:
Предположим, что мы имеем нормальную случайную величину, \( X \), при \( \mu = 5 \) и \( \sigma = 1.5 \). Мы стандартизируем X с помощью выражения: \( Z = (Х — 5) /1.5 \). Например, значение \( Х = 9.5 \) соответствует стандартизованному значению 3, рассчитанному как \( Z = (9.5 — 5)/1.5 = 3 \).
Вероятность того, что мы будем наблюдать значение, не превышающее 9.5 для \( X \sim N(5,1.5) \) точно такая же, как вероятность того, что мы будем наблюдать значение, не превышающее 3 для \( Z \sim N(0.1) \).
Мы можем ответить на все вопросы о вероятности \( X \), используя стандартные значения и вероятностные таблицы для Z. Как правило, мы не знаем среднее и стандартное отклонения генеральной совокупности, поэтому мы часто используем выборочное среднее \( \overline X \) для \( \mu \) и стандартное отклонение выборки \( s \) для \( \sigma \).
Стандартные нормальные вероятности также можно вычислить с помощью электронных таблиц, статистического и эконометрического программного обеспечения и языков программирования.
В Таблице 5 приведены выдержки из таблиц кумулятивной функции распределения для стандартной нормальной случайной величины. По соглашению \( N(x) \) обозначает кумулятивную функцию распределения (cdf) для стандартной нормальной случайной величины.
Другим часто использующимся обозначением cdf стандартной нормальной случайной величины является \( \Phi (х) \).
Источник