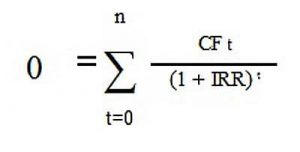Расчет внутренней нормы доходности при постоянной барьерной ставке

Расчет внутренней нормы доходности

Ни один инвестор не вкладывает средства слепо, не проведя предварительных исследований: он должен быть уверен, что они окупятся или, как минимум, их удастся вернуть. Для этого оценивается потенциальная рентабельность инвестиционного проекта. Конечно, это нельзя сделать иначе как комплексно, применяя ряд специально разработанных показателей, важнейший из которых – внутренняя норма доходности.

Рассмотрим, в чем особенности метода инвестиционных исследований, основанного на вычислении внутренней нормы доходности – IRR.

Что такое внутренняя норма доходности?

Никто не может рассчитать с вероятностью 100%, какой доход удастся получить от вложенных средств. Слишком много переменных факторов, могущих повлиять на реализацию бизнес-проекта, профинансированного инвестором. Однако можно максимально снизить риск неточностей, если применить не абсолютную, а относительную оценку.

Та процентная ставка, при которой инвестор гарантированно возместит свое вложение, но не получит прибыли, называется внутренней нормой доходности (ВНД). Норма заключается в том, что все денежные потоки данного инвестиционного проекта в сумме взаимозачтутся. Иначе говоря, расходы на инвестиционный проект в какой-то момент времени уравновешиваются полученными доходами (говорят, что проект «вышел в ноль»).

ВАЖНО! Слово «внутренняя» в определении данной нормы инвестиционных вложений означает ее зависимость от свойств самого проекта, а не от внешних факторов.

Внутреннюю норму доходности специалисты могут именовать по-разному. Встречаются следующие наименования:

• ВНД – русская аббревиатура;
• IRR – английская аббревиатура от «Internal Rate of Return» – «внутренняя норма доходности»;
• внутренняя норма рентабельности;
• внутренняя норма прибыли;
• внутренняя норма возврата инвестиций;
• предельная эффективность капитальных вложений;
• процентная норма прибыли;
• дисконтированный поток реальных денег;
• финансовая норма прибыли;
• собственная норма прибыли.

ВНИМАНИЕ! Эту норму можно счесть предельной, поскольку выход за ее пределы уже означает для инвестора убыток.

Показатели для расчета IRR

Математически расчет внутренней нормы доходности не так уж сложен, но формула включает много дополнительных показателей, которые необходимо учитывать. Среди них:

• NPV – от первых букв выражения «Net Present Value» («чистая приведенная стоимость») – сумма всех денежных потоков данного проекта, приведенная к общему показателю при взаимозачете доходов и затрат;
• CF – денежные потоки (от «Cash Flows») – величины различных притоков и оттоков финансов, в том числе и инвестируемых средств, в выбранный период времени t (обычно берется год). Для инвестиционного проекта первый денежный поток – сама инвестиция – естественно, будет иметь отрицательное значение (это затрата).
• R – ставка дисконтирования, то есть тот процент, под который инвестор может получить средства для вложений (взять банковский кредит, продать свои акции или использовать внутренние средства).
• WACC – средневзвешенная стоимость капитала (от Weighted Average Cost of Capital) – если применяется сразу несколько источников привлечения денег, то процентная ставка будет представлять среднюю величину, рассчитанную пропорционально.

ВАЖНАЯ ИНФОРМАЦИЯ! Было бы очень просто рассчитать внутреннюю норму доходности, зная все необходимые показатели. Однако на практике невозможно определить точные величины денежных потоков и однозначно вычислить ставку дисконтирования. Поэтому для каждого отдельного проекта оценивают степень зависимости NPV от процентной ставки.

Формула расчета внутренней нормы рентабельности

IRR – это такая величина R, при которой NPV равен нулю. Поэтому этот показатель можно вывести из формулы расчета приведенной суммы денежных потоков.

• 0 означает величину NPV;
• n – количество исследуемых временных периодов;
• CF_t – денежные потоки в учетный момент времени.

Способы вычисления ВНД

Посчитать значение внутренней нормы доходности вручную не представляется возможным, так как, если вывести из него значение IRR, оно получится множителем 4 степени. Вычислить этот показатель можно несколькими способами:

• использовать специальный финансовый калькулятор;
• применить программу Excel, в которой эта функция встроена в раздел «Финансовые формулы» под названием ВСД («внутренняя ставка доходности»);
• воспользоваться одним из онлайн-калькуляторов;
• применить графический способ (использовался до широкого распространения Персональных компьютеров).

Достоинства и недостатки метода IRR

Для оценки инвестиционных возможностей главным образом применяются два метода – вычисление NPV и IRR. Метод определения внутренней нормы доходности относителен, поэтому не может претендовать на высокую точность, однако обладает рядом преимуществ:

• помогает достаточно просто оценить рентабельность инвестиционного проекта;
• показывает максимально допустимый размер затрат для вложения в проект;
• позволяет сравнивать различные проекты по рентабельности, даже если они отличаются по масштабу и протяженности во времени.

Недостатки метода IRR:

• нельзя посчитать абсолютную доходность инвестиции (то есть сколько конкретно денег – рублей, валюты – она может принести инвестору);
• возможно завышение инвестиционного эффекта, если ВНД сильно отличается от уровня реинвестиций компании (то есть положительные денежные потоки «возвращаются» инвестору с процентной ставкой, не совпадающей с ВНД);
• при вычислении имеет место пренебрежение последовательностью денежных потоков (для формулы не важно, в какой последовательности наступают затраты и приходит прибыль, тогда как на практике это может иметь решающее значение);
• возможны искажения при оценке взаимоисключающих инвестиционных проектов.

Интерпретация внутренней нормы доходности

Главное правило, по которому оценивают возможность инвестирования по показателю ВНД: проект можно принять, если IRR выше, чем средневзвешенная стоимость капитала для компании (WACC). Это значит, что инвестору стоит занимать деньги для вложения, и они, вероятнее всего, принесут добавочную прибыль.

НАПРИМЕР. Банк может предоставить инвестору деньги под 12% годовых. Инвестор собирается взять кредит и вложить средства в проект, ВНД которого 16%. Это значит, что 16% годовых – верхняя планка, по которой можно занять деньги для этого проекта. Если проект действительно принесет 16% прибыли, в пользу инвестора останется 4%, в любом случае он сможет вернуть заемные средства без убытка для себя.

Пример применения ВНД

Приведем жизненный пример оценки внутренней доходности, который может осознать обычный гражданин, а не только предприниматель.

Сдача квартиры в аренду – вроде бы выгодное мероприятие. Но все зависит от того, есть ли эта квартира в собственности. Если это так, то первоначальная инвестиция равна нулю, поэтому проект заведомо рентабелен. Но если планируется вложить средства в покупку квартиры, сдавать ее, а затем продать, чтобы вернуть взятый на это кредит?

Посчитаем, получится ли этот проект выгодным. Пусть квартира стоит 5 млн руб., а сумма аренды за год составит 25 000 руб. в месяц. Пренебрежем налоговыми расходами на оформление покупки квартиры и аренды. За 3 года доход от аренды составит 25 000 х 3 = 75 000 руб. Представим, что конъюнктура рынка недвижимости за 3 года не изменилась и квартиру удастся продать за цену покупки. Значит, спустя три года инвестиция принесет доход 75 000 + 5 млн руб. ВНД такого проекта получится равным приблизительно 6%.

Как известно, ставка кредитования в банке приблизительно составляет 9%, значит, имея в своем распоряжении свободные средства (например, получив их в наследство), их выгоднее положить на депозит, чем покупать квартиру с целью аренды.

Но если стоимость квартиры за эти годы существенно увеличится, ВНД проекта также изменится в лучшую сторону.

Источник

Внутренняя норма доходности IRR

Внутренняя норма доходности — норма прибыли, порожденная инвестицией. Это та норма прибыли (барьерная ставка, ставка дисконтирования), при которой чистая текущая стоимость инвестиции равна нулю, или это та ставка дисконта, при которой дисконтированные доходы от проекта равны инвестиционным затратам. Внутренняя норма доходности определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника.

IRR = r, при котором NPV = f(r) = 0,

Ее значение находят из следующего уравнения:

NPV(IRR) — чистая текущая стоимость, рассчитанная по ставке IRR,
CFt — приток денежных средств в период t;
It — сумма инвестиций (затраты) в t-ом периоде;
n — суммарное число периодов (интервалов, шагов) t = 0, 1, 2, . n.

Определяется: как норма прибыли, при которой чистая текущая стоимость инвестиции равна нулю.

Характеризует: наименее точно, эффективность инвестиции, в относительных значениях.

Синонимы: внутренняя норма прибыли, внутренний коэффициент окупаемости, Internal Rate of Return.

Акроним: IRR

Недостатки: не учитывается уровень реинвестиций, не показывает результат инвестиции в абсолютном значении, при знакопеременных потоках может быть рассчитан неправильно.

Критерий приемлемости: IRR > R бар ef (чем больше, тем лучше)

Условия сравнения: любой срок действия инвестиции и размер.

Экономический смысл данного показателя заключается в том, что он показывает ожидаемую норму доходности (рентабельность инвестиций) или максимально допустимый уровень инвестиционных затрат в оцениваемый проект. IRR должен быть выше средневзвешенной цены инвестиционных ресурсов:

Если это условие выдерживается, инвестор может принять проект, в противном случае он должен быть отклонен.

Достоинства показателя внутренняя норма доходности (IRR) состоят в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

Показатель эффективности инвестиций внутренняя норма доходности (IRR) имеет три основных недостатка.

Во-первых, по умолчанию предполагается, что положительные денежные потоки реинвестируются по ставке, равной внутренней норме доходности. В случае, если IRR близко к уровню реинвестиций фирмы, то этой проблемы не возникает; когда IRR, особенно привлекательного инвестиционного проекта равен, к примеру 80%, то имеется в виду, что все денежные поступления должны реинвестироваться при ставке 80%. Однако маловероятно, что предприятие обладает ежегодными инвестиционными возможностями, которые обеспечивают рентабельность в 80%. В данной ситуации показатель внутренней нормы доходности (IRR) завышает эффект от инвестиций (в показателе MIRR модифицированная внутренняя норма доходности данная проблема устранена).

Во-вторых, нет возможности определить, сколько принесет денег инвестиция в абсолютных значениях (рублях, долларах).

В-третьих, в ситуации со знакопеременными денежными потоками может рассчитываться несколько значений IRR или возможно определение неправильного значения (в программе «Альтаир Инвестиционный анализ 1.хх» эта проблема устранена программным способом, будет и в «Альтаир Инвестиционный анализ 2.01).

Пример №1. Расчет внутренней нормы доходности при постоянной барьерной ставке.
Размер инвестиции — 115000$.
Доходы от инвестиций в первом году: 32000$;
во втором году: 41000$;
в третьем году: 43750$;
в четвертом году: 38250$.
Размер эффективной барьерной ставки — 9,2%.

Решим задачу без использования специальных программ. Используем метод последовательного приближения. Подбираем барьерные ставки так, чтобы найти минимальные значения NPV по модулю, и затем проводим аппроксимацию. Стандартный метод — не устраняется проблема множественного определения IRR и существует возможность неправильного расчета (при знакопеременных денежных потоках). Для устранения проблемы обычно строится график NPV(r)).

Рассчитаем для барьерной ставки равной r_a=10,0%
Пересчитаем денежные потоки в вид текущих стоимостей:
PV₁ = 32000 / (1 + 0,1) = 29090,91$
PV₂ = 41000 / (1 + 0,1) 2 = 33884,30$
PV₃ = 43750 / (1 + 0,1) 3 = 32870,02$
PV₄ = 38250 / (1 + 0,1) 4 = 26125,27$

NPV(10,0%) = (29090,91 + 33884,30 + 32870,02 + 26125,27) — 115000 =
= 121970,49 — 115000 = 6970,49$

Рассчитаем для барьерной ставки равной r_b=15,0%
Пересчитаем денежные потоки в вид текущих стоимостей:
PV₁ = 32000 / (1 + 0,15) 1 = 27826,09$
PV₂ = 41000 / (1 + 0,15) 2 = 31001,89$
PV₃ = 43750 / (1 + 0,15) 3 = 28766,34$
PV₄ = 38250 / (1 + 0,15) 4 = 21869,56$

NPV(15,0%) = (27826,09 + 31001,89 + 28766,34 + 21869,56) — 115000 = 109463,88 — 115000 = — 5536,11$

Делаем предположение, что на участке от точки а до точки б функция NPV(r) прямолинейна, и используем формулу для аппроксимации на участке прямой:

Формула справедлива, если выполняются условия r_a 0 > NPV_b.

Ответ: внутренний коэффициент окупаемости равен 12,7867%, что превышает эффективную барьерную ставку 9,2%, следовательно, проект принимается.

Пример №2. IRR при переменной барьерной ставке.
Размер инвестиции — $12800.
Доходы от инвестиций в первом году: $7360;
во втором году: $5185;
в третьем году: $6270.
Размер барьерной ставки — 11,4% в первом году;
10,7% во втором году;
9,5% в третьем году.
Определите приемлемость проекта по параметру IRR.

Рассчитаем для ставки дисконтирования равной ra=20,0%
Пересчитаем денежные потоки в вид текущих стоимостей:
PV₁ = 7360 / (1 + 0,2) = $6133,33
PV₂ = 5185 / (1 + 0,2)^2 = $3600,69
PV₃ = 6270 / (1 + 0,2)^3 = $3628,47

NPV(20,0%) = (6133,33 + 3600,69 + 3628,47) — 12800 = 13362,49 — 12800 = $562,49

Рассчитаем для ставки дисконтирования равной r_b = 25,0%

Пересчитаем денежные потоки в вид текущих стоимостей:
PV₁ = 7360 / (1 + 0,25) = $5888,00
PV₂ = 5185 / (1 + 0,25)^2 = $3318,40
PV₃ = 6270 / (1 + 0,25)^3 = $3210,24

NPV(25,0%) = (5888,00 + 3318,40 + 3210,24) — 12800 = 12416,64 — 12800 = -383,36

IRR = 20 + (25 — 20)*562,49 / (562,49 — (- 383,36)) = 22,9734%.

Т.к. барьерная ставка переменная, то сравнение производим с эффективной барьерной ставкой.
В соответствии с расчетом примера эффективная барьерная ставка равна 10,895%.

Ответ: внутренний коэффициент окупаемости равен 22,9734%, превышает 10,895%, следовательно, проект принимается.

Правило, согласно которому, из двух проектов, выбирается проект с большим IRR действует не всегда. После учета уровня реинвестиций (пример №3) или барьерной ставки (пример №4) проект с меньшим IRR, может быть выгоднее проекта с большим IRR.

Пример №3. Исключение из правила: выбор проекта с большим значением IRR, влияние уровня реинвестиций барьерной ставки.
Стоимость инвестиции для обоих проектов равна 100 рублям.
Барьерная ставка равна 12%.
Уровень реинвестиций постоянный и равен 10%.
Первый проект генерирует прибыль равную 200 рублей по окончании 1 года и 100 рублей по окончании второго года, а второй генерирует прибыль равную 160 рублей в течении первых 3 лет и затем по 60 рублей еще 4 года.
Сравните два проекта.

Рассчитаем значения параметров IRR и MIRR для каждого из проектов:
IRR₁ = 141,42%.
IRR₂ = 153,79%.
MIRR₁ = 73,205%.
MIRR₂ = 40,0%.
Но при этом годовая доходность, рассчитанная по модели MIRR будет у первого проекта равна 73,205%., а у второго всего лишь 40,0%, несмотря на больший IRR. Т.к. расчет по модели MIRR точнее чем IRR то примут первый инвестиционный проект (если рассматривать только с точки зрения финансовой эффективности).

Пример №4. Исключение из правила: выбор проекта с большим значением IRR, влияние барьерной ставки.
Стоимость инвестиции для обоих проектов равна 100 рублям.
Барьерная ставка равна 25%.
Первый проект генерирует прибыль равную 160 рублей по окончании 1 года, а второй генерирует прибыль равную 80 рублей в течении 7 лет.
Сравните два проекта.

IRR₁ = 60,0%.
IRR₂ = 78,63%.
Т.к. срок действия инвестиционных проектов существенно различается, то сравнивать по параметру DPI не представляется возможным; сравниваем по MIRR(бар) и с NRR в годовых значениях.
MIRR(бар)₁ = 60,0%
MIRR(бар)₂ = 42,71%
Чистая доходность NRR₁, годовых = 28%.
Чистая доходность NRR₂, годовых = 21,84%.

Показатели MIRR(бар) и NRR, % годовых больше у первого проекта, несмотря на меньший IRR.

Пример №5. Анализ чувствительности.
Размер инвестиции — $12800.
Доходы от инвестиций в первом году: $7360;
во втором году: $5185;
в третьем году: $6270.
Определите, как повлияет на значение внутренней нормы доходности увеличение прибыли от инвестиции на 23,6%.

Исходная внутренняя норма доходности была рассчитана в примере №2 и равна IRR_исх = 22,97%.
Определим значение денежных потоков с учетом увеличения их на 23,6%.
CF_{1 ач} = 7360 * (1 + 0,236) = $9096,96
CF_{2 ач} = 5185 * (1 + 0,236) = $6408,66
CF_{3 ач} = 6270 * (1 + 0,236) = $7749,72

Рассчитаем для ставки дисконтирования равной r_a = 30,0%
Пересчитаем денежные потоки в вид текущих стоимостей:
PV_{1 ач} = 9096,96 / (1 + 0,3) 1 = $6997,661
PV_{2 ач} = 6408,66 / (1 + 0,3) 2 = $3792,106
PV_{3 ач} = 7749,72 / (1 + 0,3) 3 = $3527,410
NPV_ач(30,0%) = (6997,661 + 3792,106 + 3527,410) — 12800 = 13 593,118 — 12800 = $793,1180

Рассчитаем для ставки дисконтирования равной r_b = 40,0%
Пересчитаем денежные потоки в вид текущих стоимостей:
PV_{1 ач} = 9096,96 / (1 + 0,4) 1 = $6497,828
PV_{2 ач} = 6408,66 / (1 + 0,4) 2 = $3269,724
PV_{3 ач} = 7749,72 / (1 + 0,4) 3 = $2824,242
NPV_ач(40,0%) = (6497,828 + 3269,724 + 2824,242) — 12800 = 12 591,794 — 12800 = — $208,206

IRR_ач = 30 + (40 — 30) * 793,118 / (793,118 — (- 208,206)) = 37,92%.

Определим изменение внутренней нормы доходности: (IRR_ач — IRR_исх) / IRR_исх * 100% = (37,92 — 23,6)/23,6*100% = 60,68%.

Ответ. Увеличение размера доходов на 23,6% привело к увеличению внутренней нормы доходности на 60,68%.

Примечание. Дисконтирование денежных потоков при меняющейся во времени барьерной ставке (норме дисконта) соответствует «Методическим указаниям № ВК 477 . » п.6.11 (стр. 140).

Главная Методики финансового и инвестиционного анализа Инвестиционный анализ Внутренняя норма доходности

Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.

Источник