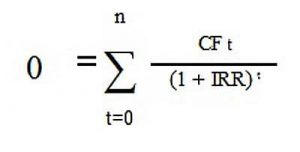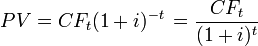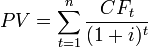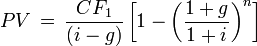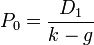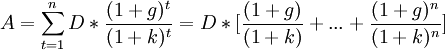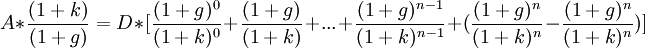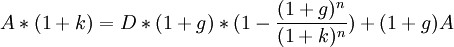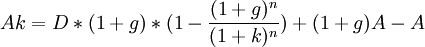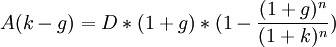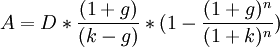- Расчет внутренней нормы доходности
- Что такое внутренняя норма доходности?
- Показатели для расчета IRR
- Формула расчета внутренней нормы рентабельности
- Способы вычисления ВНД
- Достоинства и недостатки метода IRR
- Интерпретация внутренней нормы доходности
- Пример применения ВНД
- Вопрос 2. Чистый денежный поток, приведенная (дисконтированная) стоимость, внутренняя норма доходности.
Расчет внутренней нормы доходности
Ни один инвестор не вкладывает средства слепо, не проведя предварительных исследований: он должен быть уверен, что они окупятся или, как минимум, их удастся вернуть. Для этого оценивается потенциальная рентабельность инвестиционного проекта. Конечно, это нельзя сделать иначе как комплексно, применяя ряд специально разработанных показателей, важнейший из которых – внутренняя норма доходности.
Рассмотрим, в чем особенности метода инвестиционных исследований, основанного на вычислении внутренней нормы доходности – IRR.
Что такое внутренняя норма доходности?
Никто не может рассчитать с вероятностью 100%, какой доход удастся получить от вложенных средств. Слишком много переменных факторов, могущих повлиять на реализацию бизнес-проекта, профинансированного инвестором. Однако можно максимально снизить риск неточностей, если применить не абсолютную, а относительную оценку.
Та процентная ставка, при которой инвестор гарантированно возместит свое вложение, но не получит прибыли, называется внутренней нормой доходности (ВНД). Норма заключается в том, что все денежные потоки данного инвестиционного проекта в сумме взаимозачтутся. Иначе говоря, расходы на инвестиционный проект в какой-то момент времени уравновешиваются полученными доходами (говорят, что проект «вышел в ноль»).
ВАЖНО! Слово «внутренняя» в определении данной нормы инвестиционных вложений означает ее зависимость от свойств самого проекта, а не от внешних факторов.
Внутреннюю норму доходности специалисты могут именовать по-разному. Встречаются следующие наименования:
- ВНД – русская аббревиатура;
- IRR – английская аббревиатура от «Internal Rate of Return» – «внутренняя норма доходности»;
- внутренняя норма рентабельности;
- внутренняя норма прибыли;
- внутренняя норма возврата инвестиций;
- предельная эффективность капитальных вложений;
- процентная норма прибыли;
- дисконтированный поток реальных денег;
- финансовая норма прибыли;
- собственная норма прибыли.
ВНИМАНИЕ! Эту норму можно счесть предельной, поскольку выход за ее пределы уже означает для инвестора убыток.
Показатели для расчета IRR
Математически расчет внутренней нормы доходности не так уж сложен, но формула включает много дополнительных показателей, которые необходимо учитывать. Среди них:
- NPV – от первых букв выражения «Net Present Value» («чистая приведенная стоимость») – сумма всех денежных потоков данного проекта, приведенная к общему показателю при взаимозачете доходов и затрат;
- CF – денежные потоки (от «Cash Flows») – величины различных притоков и оттоков финансов, в том числе и инвестируемых средств, в выбранный период времени t (обычно берется год). Для инвестиционного проекта первый денежный поток – сама инвестиция – естественно, будет иметь отрицательное значение (это затрата).
- R – ставка дисконтирования, то есть тот процент, под который инвестор может получить средства для вложений (взять банковский кредит, продать свои акции или использовать внутренние средства).
- WACC – средневзвешенная стоимость капитала (от Weighted Average Cost of Capital) – если применяется сразу несколько источников привлечения денег, то процентная ставка будет представлять среднюю величину, рассчитанную пропорционально.
ВАЖНАЯ ИНФОРМАЦИЯ! Было бы очень просто рассчитать внутреннюю норму доходности, зная все необходимые показатели. Однако на практике невозможно определить точные величины денежных потоков и однозначно вычислить ставку дисконтирования. Поэтому для каждого отдельного проекта оценивают степень зависимости NPV от процентной ставки.
Формула расчета внутренней нормы рентабельности
IRR – это такая величина R, при которой NPV равен нулю. Поэтому этот показатель можно вывести из формулы расчета приведенной суммы денежных потоков.
- 0 означает величину NPV;
- n – количество исследуемых временных периодов;
- CFt – денежные потоки в учетный момент времени.
Способы вычисления ВНД
Посчитать значение внутренней нормы доходности вручную не представляется возможным, так как, если вывести из него значение IRR, оно получится множителем 4 степени. Вычислить этот показатель можно несколькими способами:
- использовать специальный финансовый калькулятор;
- применить программу Excel, в которой эта функция встроена в раздел «Финансовые формулы» под названием ВСД («внутренняя ставка доходности»);
- воспользоваться одним из онлайн-калькуляторов;
- применить графический способ (использовался до широкого распространения Персональных компьютеров).
Достоинства и недостатки метода IRR
Для оценки инвестиционных возможностей главным образом применяются два метода – вычисление NPV и IRR. Метод определения внутренней нормы доходности относителен, поэтому не может претендовать на высокую точность, однако обладает рядом преимуществ:
- помогает достаточно просто оценить рентабельность инвестиционного проекта;
- показывает максимально допустимый размер затрат для вложения в проект;
- позволяет сравнивать различные проекты по рентабельности, даже если они отличаются по масштабу и протяженности во времени.
Недостатки метода IRR:
- нельзя посчитать абсолютную доходность инвестиции (то есть сколько конкретно денег – рублей, валюты – она может принести инвестору);
- возможно завышение инвестиционного эффекта, если ВНД сильно отличается от уровня реинвестиций компании (то есть положительные денежные потоки «возвращаются» инвестору с процентной ставкой, не совпадающей с ВНД);
- при вычислении имеет место пренебрежение последовательностью денежных потоков (для формулы не важно, в какой последовательности наступают затраты и приходит прибыль, тогда как на практике это может иметь решающее значение);
- возможны искажения при оценке взаимоисключающих инвестиционных проектов.
Интерпретация внутренней нормы доходности
Главное правило, по которому оценивают возможность инвестирования по показателю ВНД: проект можно принять, если IRR выше, чем средневзвешенная стоимость капитала для компании (WACC). Это значит, что инвестору стоит занимать деньги для вложения, и они, вероятнее всего, принесут добавочную прибыль.
НАПРИМЕР. Банк может предоставить инвестору деньги под 12% годовых. Инвестор собирается взять кредит и вложить средства в проект, ВНД которого 16%. Это значит, что 16% годовых – верхняя планка, по которой можно занять деньги для этого проекта. Если проект действительно принесет 16% прибыли, в пользу инвестора останется 4%, в любом случае он сможет вернуть заемные средства без убытка для себя.
Пример применения ВНД
Приведем жизненный пример оценки внутренней доходности, который может осознать обычный гражданин, а не только предприниматель.
Сдача квартиры в аренду – вроде бы выгодное мероприятие. Но все зависит от того, есть ли эта квартира в собственности. Если это так, то первоначальная инвестиция равна нулю, поэтому проект заведомо рентабелен. Но если планируется вложить средства в покупку квартиры, сдавать ее, а затем продать, чтобы вернуть взятый на это кредит?
Посчитаем, получится ли этот проект выгодным. Пусть квартира стоит 5 млн руб., а сумма аренды за год составит 25 000 руб. в месяц. Пренебрежем налоговыми расходами на оформление покупки квартиры и аренды. За 3 года доход от аренды составит 25 000 х 3 = 75 000 руб. Представим, что конъюнктура рынка недвижимости за 3 года не изменилась и квартиру удастся продать за цену покупки. Значит, спустя три года инвестиция принесет доход 75 000 + 5 млн руб. ВНД такого проекта получится равным приблизительно 6%.
Как известно, ставка кредитования в банке приблизительно составляет 9%, значит, имея в своем распоряжении свободные средства (например, получив их в наследство), их выгоднее положить на депозит, чем покупать квартиру с целью аренды.
Но если стоимость квартиры за эти годы существенно увеличится, ВНД проекта также изменится в лучшую сторону.
Источник
Вопрос 2. Чистый денежный поток, приведенная (дисконтированная) стоимость, внутренняя норма доходности.
Чистый денежный поток – разность между суммами поступлений и выплат денежных средств компании за определенный период времени. Чистый денежный поток рассчитывается с учетом выплат, дивидендов и налогов.
Понятие чистого денежного потока (Net Cash Flow, NCF) используется при оценке эффективности инвестиций. Это суммарный поток, включающий все платежи проекта, кроме платежей, связанных с притоком и оттоком капитала (при этом, например, проценты по кредитам включаются в NCF, т.к. это затраты на обеспечение проекта, а дивиденды – не включаются, т.к. это изъятие части капитала владельцами бизнеса).
В некоторых случаях, в зависимости от целей расчетов, начальные инвестиции также не включают в NCF, тогда чистый денежный поток состоит только из разности текущих поступлений и затрат, связанных с реализацией инвестиционного проекта.
Чистые денежные поступления (ЧДП), или чистый денежный поток, которые остаются у предприятия после уплаты налогов, можно в общем виде рассчитать по формуле
где П — приток денежных средств;
О — отток денежных средств.
Рис. 3.3. Схема притоков и оттоков денежных средств предприятия
Чистые денежные поступления от хозяйственной деятельности (ЧДП0) можно выразить уравнением
ЧДП0 = Вр — (И — А) — Н — Пр , (3.2)
где Вр — выручка от реализации продукции;
И — издержки производства и сбыта;
Пр — выплаты процентов по кредитам.
Амортизация по своей экономической природе, являясь отчислением, призванным обеспечить накопление средств для компенсации износа основного капитала, не перестает быть собственностью предприятия, хотя и вычитается из его прибыли. Поэтому вполне логично включать начисленную амортизацию в денежный поток (денежные поступления).
Чистый дисконтированный доход (чистая приведённая стоимость) (англ. Net present value, общепринятое сокращение — NPV (ЧДД)) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.
Иначе говоря, для потока платежей CF, где CFt — платёж через t лет (t = 1. N) и начальной инвестиции в размере IC = − CF0 чистый дисконтированный доход NPV рассчитывается по формуле:
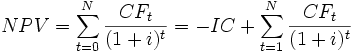
где i — ставка дисконтирования.
Расчёт ЧДД — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧДД больше 0, то инвестиция прибыльна, а если ЧДД меньше 0, то инвестиция убыточна.
С помощью ЧДД можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧДД).
В отличие от показателя дисконтированной стоимости при расчете чистого дисконтированного дохода не учитывается начальная инвестиция. Поэтому формула чистого дисконтированного дохода отличается от формулы дисконтированной стоимости на величину начальной инвестиции IC = − CF0.
Достоинства и недостатки
Положительные качества ЧДД:
— чёткие критерии принятия решений
— показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).
Отрицательные качества ЧДД: показатель не учитывает риски.
Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчетный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события.
Дисконтированная стоимость выражает стоимость будущих потоков платежей в значении текущих потоков платежей. Определение дисконтированной стоимости широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить какой объем финансовых вложений намерен сделать инвестор для получения определенного денежного потока через заданный срок. Дисконтированная стоимость будущего потока платежей является функцией:
— срока через который ожидается будущий поток платежей,
— риска связанного с данным будущим потоком платежей,
— стоимости денег с учетом фактора времени
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену вследствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб. которые будут получены через пять лет.
где 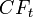
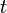
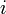
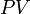
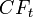
Для того чтобы получить через 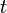
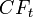
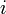
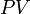
В табличных процессорах в состав финансовых функций входит функция для вычисления дисконтированной стоимости. В OpenOffice.org Calc для вычисления дисконтированной стоимости различных видов платежей применяется функция PV.
Дисконтированная стоимость серии потоков платежей и аннуитетных платежей
Дисконтированная стоимость серии потоков платежей равна сумме дисконтированных стоимостей каждого из составляющих потоков платежей. Так, дисконтированная стоимость серии потоков платежей 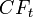
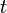
Если аннуитетные платежи имеют одинаковую величину, то эту формулу можно применять и для вычисления дисконтированной стоимости аннуитетных платежей.
Для большого 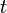
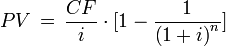
где 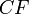
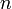
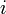
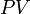
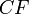
Дисконтированная стоимость аннуитетных платежей с ростом
Если денежные потоки аннуитетных платежей растут в (1+g) раз (ставка роста равна g), то их дисконтированная стоимость вычисляется по формуле:
где 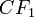
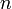
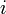
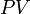
Формула получается вычитанием формулы для расчета дисконтированной стоимости перпетуитета начинающегося в году n из упрощенной формулы модели Гордона.
Дисконтированная стоимость перпетуитетов (бессрочных аннуитетов)
Исходя из формулы расчета дисконтированной стоимости аннуитетных платежей, можно получить формулу для дисконтированной стоимости перпетуитетов(бессрочных аннуитетов). Когда значение 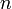
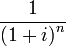
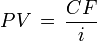
Дисконтированная стоимость бессрочных ценных бумаг с растущими платежами, например акции c увеличивающимися дивидендными доходами рассчитывается по модели Гордона
Модель Гордона является вариацией модели дисконтирования дивидендов, методом для вычисления цены акции или бизнеса. Данная модель часто используется для оценки стоимости внебиржевых компаний, которую сложно оценить другими методами.
Модель подразумевает, что компания на сегодняшний день выплачивает дивиденды в размере D, которые в будущем будут увеличиваться с неизменной ставкой g. Также подразумевается, что требуемая процентная ставка (ставка дисконтирования) акции остается постоянной на уровне k.
Тогда текущая цена акции будет равна:
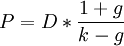
На практике P часто корректируется с учетом различных факторов, например, размера компании. Распространено использование упрощенного вида формулы
где D1 — дивиденд будущего года D1 = D0(1 + g).
Цену акции можно определить методом дисконтирования в следующем виде: 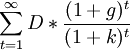
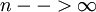
Для определения внутренней нормы доходности облигации часто используют приближённую «купеческую» формулу: 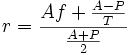
A — номинал облигации;
P — текущая рыночная цена облигации;
f — годовая купонная ставка;
T (в годах) — срок до погашения облигации.
Связь способа расчета внутренней нормы доходности с показателем дисконтированной стоимости состоит в том, что показатель внутренней нормы доходности отражает тот уровень ставки дисконтирования, при которой дисконтированная стоимость полученных доходов за вычетом суммы первоначальной инвестиции (чистая дисконтированная стоимость) будет равна нулю. Чем выше должна быть ставка дисконтирования для приведения чистой дисконтированной стоимости полученных доходов к нулю, тем предпочтительнее данная инвестиция.
Показатель внутренней нормы доходности основывается на допущении, что денежные потоки, полученные до погашения инвестиции (истечения срока ее действия), будут реинвестированы по ставке, равной внутренней норме доходности, и что она останется неизменной.
Инвестиция считается приемлемой, если внутренняя норма доходности выше, чем минимальный приемлемый показатель окупаемости инвестиций в финансовый инструмент. Такие инвестиции представляют интерес для инвестора.
Показатель внутренней нормы доходности для облигаций называется доходностью к погашению. Доходность к погашению облигации может отличаться от купонной ставки, если облигация продается по цене, отличающейся от номинальной стоимости.
Дата добавления: 2015-11-06 ; просмотров: 3423 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник