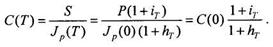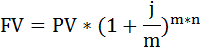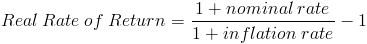Расчет ставки реальной доходности с учетом инфляции

1.ТЕОРИЯ ПРОЦЕНТОВ

1.6. Реальная ставка доходности с учетом инфляции и налогообложения

Инфляция — это снижение реальной покупательной способности денег. В чисто финансовых расчетах, где фигурируют только изменения номинальных денежных сумм, этот фактор не учитывается. В реальности далеко не всякая ставка доходности может привлечь внимание инвесторов. Очевидно, что при темпе инфляции 50% в год едва ли кто будет вкладывать деньги под меньший процент. Такое интуитивное понимание ситуации следует дополнить количественным анализом, призванным ответить на вопрос: какова же реальная доходность инвестиций с учетом темпов инфляции?

Прежде всего, необходимо ввести измеритель уровня и темпов инфляции. Стоимость инвестиций и уровня доходов разных лет может быть сопоставима только в том случае, если стоимость денежной единицы не изменяется. Уровень инфляции выражается в виде индекса цен. Индекс цен является измерителем соотношения между совокупной ценой определенного набора товаров и услуг, называемых «рыночной корзиной», для данного временного периода и совокупной ценой идентичной либо сходной группы товаров и услуг в базовом периоде:

(1.5.1)

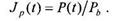
федеральное правительство США рассчитывает индексы различных наборов, или «корзин», товаров и услуг. Наиболее известный из них — индекс потребительских цен (ИПЦ) — цена фиксированной корзины, содержащей 300 потребительских товаров и услуг, покупаемых типичным горожанином. Индекс цен валового национального продукта, или дефлятор ВНП, включает не только цены потребительских товаров и услуг, но также и цены инвестиционных товаров, товаров, покупаемых правительством, а также товаров и услуг, купленных и проданных на мировом рынке. В зависимости от характера задачи используется тот или иной индекс цен.

Темпом инфляции за определенный период Т называют относительное изменение индекса цен за этот период

(1.5.2)

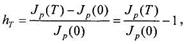
Если известны индекс цен в начале периода и прогнозируемый темп инфляции за период, то можно вычислить ожидаемый индекс цен в конце периода:

(1.5.3)

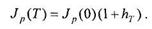
Полученное значение индекса цен будет исходным для вычислений в следующем периоде:

(1.5.4)

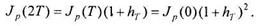
По прошествии т периодов индекс цен будет равен

(1.5.5)

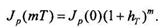
Темп инфляции за этот интервал времени в соответствии (1.5.2) равен

(1.5.6)

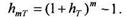
Из формулы (1.5.5) видно, что возрастание индекса цен аналогично наращению денежных сумм по закону сложных процентов. Если известен темп инфляции за какую-либо l/m-ю часть года, то годовой темп инфляции в соответствии с (1.5.6) определяется формулой

(1.5.7)

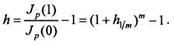
Реальная ставка доходности и инфляционная премия

Инфляционное обесценение денег существенно снижает реальную доходность финансовой операции. Под реальной доходностью финансовой операции мы понимаем относительное приращение за период Т реальной покупательной способности С денежной суммы, равной отношению этой суммы к индексу цен в данный момент времени:

(1.5.8)

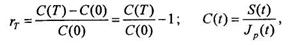
Покупательная способность наращенной за период суммы Р равна

Подставляя это выражение в (1.5.8), получим формулу, выражающую реальную доходность через процентную ставку и темп инфляции:

(1.5.9)

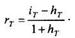
Если период Т равен одному году, то нижний индекс у переменных опускают: h — годовой темп инфляции, r — реальная годовая ставка доходности.

Формула (1.5.9) опровергает распространенное заблуждение, что будто бы для получения реальной ставки доходности достаточно из процентной ставки вычесть темп инфляции; это справедливо только при очень малой величине темпа инфляции, когда величиной h в знаменателе можно пренебречь по сравнению с единицей.

Формула (1.5.9) удобна для демонстрации снижения доходности инвестиций в условиях инфляции, показывающей вели чину реальной доходности при заданной процентной ставке. На практике же обычно задаются минимальной приемлемой для инвестора величиной реальной доходности (барьерной ставкой) r, исходя из которой определяют минимальную процентную ставку i, под которую еще имеет смысл инвестировать средства:

(1.5.10)

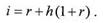
Формула (1.5.10) носит название формулы Фишера. Вторе слагаемое в правой части этой формулы – величина, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина носит название инфляционной премии. Пусть барьерная ставка равна 15% годовых при темпе инфляции, определенном в примере 1.5.2 тогда приемлемая величина процентной ставки будет равна 0,15+0,426х(1+0,15)=0,64 (64%). Из примера 1.5.2 видно, что реальная ставка доходности почти в 5 раз ниже годовой процентной ставки – впечатляющий результат!

Реальная ставка доходности с учетом налога

Вопрос о налогообложении прибыли от инвестирования средств приобретает особую важность, ведь налог начисляется не с реального дохода, а с номинального, равного приращению денежной суммы, и величина налога может оказаться больше реального дохода! Пусть ставка налога на прибыль равна g тогда чистая прибыль, т.е. прибыль после уплаты налога, равна iP—iPg=Pi(1-g). Отсюда видно, что учет налога на прибыль сводится к замене процентной ставки i на ставку i_g=i/(l-g).

Формула для реальной доходности с учетом налога на прибыль примет вид

(1.5.11)

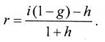
Определим приемлемую процентную ставку с учетом налогообложения, преобразуя формулу (1.5.11):

(1.5.12)

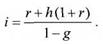
Источник

Задача №33. Расчёт реального дохода вкладчика с учётом инфляции

Вклад в сумме 35000 руб. положен в банк на год с ежемесячным исчислением сложных процентов; годовая ставка по вкладам 6%; уровень инфляции за месяц 10%.

Определить:

а) сумму вклада с процентами (FV),

б) индекс инфляции за 6 месяцев (I_n),

в) сумму вклада с процентами с точки зрения её покупательной способности (K_r),

г) реальный доход вкладчика с точки зрения покупательной способности (d).

Решение:

а) Сумму вклада рассчитаем по формуле наращения по сложным процентам:

FV – наращенная сумма вклада,

PV – настоящая стоимость денег,

n – срок операции,

m – число раз начисления процентов в году,

j – годовая (номинальная) ставка, выраженная десятичной дробью,

j/m – процентная ставка за период

FV = 35000 * (1 + 0,06 / 12) 12*1 = 37158,72 руб.

б) Индекс инфляции за 12 месяцев найдём по формуле:

I_n = (1 + 0,1) 12 = 3,1384.

в) Сумму вклада с процентами с точки зрения её покупательной способности (K _r ) найдём как отношение наращенной суммы вклада (FV) к индексу инфляции (I_n):

K_r = FV / I_n = 37158,72 / 3,1384 = 11839,91 руб.

г) Реальный доход вкладчика с точки зрения покупательной способности (d) вычислим так:

d = K_r – PV = 11839,91 – 35000 = – 23160,09 (реальный убыток).

Источник

Геометрическая разница, считаем реальную доходность

В прошлой публикации Где интуиция не срабатывает: считаем доходность мы рассказывали об алгебраической и геометрической суммах. Речь шла о том, как правильно считать доходность.

Когда мы употребляем термин доходность, то в большинстве случаев имеется ввиду номинальная доходность, то есть без учета инфляции. Как правило, инвестора интересует реальная доходность с учетом влияния инфляции.

Как и в прошлой статье начнем с простого примера. Если доходность депозита составила 18% годовых, а инфляция за тот же период — 11%, какова итоговая доходность?

Проверьте себя. Как бы вы посчитали результат?

Что случится, если вдруг инфляция в этот год взлетит до 118%?

Довольно часто в первом случае люди полагают, что Реальная доходность составила 7%:

Такое вычитание называется алгебраическим.

Работает ли алгебраическое вычитание во втором случае?

Может ли реальная доходность достигать -100% после учета инфляции? Это значило бы, что покупательная сила денег стала равной нулю. А если инфляция составила бы 120%, мы потеряли бы больше денег, чем у нас было? Вряд ли такой метод вычитания может быть правильным …

Как и раньше, помогает геометрическая разница:

При расчете процентные соотношения переводятся в десятичные дроби, хотя в EXCEL можно этого не делать. EXCEL умеет сам переводить из дробей в проценты и наоборот (см. прилагаемый файл).

Обобщаем

Если доходность составила R процентов, а инфляция равняется N, то реальная доходность вычисляется по формуле:

Всегда ли неправильно считать доходность через алгебраическую сумму?

В примере, когда номинальная доходность составила 18% а инфляция – 11%, можно заметить, что результаты алгебраического и геометрического вычитания довольно близки. Ошибка составит лишь 0,69%.

Действительно, иногда полезно пользоваться алгебраической разницей для получения приближенных результатов. Ошибка будет незначительной в тех случаях, когда инфляция и доходность не слишком сильно отличаются.

Тем не менее, когда рассматриваются доходности за несколько периодов или когда разница между номинальной доходностью и инфляцией значительна, величина ошибки возрастает.

Источник

Как правильно рассчитать реальную доходность с учетом инфляции

Многим известно, что инфляция негативно влияет на доходность инвестиции. Но не все умеют правильно рассчитывать реальную доходность с учетом инфляции.

Сначала определимся, что является доходностью.

Деньги обладают покупательной способностью. То есть в будущем на одну и ту же сумму сможете купить меньшее количество товаров и услуг. Покупательная способность денег определяется инфляцией.

Поэтому есть два варианта доходности:

• Номинальная доходность — рассчитанная без поправки на инфляцию.
• Реальная доходность — рассчитанная с поправкой на инфляцию, то есть с учетом будущей покупательной способности денег в сегодняшних ценах.

Как рассчитать реальную доходность?

Я заметил, что многие считают этот показатель по простой формуле:

Реальная доходность = Номинальная доходность — Инфляция

Но этот способ неточен. Причем, чем выше инфляция, тем точность все ниже.

Пример 1️⃣

Инфляция — 4% (сколько примерно она составила за 2020 год в России), а номинальная доходность — 15%.

По данной формуле реальная доходность составляет:

Это близко к истине, но не точно.

Пример 2️⃣

Инфляция — 120%, а номинальная доходность — 20%.

Сколько составит реальная доходность?

20% — 120% = -100%. Нет, такого быть не может.

Правильная формула для расчета:

Реальная доходность за год = (1 + номинальная доходность за год) / (1 + инфляция) — 1.

Давайте пересчитаем наши примеры:

Пример 1️⃣

Инфляция — 4%, а номинальная доходность — 15%

Реальная доходность за год = (1 + 15%) / (1 + 4%) — 1 = 10,6%.

А не 11%, как по первой формуле.

Пример 2️⃣

Инфляция — 120%, а номинальная доходность — 20%.

Реальная доходность за год = (1 + 20%) / (1 + 120%) — 1 = -45%.

А не -100%, как по первой формуле.

Надеюсь, понятно объяснил 🙂.

Считаете для себя реальную доходность?

Источник

Как правильно считать реальную доходность с учетом инфляции?

Автор: Алексей Мартынов · Опубликовано 03.07.2015 · Обновлено 02.12.2018

Наверно все знают, что реальная доходность — это доходность за вычетом инфляции. Все дорожает — продукты, товары, услуги. По данным Росстата за последние 15 лет цены выросли в 5 раз. Это означает, что покупательная способность денег, просто лежавших все это время в тумбочке уменьшилась в 5 раз, раньше могли купить 5 яблок, теперь 1.

Чтобы хоть как-то сохранить покупательную способность своих денег, люди их вкладывают в различные финансовые инструменты: чаще всего это депозиты, валюта, недвижимость. Более продвинутые используют, акции, ПИФы, облигации, драгметаллы. С одной стороны сумма вложений растет, с другой происходит их обесценивание из-за инфляции. Если из номинальной ставки доходности вычесть ставку инфляции, получится реальная доходность. Она может быть положительной или отрицательной. Если доходность положительная, ваши вложения приумножились в реальном выражении, то есть вы можете купить больше яблок, если отрицательная — обесценились.

Большинство инвесторов считают реальную доходность по простой формуле:

Но данный способ неточен. Приведу пример: возьмем 200 рублей и положим их на депозит на 15 лет со ставкой 12% годовых. Инфляция за этот период 7% в год. Если считать реальную доходность по простой формуле, то получится 12-7=5%. Проверим этот результат, посчитав на пальцах.

За 15 лет при ставке 12% годовых 200 рублей превратятся в 200*(1+0,12)^15=1094,71. Цены за это время вырастут в (1+0,07)^15=2,76 раз. Чтобы посчитать реальную доходность в рублях делим сумму на депозите на коэффициент инфляции 1094,71/2,76=396,63. Теперь, чтобы перевести реальную доходность в проценты считаем (396,63/200)^1/15 -1 *100% = 4,67%. Это отличается от 5%, то есть проверка показывает, что расчет реальной доходности «простым» способом не точен.
Чтобы правильно рассчитать реальную доходность, нужно применять формулу:

Real Rate of Return — реальная доходность
nominal rate — номинальная ставка доходности
inflation rate — инфляция

Проверяем:
(1+0,12)/(1+0,07)-1 * 100%=4,67% Сходится, значит формула верная.

Еще одна формула, которая дает тот же результат, выглядит так:

Источник