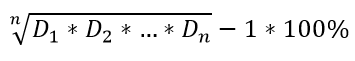- Курс лекций «Основы финансового менеджмента»
- Как считать доходность инвестиций: формулы расчета
- Как рассчитать доходность инвестиций?
- Как считать доходность в процентах годовых?
- Как считать среднегодовую доходность
- Как рассчитать среднюю годовую доходность, если известны доходности по годам?
- Как рассчитать рентабельность проекта: формула и примеры
- Название показателя
- Формула расчета
- Вариант 1. Расчет по средней стоимости вложений
- Вариант 2. Расчет с учетом остаточной стоимости имущества
- Вариант 3. Расчет по размеру первоначальных инвестиций
- Значение показателя в бизнес-планировании
- Преимущества и недостатки
Курс лекций «Основы финансового менеджмента»
5.2. Определение средней доходности
В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

n – число видов финансовых инструментов в портфеле;
r i – доходность i -го инструмента;
w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.
Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).
В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.
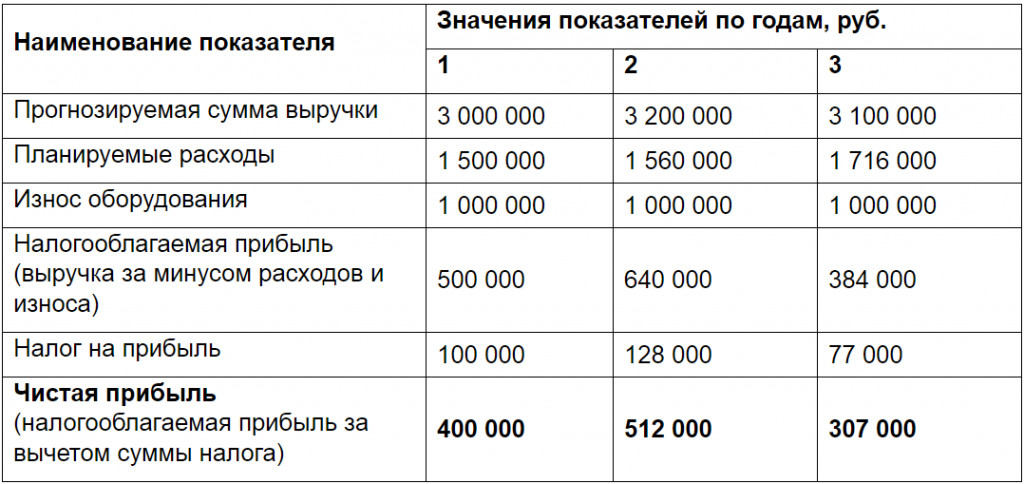
Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).
Таблица 5.2.1
Динамика доходности акции за 3 года
руб.
Источник
Как считать доходность инвестиций: формулы расчета
Автор: Алексей Мартынов · Опубликовано 01.06.2015 · Обновлено 05.11.2015

Доходность (норма доходности, уровень доходности) — это степень увеличения (или уменьшения) инвестированной суммы за определенный период времени. В отличие от дохода, который выражается в номинальных величинах, то есть в рублях, долларах или евро, доходность выражается в процентах. Доход можно получать в двух видах:
- процентный доход — это проценты по депозитам, купоны по облигациям, дивиденды по акциям, арендная плата по недвижимости;
- рост стоимости купленных активов — когда цена продажи актива больше цены покупки — это акции, облигации, недвижимость, золото, серебро, нефть и другие товарные активы.
Такие активы как недвижимость, акции и облигации могут сочетать в себе два источника дохода. Расчет доходности нужен для оценки роста или падения вложений и является критерием оценки эффективности инвестиций.
Как рассчитать доходность инвестиций?
В общем виде доходность всегда рассчитывается как прибыль (или убыток), деленная на сумму вложенных средств, умноженная на 100%. Прибыль считается как сумма продажи актива — сумма покупки актива + сумма денежных выплат, полученных за период владения активом, то есть процентный доход.
Формула 1
Мы купили акцию по цене 100 рублей (сумма вложений), продали акцию по цене 120 рублей (сумма продажи), за период владения акцией получили 5 рублей дивидендов (денежные выплаты). Считаем доходность: (120-100+5)/100 = 0,25 ∗ 100% = 25%.
Формула 2
Есть вторая формула, по которой доходность считается как сумма продажи актива + сумма денежных выплат, деленная на сумму вложений, минус 1, умноженная на 100%.
Как считать доходность в процентах годовых?
В формуле расчета простой доходности не учитывается такой важный параметр, как время. 25% можно получить за месяц, а можно и за 5 лет. Как тогда корректно сравнить доходность активов, время владения которыми различается? Для этого считают доходность в процентах годовых. Доходность в процентах годовых рассчитывается для того, чтобы сравнить друг с другом эффективность активов, время владения которыми отличается. Доходность в процентах годовых — это доходность, приведенная к единому знаменателю — доходности за год.
К примеру банковский вклад дает 11% в год, а какие-то акции принесли 15% за 1,5 года владения ими, что было выгоднее? На первый взгляд акции, они ведь принесли доходность больше. Но инвестор владел ими больше на полгода, поэтому их доходность как бы растянута во времени по сравнению с депозитом. Поэтому, чтобы корректно сравнить депозит и акции, доходность акций нужно пересчитать в процентах годовых.
Для этого в формулу добавляется коэффициент 365/T, где Т — количество дней владения активом.
Мы купили акцию за 100 рублей, продали через 1,5 года за 115 рублей. 1,5 года это 1,5*365=547 дней.
(115-100)/100 ∗ 365/547 ∗ 100% = 10%. В этом случае депозит оказался немного выгоднее акций.
Как форекс, управляющие компании, брокеры и банки манипулируют годовой доходностью.
В любой рекламе доходности обращайте внимание на сноски, уточняйте какую доходность указывают в рекламе и за какой период. К примеру, в рекламе звучит доходность 48% годовых. Но она может быть получена всего лишь за один месяц. То есть компания за месяц заработала 4% и теперь с гордостью рекламирует продукт, дающий 4*12=48% годовых. Даже вы, заработав за день на бирже 1%, можете хвастаться, что заработали 365% годовых) Только доходность эта виртуальная.
 Как считать среднегодовую доходность
Как считать среднегодовую доходность
Срок владения активами может составлять несколько лет. При этом большинство активов не растет на одну и ту же величину. Такие активы как акции могут падать или расти на десятки или сотни процентов в год. Поэтому хочется знать, сколько в среднем в год росли ваши инвестиции. Как тогда вычислить среднюю годовую доходность? Среднегодовая доходность рассчитывается через извлечение корня по формуле:
Формула 1
где n — количество лет владения активом.
3√125/100 — 1 ∗ 100% = 7,72%
Формула 2
Другая формула расчета среднегодовой доходности — через возведение в степень.

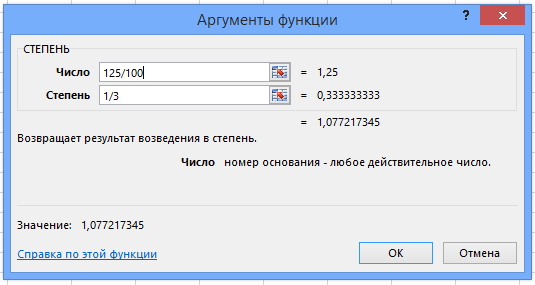
Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Если известны доходности актива по годам, то среднюю годовую доходность можно вычислить перемножив годовые доходности и извлечь из произведения корень в степени равной количеству лет.
Для начала переведите доходности из процентов в числа.
Эти формулы учитывают эффект сложных процентов. Простая формула расчета доходности этого не учитывает и завышает доходность, что не совсем правильно.
Источник
Как рассчитать рентабельность проекта: формула и примеры
Название показателя
Правильное название показателя — Accounting Rate of Return (ARR), в переводе на русский язык — учетная норма прибыли.
Параллельно используется множество синонимов:
- рентабельность проекта;
- коэффициент эффективности инвестиций;
- средневзвешенная ставка рентабельности;
- учетная доходность;
- средняя норма прибыли и другие.
Несмотря на обилие названий, сущность показателя остается неизменной: он определяет, сколько рублей может получить вкладчик за каждый рубль, инвестированный в конкретный проект.
Формула расчета
Есть три варианта расчета учетной нормы прибыли.
Вариант 1. Расчет по средней стоимости вложений
Применяется, если по ходу осуществления проекта все инвестиции будут списаны на расходы без остатка.
ARR = (чистая среднегодовая прибыль / ½ * общая сумма инвестиций) * 100%
Например. Предприятие планирует купить новое оборудование за 3 000 000 рублей. Срок его эксплуатации составляет три года. Ожидаемые расходы составят 1 500 000 рублей в первый год, а дальше будут возрастать на 4% ежегодно. Амортизация будет начисляться линейным способом, то есть каждый год на расходы будет списываться по 1 000 000 рублей. Налог на прибыль — 20%. Прогнозируемая сумма выручки по годам представлена в таблице.
Исходные данные для расчетов:
Таким образом, среднегодовая чистая прибыль = (400 000 + 512 000 + 307 000) / 3 = 406 000 рублей.
ARR = (406 000 / ½ * 3 000 000) * 100% = 27%
Вариант 2. Расчет с учетом остаточной стоимости имущества
Применяется, если нужно учесть остаточную стоимость актива. То есть разницу между его первоначальной стоимостью и суммой износа, начисленной за весь срок его использования.
ARR = (чистая среднегодовая прибыль / ½ * (первоначальные инвестиции — остаточная стоимость)) * 100%
Например. Предприниматель планирует купить производственную линию за 5 200 000 рублей. Износ будет начисляться линейным способом на протяжении пяти лет, то есть каждый год на расходы будет списываться по 1 000 000 рублей. Остаточная стоимость оборудования по истечении срока его эксплуатации составит 200 000 рублей. Прогнозируемая среднегодовая прибыль — 400 000 рублей.
ARR = (400 000 / ½ * (5 200 000 — 200 000)) * 100% = 16%
Вариант 3. Расчет по размеру первоначальных инвестиций
Применяется для оценки проектов, которые обеспечивают равномерный объем доходов на очень длительный или неопределенный срок. К таким проектам относится, например, покупка недвижимости, которую можно сдавать в аренду в течение многих лет.
ARR = (чистая среднегодовая прибыль / сумма инвестиций) * 100%
Например, компания планирует купить недвижимость и сдавать ее в аренду коммерческим предприятиям. Стоимость объекта нежилого фонда — 100 миллионов рублей. Ожидаемая среднегодовая сумма прибыли — 30 миллионов рублей. Подсчитаем рентабельность проекта.
ARR = 30 / 100 * 100% = 30%
Значение показателя в бизнес-планировании
Итак, рентабельность проекта отражает прибыльность объекта инвестирования. Чем она выше, тем больше прибыли получит вкладчик.
Величина показателя сравнивается:
- во-первых, с показателем рентабельности собственного капитала самого предприятия: учетная норма прибыли проекта должна быть выше;
- во-вторых, со среднеотраслевыми значениями рентабельности капитала (показателями конкурентов).
Например, рентабельность собственного капитала компании составляет 30%. То есть на 1 рубль, вложенный в свой бизнес, предприятие получает 30 копеек чистой прибыли. Руководству предложили поучаствовать в новом проекте, норма прибыли которого оценивается в 20%. Стоит ли компании принять предложение? Если других выгод вроде выхода на новые рынки или улучшения деловой репутации сделка не принесет, то не стоит. Ведь доходов от этого проекта будет меньше, чем может получить фирма от своей обычной деятельности.
Универсального значения учетной нормы прибыли не существует. Она зависит от отрасли, в которой планируется реализовать проект. Например, для сельского хозяйства норма прибыли в 15% — очень хороший показатель, он выше среднеотраслевой рентабельности капитала. А для строительства и 50% будет недостаточно.
Величина показателя должна соответствовать степени риска. Если инвестируется стабильное предприятие, давно и плотно занявшее свою нишу на рынке, норма прибыли на уровне среднеотраслевых значений считается хорошей. Но если вкладчику предстоит инвестировать новый инновационный проект, когда существует риск потери дохода или всех вложенных денег, норма рентабельности должна быть на порядок выше.
Если вкладчик выбирает самый доходный проект из нескольких, нужно рассчитать и сравнить нормы прибыли по каждому из них.
Преимущества и недостатки
Основное достоинство учетной нормы прибыли — простота расчета. С другой стороны, она не учитывает такие факторы:
Стоимость денег во времени
В данном случае деньги, поступающие на n-ый год реализации проекта, оцениваются по тому же уровню рентабельности, что и поступления в первый год. Один рубль сегодня стоит больше, чем через год. Деньги можно пустить в оборот и на конец года получить реальный доход. Если же инвестор сможет вернуть вложения только через несколько лет (проект с длительным сроком реализации), то он потеряет возможность получения такого дохода. Кроме того, деньги ежегодно дешевеют из-за инфляции.
Распределение прибыли по годам
Например, инвестор рассматривает два взаимоисключающих проекта. Базовые данные в обоих случаях идентичны: стоимость 20 миллионов рублей, ожидаемая среднегодовая прибыль — 6 миллионов рублей. На первый взгляд проекты выглядят равнозначными, поскольку учетная норма прибыли одинакова:
ARR = (6 / ½ * 20) * 100% = 60%
Однако прогнозируемые объемы прибыли по годам заметно отличаются. В таблице приведены ожидаемые показатели за пять лет реализации проекта.
Из таблицы видно, что второй проект привлекательней для инвестора, поскольку прибыль в первые два года здесь значительно выше.
Разницу в продолжительности срока жизни активов
Если оценивать несколько проектов равной стоимости с приблизительно равной суммой ежегодной прибыли, но разным сроком эксплуатации актива, то результат расчетов будет очень схож. Однако если срок службы активов заметно отличается, то инвестору выгоднее вложить деньги в тот проект, который просуществует дольше.
Сложность прогнозирования будущей прибыли
Если речь идет о новом бизнесе, то прогнозирование прибыли может вызывать затруднения. А в условиях отечественной экономики разброс между ожидаемым и реальным результатом может быть значительным.
Использование различных методов амортизации
Например, амортизация на предприятии начисляется не линейным, а иным способом, то есть сумма варьируется из года в год и спрогнозировать ее нереально. В таком случае расчет по приведенному алгоритму теряет смысл.
Вывод: учетная норма прибыли — удобный и простой инструмент, но область его применения ограничена. Он хорошо подходит для прогнозирования прибыли от внедрения краткосрочных проектов при условии равномерного поступления доходов.
Источник



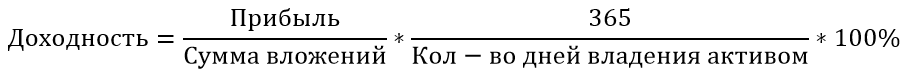
 Как считать среднегодовую доходность
Как считать среднегодовую доходность