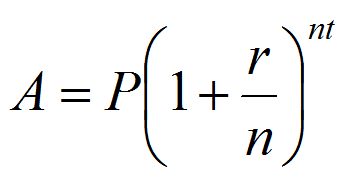Расчет сложного процента для инвестиций

Сложный процент

Сложный процент часто используется в сфере инвестиций. Но посчитать выгоду не так-то просто. Калькулятор сложных процентов на Financer сделает это за вас за 10 секунд.

Сложный процент от А до Я

Это малопонятный термин для тех, кто не работает в инвестиционной или банковской сферах. Однако он нередко фигурирует при оформлении кредита или вклада. Поэтому от грамотных расчетов напрямую зависит ваша прибыль или убытки.

Что такое сложный процент

Если простой каждый отчетный период начисляется на изначальную сумму вклада или займа, сложный постоянно пересчитывается. Например, если отчетный период в организации – 1 год. Это значит, что каждый год к изначальной сумме будет добавляться сумма, полученная с учетом процентной ставки, а на второй год проценты будут высчитывать уже от изначального объема средств + процента за первый год.

Звучит запутанно? Тогда давайте разберемся на живых примерах.

Формула сложных процентов

Расчет сложных процентов производится по формуле A = P (1 + r/n) (nt) , где:

• А – итоговая сумма, которую вы получите на счету (если речь идет о вкладе) или которую вам нужно будет погасить (если речь идет о кредите)
• Р – изначальная сумма вклада или займа
• r – годовая процентная ставка
• n – сколько раз в год учитывается процентная ставка (некоторые учреждения учитывают ее ежемесячно, некоторые – ежеквартально, некоторые – ежегодно, об этом обязательно написано в договоре и в тарифном плане)
• t – число лет, на которые оформлен вклад или кредит

Если вы хотите посчитать только прибыль/переплату по вкладу/кредиту, воспользуйтесь вот такой формулой: P (1 +r/n) ( nt) – P.

Пример расчета сложных процентов для кредита

Допустим, вы взяли потребительский кредит на 1000 рублей под 10% годовых на 5 лет. Причем перерасчет происходит каждые полгода.

Таким образом у нас:

Итого, за 5 лет вы выплатите 1000 * (1 + 0,1/2) (2*5) = 1628

Переплата составит 1000 * (1 + 0,1/2) (2*5) – 1000 = 628

Для сравнения, если бы речь шла о простом проценте, вы бы выплатили за 10 лет 1500 рублей и переплата была бы всего 500.

Пример сложного процента для вклада

Аналогично, допустим вы вложили 1000 рублей под 5% годовых на 2 года. И, допустим, перерасчет идет каждый месяц.

Итого, через 2 года у вас на счету будет 1000*(1 + 0,05/12) (12*2) = 1105

Прибыль составит 1000*(1 + 0,05/12) (12*2) – 1000 = 105 рублей

А если бы речь шла о простом проценте, вы бы получили только 50 рублей прибыли.

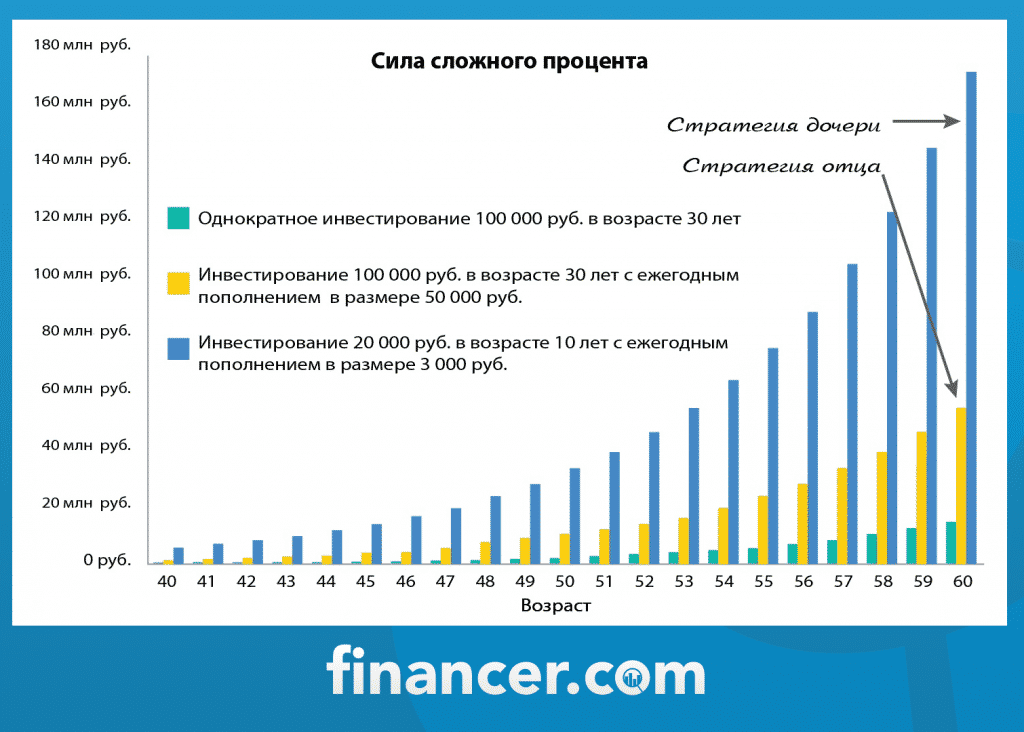
Для сравнения посмотрите на график, наглядно отображающий разницу.

Калькулятор сложных процентов

Как вы видите, самостоятельные расчеты, даже с использованием формулы, не так уж просты. А разница получается существенной. Причем для инвестиций сложный процент получается более выгодным, чем простой, а для кредитов – наоборот.

Но, конечно, вам не нужно углубляться во все эти цифры и что-то считать самостоятельно – вы можете просто воспользоваться нашим калькулятором, который произведет все расчеты онлайн буквально за пару секунд.

А если вас интересуют выгодные предложения по кредитам, воспользуйтесь нашим онлайн сравнением. Так вы сможете выбрать оптимальный вариант за 1 минуту и сразу подать заявку.

Консультант-эксперт с 8-летним опытом работы в области кредитования, финансов, бизнеса и инвестиций. За 2021 год провел анализ более 800 предложений банковских и страховых учреждений.

Управляется Financer.com LTD
VAT MT20908917
financer.com © 2021

FINANCER.COM В МИРЕ

Россия Все филиалы

Войти

Или войдите через email

Неправильное имя пользователя или пароль

Зарегистрироваться

Или зарегистрируйтесь с помощью email

Забыли пароль?

Извините, код введен неправильно или его срок действия истек. Попробуйте еще раз.

Пожалуйста, введите имя пользователя или email. Вы получите письмо на email с инструкциями по изменению пароля.

Введите пароль

Подсказка: Рекомендуется задать пароль длиной не менее двенадцати символов. Чтобы сделать его надёжнее, используйте буквы верхнего и нижнего регистра, числа и символы наподобие ! » ? $ % ^ & ).

Филиалы FInancer.com

Наш сервис работает в 26 странах

Америка (3)

Азия (4)

Европа (19)

Мы используем файлы cookies, чтобы предоставлять наиболее актуальную для вас информацию.

Узнать подробнее об использовании cookies на нашем сайте и/или отключить их вы можете в разделе Настройки.

Необходимые cookie файлы

Этот сайт использует cookies в числе других трекинговых инструментов. Информация из файлов cookies хранится в вашем браузере. Благодаря ей наш узнает вас, когда вы снова заходите на Financer, а мы можем понять, какие страницы и темы для вас наиболее интересны и полезны. Файлы cookies также используются для других маркетинговых и рекламных целей, а также для важной бизнес-аналитики и операций. Чтобы пользоваться нашим сайтом, вам нужно принять Условия Пользования и Политику Конфиденциальности. Чтобы узнать подробности, пожалуйста, прочитайте Условия Использования здесь. Чтобы узнать подробнее о политике конфиденциальности нашего сайта и получить более развернутое описание использования файлов cookies, а также узнать, как вы можете отключить их, пожалуйста, прочтите Политику Конфиденциальности.

Мы используем файлы cookie, чтобы оптимизировать использование сайта на основе ваших предпочтений. За этот функционал отвечают базовые файлы cookie.

В этих файлах сохраняются такие действия как создание и использование аккаунта на нашем сайте, публикация отзывов, лайков, ответов на отзывы и комментарии, настройки слайдера, поиск информации по сайту, индивидуальная настройка пользовательских предпочтений и иные действия, так или иначе связанные с использованием сайта и способные упростить его. Эти файлы cookie позволяют оптимизировать пользовательский опыт, поэтому их можно удалить только вручную с помощью инструкции, указанной в Политике Конфиденциальности.

Мы также используем так называемые «дополнительные файлы cookie», которые позволяют оптимизировать маркетинговую и рекламную политику сайта, а также обеспечить оптимальное использование сервиса для наших пользователей. Они позволяют отслеживать действия пользователя на сайте и связывать их с анонимизированной информацией, предоставляемой сторонними сервисами, такими как Google Ads, Google Analytics, DoubleClick, Bing Ads, Gleam, Typeform, RedTrack, Google Tag Manager, Yahoo, Facebook, YouTube и т.д.

Чтобы узнать подробнее об использовании подобных данных, пожалуйста, ознакомьтесь с нашей Политикой Конфиденциальности, раздел II. Как мы используем информацию о посетителях

Чтобы узнать подробнее о политике конфиденциальности нашего сайта, использовании файлов cookie и возможностях по их отключению, пожалуйста прочитайте статью о Политике Конфиденциальности

Источник

Что такое сложный процент и как инвестору на нём заработать

Команда мобильного приложения «БКС Премьер» рассказывает о том, как увеличить доход от инвестиций с помощью сложного процента.

Оценивая доходность вложений, большинство из нас смотрит на ставку годовых. Но опытные инвесторы знают секрет: важен не только размер, но и метод начисления процентов. Даже небольшая сумма может стать колоссальной, если задействовать всю силу сложного процента.

Это процент, который начисляется на начальную сумму вложений и на проценты, накопленные за предыдущие периоды. Чтобы применить сложный процент, достаточно реинвестировать доход. Вот как это работает на примере банковского вклада.

Предположим, вы положили в банк 50 000 рублей под 10% годовых. Через год ваш доход составит 5 000 рублей. Если вы закроете вклад и снова откроете его на тех же условиях, прибавив к основной сумме заработанные 5 000 рублей, в следующем году ваш доход составит 10% от 55 000 рублей, то есть 5 500 рублей. Ещё через год доход вырастет до 6 050 рублей. Это и есть сложный процент, в банковских вкладах его называют капитализацией.

Благодаря сложному проценту накопления растут как снежный ком: ваши инвестиции приносят доход, а затем этот доход приносит новый доход и так далее.

Сравним, как будет расти вклад при начислении простого и сложного процента в течение нескольких лет.

Из примера очевидно, что сложный процент приносит максимальный эффект на длинной дистанции. Чем раньше вы начнете инвестировать, тем больше сможете заработать к намеченной дате.

Рассчитать сложный процент можно по формуле:

Sₙ = (1 + P/100)ᴺ х S

где Sₙ — размер вашего капитала в конце срока инвестирования, Р — процентная ставка, S — начальная сумма вложений, а N — количество периодов реинвестирования.

Чтобы не считать вручную, воспользуйтесь калькулятором сложного процента. Просто скопируйте таблицу на свой гугл-диск и укажите свои условия инвестирования.Как сложный процент работает в инвестициях

Эффект сложного процента применим не только к банковским вкладам, но и к другим инвестиционным инструментам. Рассмотрим, как его использовать при вложениях в облигации и акции.

Владельцы облигаций получают процент от вложений — купонный доход. Он выплачивается раз в квартал, полгода или год. Инвестируя в облигации с фиксированным купоном, вы можете спрогнозировать денежный поток и заранее подумать о том, как его использовать. Если вы не планируете жить на купонный доход, лучшее решение — вложить его в покупку той же или похожей облигации. Это позволит существенно увеличить заработок в долгосрочной перспективе.

Реинвестировать купонный доход получится только в том случае, если его хватает на покупку дополнительных ценных бумаг. Если вы купили одну ОФЗ-ПД 26227 и получили по ней купон в размере 36,9 рублей, приобрести ещё одну такую же облигацию федерального займа не удастся — на данный момент бумага стоит 1070 рублей. Но совсем другое дело, если у вас 50 шт. ОФЗ-ПД 26227. Годовая купонная выплата по ним составит 3 690 рублей. На эти деньги можно купить ещё 3 таких же ОФЗ и увеличить следующий купонный доход. Схему можно повторять сколько угодно, получая от сложного процента максимум выгоды.

Доходность облигаций с учетом реинвестирования купонов называется эффективной доходностью. Считать её вручную необязательно — гораздо проще воспользоваться облигационным калькулятором на сайте Мосбиржи. Например, эффективная доходность ОФЗ-ПД 26227 на данный момент составляет 7,54%.

Покупать облигации и реинвестировать купонный доход ещё выгоднее на ИИС — так вы можете не только повысить доходность вложений, но и получить налоговый вычет в размере 13% от внесенной на счет суммы. Открыть ИИС можно в приложении БКС Премьер. Это быстро, бесплатно и полностью онлайн.

Аналогичным образом сложный процент работает и при инвестировании в дивидендные акции. Допустим, вы вложили 1000 рублей в акции со стабильной годовой доходностью 10%. В случае с простым процентом ваша доходность всегда будет 10% — вы удвоите свой капитал за 10 лет. Если же вы будете реинвестировать полученные дивиденды в те же акции, в будущем получите ещё больше дивидендов, а удвоить капитал удастся примерно за 7 лет. Но обратите внимание: приведенный пример достаточно условен, в реальности доходность акций будет меняться в зависимости от экономической ситуации и финансовых результатов компании.

Многие инвесторы предпочитают держать капитал в акциях с умеренной, но стабильной дивидендной доходностью, а на полученные дивиденды покупать ценные бумаги с высоким потенциалом роста. Такая схема позволяет достичь баланса между защитой капитала и возможностью увеличить доход за счет высокорисковых инструментов.

Применять сложный процент можно не только при получении дивидендов. Если вы зарабатываете на росте стоимости акций — покупаете дешевле, а продаете дороже, — вы также можете реинвестировать прибыль в покупку новых ценных бумаг, увеличивая тем самым доходность вложений. Но в этом случае результат инвестирования сложно предсказать — он будет зависеть от того, насколько выгодно вы продаете и покупаете акции и в какие бумаги реинвестируете прибыль.

Чтобы зарабатывать на инвестициях больше, задействуйте механизм сложного процента. Для этого достаточно реинвестировать полученный доход в те же или другие финансовые инструменты. Например, вы можете потратить купонный доход на покупку дополнительных облигаций или вложить полученные дивиденды в новые акции того же эмитента. Такой подход позволит значительно увеличить капитал в долгосрочной перспективе и гораздо быстрее достичь финансовых целей.

Эта статья не является инвестиционной рекомендацией.

Источник

Сложные проценты с ежемесячным внесением платежа

Расчет наращенной суммы при ежемесячном внесении платежа.

Выполняем просьбу пользователя frouzen, который просил написать Финансовый калькулятор. — рассчитывающий наращенную сумму при использовании сложных процентов и довложении средств ежемесячно равными платежами. Начисление процентов предполагается тоже ежемесячное (самый выгодный случай).

Чтобы не отвлекать пользователя от калькулятора, ниже идет сам калькулятор, а немного теории и формул надо смотреть под ним, кому не лень.

Сложные проценты с ежемесячным вложением равной суммы

Формула сложных процентов, начисляемых несколько раз в течении года
, где m в нашем случае равно 12, а n — срок вклада в годах

Это простейший случай при внесении вклада сразу, и без дальнейшего его пополнения.

Теперь займемся более сложным случаем — пополнением вклада одинаковыми платежами ежемесячно.
Заметим, что множитель степени mn не что иное, как число периодов начисления процентов.

Таким образом, для самого первого вклада за несколько лет наращенная сумма будет равна

Для вклада, который был внесен в конце первого месяца, число периодов начисления процентов на один меньше, и формула будет выглядеть так
,
для третьего вклада — так
,
.
и для последнего вклада, то есть внесенного за месяц до окончания срока — так
,

Интересующий нас результат равен сумме всех этих выражений. И эти выражения кое-что роднит — все они члены геометрической прогрессии, в которой первый член равен , а знаменатель прогрессии равен .

Про геометрическую прогрессию смотри Геометрическая прогрессия

Таким образом, искомая сумма по формуле суммы геометрической прогрессии равна

Вот и все на сегодня.

Обновление

По просьбе пользователя добавлена возможность отдельного указания размера первого взноса.

Источник