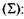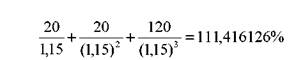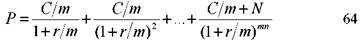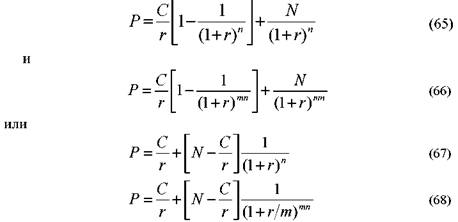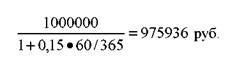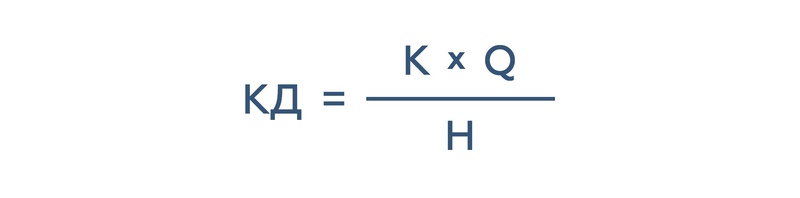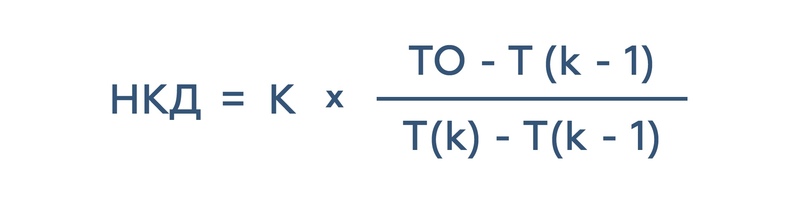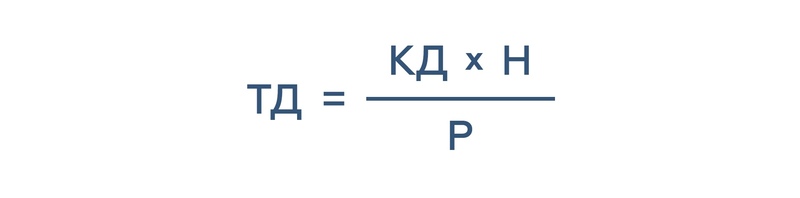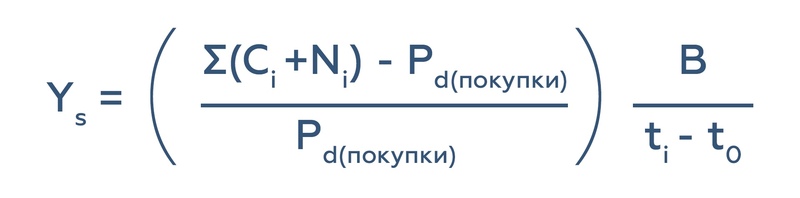Определение курсовой стоимости и доходности облигаций
Определение курсовой стоимости и доходности ценных бумаг
В настоящей главе рассматривается техника расчетов курсовой стоимости и доходности ценных бумаг. Вначале мы остановимся на определении курсовой стоимости и доходности облигаций. После этого перейдем к акциям, векселям и банковским сертификатам.
Определение курсовой стоимости облигаций.
Определение курсовой стоимости ценных бумаг основано на принципе дисконтирования, рассмотренного нами в главе 3. Инвестор приобретает ценную бумагу, чтобы получать доходы, которые она приносит. Поэтому для ответа на вопрос, сколько сегодня должна стоить та или иная ценная бумага, необходимо определить дисконтированную стоимость всех доходов, которые она принесет.
Технику определения курсовой стоимости можно представить в три действия. 1) Определяем поток доходов, который ожидается по ценной бумаге. 2) Находим дисконтированную (сегодняшнюю) стоимость величины каждого платежа по бумаге. 3) Суммируем дисконтированные стоимости. Данная сумма и представляет собой курсовую стоимость ценной бумаги.
После того как мы привели общий принцип расчета курсовой стоимости, рассмотрим определение курса различных видов облигаций.
Определение курсовой стоимости купонной облигации
Рассмотрим пример. Номинал облигации равен 1 млн. руб., купон — 20%, выплачивается один раз в год, до погашения остается три года. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в 25%. Определить курсовую стоимость бумаги.
Определяем поток доходов, который принесет облигация инвестору за три года. В конце каждого года инвестор получит купон в сумме 200 тыс. руб., и в конце третьего года ему выплатят сумму номинала в размере 1 млн. руб. Таким образом, облигация принесет следующий поток доходов.
Определяем дисконтированную стоимость суммы каждого платежа по облигации. Для первого платежа она равна:
где: Р — цена облигации,
п — число лет до погашения облигации;
r — доходность до погашения облигации. 1
В формуле (62) важно отметить, что п — это количество лет, которые остаются до погашения бумаги. Например, облигация выпущена на 10 лет, однако 7 лет уже прошло. Определяя курсовую стоимость такой бумаги следует взять п равной трем. Это вытекает из принципа дисконтирования будущих доходов. В данном случае облигация принесет доходы инвестору только за три оставшиеся года.
В формуле (62) появилось такое понятие как доходность до погашения (или доходность к погашению). Доходность до погашения — это доходность в расчете на год, которую обеспечит себе инвестор, если, купив облигацию, продержит ее до погашения. В нашем примере, заплатив за облигацию 902400 руб., вкладчик обеспечил себе ежегодную доходность из расчета 25% годовых. Если владелец облигации продаст ее до момента погашения, то, как правило, он не получит данного уровня доходности, так как конечный результат его операции будет зависеть от цены продажи облигации на рынке.
при расчете цены облигации является определение ставки дисконтирования. Она должна соответствовать уровню риска инвестиций. В нашем примере данная ставка составляла 25%. На практике ее можно взять, например, из котировок, брокерских компаний по облигациям с похожими характеристиками. Ее также можно попытаться определить аналитически, разложив ставку на составные части. Ставку дисконтирования можно представить следующим образом:
,
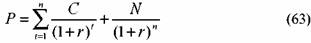
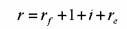
rf — ставка без риска, т. е. ставка по инвестициям, для которых отсутствует риск; в качестве такой ставки берут доходность по государственным ценным бумагам для соответствующих сроков погашения,
l — премия за ликвидность,
i— темп инфляции,
re — реальная ставка процента.
риска (rf) может учитывать инфляцию. Однако если инвестор полагает, что инфляция будет развиваться более высоким темпом, он также учтет это в ставке дисконтирования. Приобретая бумагу, инвестор сталкивается с риском ликвидности, который связан с тем, насколько быстро и по какой цене можно продать бумагу.
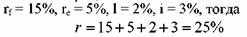
Поэтому данная величина должна найти отражение в ставке дисконтирования.
Ставку дисконтирования также можно определить аналитически, о чем будет сказано в главе, посвященной управлению портфелем ценных бумаг.
Рассмотрим еще один пример. N = 1млн. руб., купон — 20%, доходность до погашения — 15%, до погашения остается три года.
Цена облигации равна:
случае цена облигации оказалась выше номинала. Такая ситуация объясняется тем, что, согласно условиям примера, рынок требует по облигации доходность до погашения на уровне 15% годовых. Однако по ней выплачивается более высокий купон — 20%. Каким образом инвестор может получить более низкую доходность, чем 20%? Это возможно лишь в том случае, если он приобретет облигацию по цене выше номинала. При погашении облигации ему выплатят только номинал. Поэтому сумма премии, которую он уплатил сверх номинала, уменьшит доходность его операции до 15%.
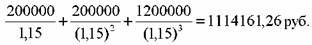
Между курсовой стоимостью и доходностью до погашения облигации существуют следующие зависимости.
Цена облигации и доходность до погашения находятся в обратной связи. При повышении доходности цена облигации падает, при понижении — возрастает.
Если доходность до погашения выше купонного процента, облигация продается со скидкой.
Если доходность до погашения ниже купонного процента, облигация продается с премией.
Если доходность до погашения равна купонному проценту, цена облигации равна номиналу.
При понижении доходности до погашения на 1° о цена облигации возрастает в большей степени в сравнении с ее падением при увеличении доходности до погашения на 1%.
Как уже отмечалось, котировки облигаций приводятся в процентах к номинальной стоимости. Поэтому при определении курсовой стоимости облигации можно пользоваться не величинами в денежном выражении, а в процентах. В этом случае номинал принимается за 100%. В качестве иллюстрации запишем приведенный выше пример с использованием процентов:
Купон по облигации может выплачиваться чаще, чем один раз в год. В таком случае формула (63) примет вид:
где: т — частота выплаты купона в течение года.
Как видно из формулы (64), количество слагаемых увеличивается в т раз. Дополним наш последний пример условием, что купон выплачивается два раза в год, и найдем цену облигации:
Формулы (63) и (64) можно привести к более удобному виду, учитывая тот факт, что выплата купонов представляет собой не что иное как аннуитет:
Приведенные формулы позволяют рассчитать чистую цену облигации, т. е. цену на основе целых купонных периодов. Однако бумаги продаются и покупаются также в ходе купонного периода. Поэтому следует ответить на вопрос, каким образом рассчитать полную цену облигации, т. е. цену, скорректированную на размер накопленных к моменту сделки суммы купонных процентов. Общий подход и в данном случае остается прежним, т. е. необходимо дисконтировать будущие доходы с учетом времени, которое остается до их получения.
N = 100 тыс. руб., r = 20%, купон равен 10% и выплачивается один раз в год. До погашения облигации остается 2 года 345 дней. Определить цену облигации.
примере первый купон инвестор получит через 345 дней, второй — через год 345 дней и третий купон вместе с номинальной стоимостью — через два года 345 дней. В общем виде формула определения цены облигации для такого случая, когда купон выплачивается один раз в год, имеет следующий вид:
число дней с момента сделки до выплаты очередного купона;
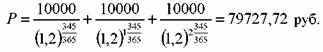
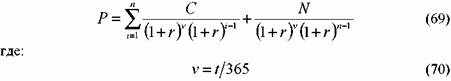
п — целое число лет, которое остается до погашения облигации, включая текущий год.
Если купон выплачивается т раз в год, то число купонных периодов в формуле (69) корректируется на т, как было показано выше, а в знаменателе формулы (69) вместо 365 дней указывается число дней в купонном периоде.
1. 1. 2. Определение курсовой стоимости среднесрочной и долгосрочной бескупонных облигаций.
Формулу определения курсовой стоимости бескупонной облигации можно получить из формулы (69). Поскольку по облигации не выплачиваются купоны, то С = 0 и формула (69) принимает вид:
N = 10000 руб., r = 20%, п = 3 года. Определить Р.
облигации остается не целое число лет, то формула (71) примет вид:
— число дней от момента сделки до начала целого годового периода для облигации;
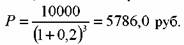
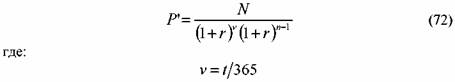
п — целое число лет, которое остается до погашения облигации, включая текущий год.
На практике приходится сравнивать купонные и бескупонные облигации. В этом случае необходимо помнить о следующем правиле. Если по купонным облигациям процент выплачивается т раз в год, то формулу (71) следует также скорректировать на т, а именно:
начисления сложного процента во всех финансовых расчетах.
5. 1. 1. 3. Определение курсовой стоимости ГКО Цена ГКО определяется по формуле:
N— номинал ГКО; r — доходность до погашения; t — количество дней от момента сделки до погашения ГКО.
N = 1 млн. руб., t = 60 дней, r = 15%. Определить цену ГКО. Она равна:
5. 1. 1. 4. Определение курсовой стоимости ОФЗПК и ОГСЗ
Цена данных облигаций определяется стандартным способом, т. е. будущие доходы по облигациям дисконтируются к сегодняшнему дню и суммируются. Особенностью ОФЗ-ПК и ОГСЗ является то, что купоны у них плавающие и их величина изменяется в зависимости от ситуации на рынке ГКО. Поэтому инвестору необходимо вначале сделать прогноз относительно ситуации на рынке ГКО. Затем оценить величину будущих купонов и дисконтировать их и номинал к сегодняшнему дню.
Мы рассмотрели формулы определения курсовой стоимости облигаций. Они позволяют инвестору рассчитать приемлемый для него уровень цены бумаги. В то же время это не означает, что облигации на рынке обязательно будут продаваться по найденной цене. Так происходит потому, что различные вкладчики поразному могут оценивать риск приобретения облигации, и, следовательно, использовать несколько отличные ставки дисконтирования. Кроме того, на цену будут также влиять силы спроса и предложения. Если спрос превышает предложение, то это создаст потенциал к повышению цены, если предложение больше спроса, то — то к понижению.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Купонная доходность и накопленный купонный доход
При покупке облигаций нас больше всего интересует, какую доходность мы получим. Выделяют разные доходности: текущая доходность, купонная доходность и доходность к погашению.
Купонная доходность определяется в процентах годовых, зависит от процентных ставок и конъюнктуры рынка в целом.
Если купон выплачивается несколько раз, применяем развернутую формулу:
Где :
К — размер купона
Q — количество купонных периодов за календарный год
Н — номинал облигации
Например, ОФЗ 26209:
Выплаты производятся 2 раза в год, купон в абсолютном выражении — 37,90р., номинал −1000р.
Рассчитываем купонную доходность:
КД=(37,9*2)/(1000)*100%=7,6%.
Купонная доходность выражается в процентах годовых. Используя эту же формулу, мы можем рассчитать годовой доход в абсолютном выражении.
При расчете стоимости облигации, следует обратить внимание на накопленный купонный доход (НКД). Как мы говорили ранее, НКД — это часть купона, рассчитываемая пропорционально количеству дней, между датами выплаты купона.
Приведем формулу НКД:
Где:
К — размер текущего купона (в денежных единицах)
Т0 — текущая дата
Т(к-1) — дата начала купонного периода
Т(к) — дата выплаты ближайшего купона
Пример по ОФЗ 26205:
На 04.05.2017г. НКД составляет 3,33р. Низкая сумма свидетельствует о недавней выплате купона. Смотрим информацию о предыдущей выплате — она состоялась 19.04.2017г. Текущая цена данной облигации — 99,87%, это свидетельствует, что данная бумага торгуется ниже номинала и стоимость одной облигации составляет 998,7р. Кроме этого, нам необходимо заплатить НКД в размере 3,33р., и комиссию брокера. Тем самым, мы компенсируем предыдущему держателю упущенную выгоду.
Если мы захотим продать облигацию до срока выплаты купона, то новый держатель должен будет заплатить нам сумму НКД на дату продажи, компенсировав прибыль купона. НКД подобен капитализации процентов по банковскому вкладу.
Из приведенного примера видно, что облигации можно купить по цене ниже или выше номинала. Рассмотрим пример расчета НКД.
Вернемся к ОФЗ 26209:
Сумма купона равна 37,9р. Текущая дата 05.05.2017, дата выплаты последнего купона — 25.01.2017. Дата ближайшего выплаты купона — 26.07.2017. Подставляем данные в формулу, получаем:
НКД=37,9*(05.05.2017-25.01.2017)/(26.07.2017-25.01.2017)=20,824 р.
Облигация, которая торгуется выше цены номинала, торгуется с премией — ажио, а ниже номинала — с дисконтом — дизажио.
Купонная доходность актуальна только в случае покупки облигации по номинальной стоимости и удержанию до погашения (или — продажи до срока погашения по оферте или по номинальной стоимости на вторичном рынке). В случае покупки облигации на вторичном рынке по цене, отличной от номинала (с дисконтом или премией), более важным показателем является текущая доходность.
Текущая доходность и доходность к погашению
Текущая доходность (ТД) для облигации с фиксированным купоном определяется как отношение годовой купонной доходности облигации к цене приобретения.
Приведем формулу ТД:
Где:
КД — купонная доходность
Р — рыночная цена облигации (цена приобретения)
Н — номинал облигации
На примере с ОФЗ 26209:
Купонный доход равен 7,6%, номинал — 1000р., рыночная цена — 99,7%, т.е. 997р. Подставляем данные в формулу, получаем:
ТД=(7,6%*1000/99,7%*1000)*100%=7,62%.
Из формулы очевидно, что текущая доходность облигаций, приобретенных с дисконтом, будет выше купонной доходности, а ТД облигаций, приобретенных с премией — ниже КД. В случае, если облигация приобреталась по номинальной стоимости, купонная доходность равна текущей.
Доходность к погашению — наиболее универсальный инструмент для оценки различных вариантов инвестирования в облигации.
Где:
Ys — простая доходность к погашению, % годовых
Ci — величина i-го купонного платежа, руб.
Ni — величина i-ой выплаты номинала (включая выкуп основной скммы долга по оферте, выплаты по амортизации, погашение), руб.
Pd — грязная цена облигации (т.е. номинал + НКД), руб.
ti — дата i-ой выплаты купона, номинала и пр.
to — текущая дата или дата, на которую производится расчет
B — база расчета, число дней в году (обычно 365)
Владелец облигации может реинвестировать полученные купоны в ту же облигацию, или в облигацию с аналогичными рыночными характеристиками, и благодаря этому получить больший доход, нежели без реинвестирования.
Факторы, влияющие на стоимость и доходность облигаций
Определим факторы, влияющие на формирование стоимости облигаций:
- Кредитный рейтинг эмитента (если рейтинг низкий, то риск повышается, и доходность растет)
- Срок обращения (чем больше срок обращения, тем больше должен быть процент, однако и волатильность данных бумаг выше)
- Финансовое положение компании (в случае, если речь идет о корпоративных облигациях. Этому посвящен фундаментальный анализ предприятия)
- Уровень налогообложения
- Новостной фон
Как мы говорили ранее, размер купона зависит от срока обращения облигации и конъюнктуры рынка.
Крупная компания может выпускать облигации на более длительный срок, чем компания малого бизнеса. Ставка купона по таким бумагам выше, но, вследствие длительного срока обращения, инвестор должен быть готов вложить денежные средства на длительный срок. Небольшие компании обычно выпускают облигации на малый срок (если бы такая компания решила эмитировать облигации с долгим сроком обращения, возникла бы необходимость увеличения купона, а это экономически нецелесообразно).
Рассмотрим на конкретных примерах изменение купонной доходности облигаций, в зависимости от надежности эмитента и срока погашения:
| Облигация | Дата размещения | Дата погашения | Вид купона | Купонная доходность, % |
|---|---|---|---|---|
| ОФЗ-25081 | 06.02.2013 | 31.01.2018 | пд | 6,2 |
| ОФЗ-26219 | 29.06.2016 | 16.09.2026 | пд | 7,75 |
| ОФЗ-26221 | 15.02.2017 | 23.03.2033 | пд | 7,7 |
| ОФЗ-24019 | 30.11.2016 | 16.10.2019 | пк | 10,5 |
| ОФЗ-29008 | 31.12.2014 | 03.10.2029 | пк | 11,45 |
| Внешэкономбанк-001Р-06-об | 30.03.2017 | 27.07.2018 | пд | 9,45 |
| ОКЕЙ-5-боб | 28.04.2015 | 21.04.2020 | пд | 10,5 |
| ПИК ГК-БО-П01 | 03.03.2017 | 25.02.2022 | пк | 13 |
| Альфа-Банк-13-боб | 18.09.2014 | 30.08.2029 | пк | 9,33 |
Если говорить про ОФЗ, то данные облигации проблематично найти на срок менее 2 лет. Так как объем эмиссии обычно высокий, срок обращения приближен к среднесрочному. Бывают случаи, когда компаниям привлекательно разместить корпоративные облигации на один год, под хороший процент, так как данный процент будет ниже процента по кредиту банка.
Дюрация
Теперь давайте рассмотрим еще одно важное понятие, касающееся стоимости облигаций — это дюрация.
Дюрация — это показатель, определяющий, через какой промежуток времени инвестор получит свои вложения обратно.
Формула расчеты дюрации довольно сложна для инвестора нет необходимости знать ее наизусть. Для лучшего понимания этого показателя давайте обратимся к простому жизненному примеру: вас просят занять денежные средства два человека: Иван и Петр.
И тот, и другой занимают сумму в 100 000 рублей под 15% годовых на срок в 3 года.
Разница в их предложении заключается в том, что Иван готов выплачивать проценты ежемесячно с возвратом долга в конце срока, а Петр может лишь через 3 года вернуть все проценты вместе с самим телом долга. Кому вы займете деньги?
Ответ очевиден: Ивану. Ведь с первого месяца вы уже начнете получать прибыль, а риск частичного или полного невозврата будет становиться ниже.
Дюрация для инвестора является конечным фильтром при выборе облигаций. Когда мы сравниваем две одинаковые по кредитоспособности и дате погашения облигации, мы отдаем предпочтение той, у которой дюрация ниже.
Пример, приведенный выше, описывает смысл дюрации без учета влияния процентных ставок в стране.
Существует обратная зависимость между изменением процентных ставок и стоимостью облигаций. Когда ставка поднимается, рыночная стоимость облигаций снижается. И наоборот — когда в стране действуют высокие процентные ставки, выгоднее брать облигации с длительной дюрацией. Почему?
Например, в этом году процентная ставка в стране 15%, в следующем году она прогнозируется на уровне 10% и далее ожидается ее снижение.
Облигации, выпускающиеся в следующем году, будут так же давать около 10% годовых. При этом облигации этого года будут давать доходность в 1,5 раза выше. Такие выгодные облигации никто не захочет продавать по номиналу, соответственно цена на «старые» выпуски с более высоким процентом автоматически повысится.
Если вы ожидаете, что в дальнейшем процентная ставка будет снижаться, то ее изменение приведет к увеличению стоимости облигации. Чем больше дюрация, тем на большее увеличение стоимости (и дохода) можно рассчитывать.
И так же наоборот: при ожидании повышения процентных ставок в будущем, необходимо обращать внимание на бумаги с наименьшей дюрацией.
Риски, связанные с инвестированием в облигации
Перейдем к рискам, которые следует учесть при инвестировании в облигации. С ними также связано изменение стоимости облигаций:
- Риск, связанный с процентными ставками: цена облигации будет двигаться в направлении, противоположном движению процентных ставок. При падении процентных ставок, цена на облигации будет расти. Это относится в большей степени к облигациям с переменным купоном.
- Риск, связанный с реинвестированием: инвестор рискует реинвестировать промежуточный денежный поток по более низким процентным ставкам. Первый и второй риски способны сбалансировать друг друга.
- Кредитный риск, или риск невыполнения эмитентом взятых на себя обязательств.
- Риск инфляции: изменение стоимости денежного потока.
- Риск, связанный с изменением курса валют.
- Риск ликвидности: невозможность продать облигацию по близкой к её справедливой стоимости.
- Риск волатильности: ожидаемая волатильность процентных ставок.
Основные причины изменения цены облигации:
- Изменение доходности, связанное с изменением кредитного качества эмитента;
- Цена облигации изменяется в зависимости от приближения даты погашения;
- Изменение доходности, связанное с изменением доходности аналогичных облигаций.
Кредитный рейтинг эмитента
Рассмотрим более подробно влияние кредитного рейтинга эмитента на формирование цены облигации. Облигация является инструментом с фиксированной доходностью, поэтому главным риском, который несет ее держатель, является риск неплатежеспособности эмитента облигации. Оценка этого риска — это функциия кредитного рейтинга эмитента облигации, который присваивается каждой публичной компании независимыми рейтинговыми агентствами, крупнейшие из них:
- Fitch, Inc.
- Moody’s Investors Service, Inc.
- Standard & Poor’s Ratings Services.
В России есть собственные рейтинговые агентства — «Эксперт РА», Национальное Рейтинговое Агентство (НРА), АК&M.
Ознакомиться с кредитными рейтингами интересующих вас эмитентов облигаций можно, например, на сайте Cbonds, в разделе «История кредитных рейтингов».
Рейтинговые агентства производят оценку кредитоспособности эмитентов облигаций по единой системе, использующей буквенные обозначения: от А (самый высокий рейтинг) до D (дефолт, банкротство). Границей между инвестиционным и спекулятивным уровнем кредитного рейтинга является уровень ВВВ- (по версии агентств Moody’s и Standard & Poor’s).
Кредитный рейтинг эмитента облигации и ставка купона находятся в обратно пропорциональной зависимости. Облигации инвестиционного уровня надежности являются надежным источником инвестирования на среднесрочную и долгосрочную перспективу, и их доходность, как правило, находится на уровне средней по стране доходности банковских депозитов. При этом риски неплатежеспособности эмитента по этим облигациям минимальны, и вероятность получения заявленного дохода — достаточно высока.
Облигации со спекулятивным рейтингом имеют гораздо более привлекательные купонные ставки, при этом риски неплатежеспособности эмитента пропорционально возрастают, а вероятность фактического получения заявленного купонного дохода — снижается.
Рейтинг не присваивается облигациям, выпущенным центральными государственными органами — они считаются «абсолютно надежными» в рамках данного государства, то есть их рейтинг по умолчанию считается равным рейтингу государства.
Налоговые аспекты рынка облигаций
Конечно, при покупке облигаций инвестор должен учитывать не только рыночную стоимость и доходность облигации, но и налоговую нагрузку, которая также влияет на результаты инвестирования.
В настоящее время всё больше предпочтений отдается рынку облигаций. При этом действия правительства направлены на уравнивание инвестиционной привлекательности банковских депозитов и облигаций. В РФ стандартная налоговая ставка по налогу на доход с покупки/продажи облигаций для физических лиц-резидентов установлена в размере 13% — по ней происходит налогообложение большей части доходов, получаемых частными инвесторами на рынке ценных бумаг.
Купоны по государственным и муниципальным облигациям налогом на доходы физических лиц не облагаются. Если частный инвестор приобретает такие инструменты по цене, превышающей номинальную стоимость или равной ей, и владеет ими вплоть до погашения, то обязанности по уплате налога у него не возникает.
Обычные корпоративные облигации ранее облагались НДФЛ как с купонного дохода, так и курсовой разницы цены покупки и цены продажи.
На заседании 22 марта 2017 года Госдума приняла в третьем чтении законопроект об освобождении физических и юридических лиц от уплаты НДФЛ с купонного дохода по рублевым облигациям, выпущенным в период с 1 января 2017 года по 31 декабря 2020 года. 29 марта этот документ, представляющий собой поправки в 23-ю главу части второй Налогового кодекса, был утвержден Советом Федерации. После подписания президентом он официально вступил в силу. Согласно его положениям частным инвесторам больше не придется платить налог в 13% на купонный доход от облигаций российских компаний. Кроме того, если владелец бумаги планирует держать ее до погашения — он освобождается от уплаты НДФЛ на разницу между ценой покупки и номиналом облигации.
Из-под НДФЛ выведены «доходы в виде купонов, выплаченных по обращающимся облигациям российских организаций, номинированных в рублях», но не в полном объеме, а лишь проценты, не превышающие увеличенную на 5 процентных пунктов ставку рефинансирования ЦБ (которая на сентябрь 2018 года составляет 7,5%). С сумм, начисленных сверх ставки рефинансирования плюс 5%, физические лица будут платить налог.
Таким образом, при действующей ставке рефинансирования, под налог попадут суммы купонных выплат, начисленные сверх 12,5% годовых.
Данными налоговыми льготами можно пользоваться с 2018 года.
Источник