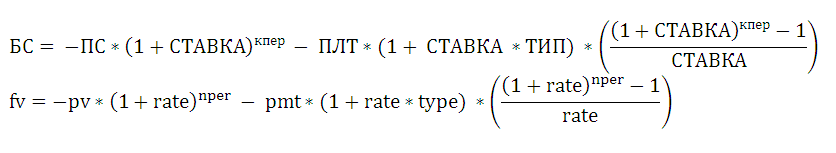Расчет будущей стоимости инвестиций формула

Будущая стоимость инвестиций – это сумма, до которой возрастет первоначальный вклад с учетом капитализации на основе сложных процентов, в течение периода хранения средств на счете.

Расчет будущей стоимости инвестиций осуществляется с использованием стандартных формул.

Чтобы их усвоить, достаточно попрактиковаться на простом примере.

Допустим, у нас имеется вклад в размере 1000 долл. под 7% годовых. Будущая стоимость инвестиций в данном случае может быть рассчитана по следующей формуле:

Будущая стоимость на конец 1-го периода = 1000 долл. * (1 + 0,07) = 1070 долл.

В случае продления срока действия вклада на тех же условиях еще на год будущую стоимость вклада следует рассчитывать по той же формуле с учетом полученного результата:

Будущая стоимость на конец 2-го периода = 1070 долл. * (1 + 0,07) = 1144,9 долл.

Понятно, что этот процесс может быть продолжен сколь угодно долго.

Формула расчета будущей стоимости инвестиций

Было бы удобно, не производя промежуточных расчетов, сразу получать значения будущей стоимости денег (инвестиций) на некоторый период времени, располагая данными о [1] размере первоначального вклада и [2] размере процентной ставки.

Для этого выведем общую формулу.

Для сокращения записи обозначим будущую стоимость инвестиций на конец n-го периода буквой S_n, размер первоначального вклада – буквой N, размер процентной ставки – k.

Тогда наша формула примет вид:

В частности, будущая стоимость инвестиций на конец 2-го периода с учетом наших первоначальных данных будет рассчитана по формуле 1000 долл. * (1+7/100) 2 = 1000 долл. * 1,1449 = 1144,9 долл., что соответствует полученному нами ранее результату.

Таблица расчета будущей стоимости инвестиций

На практике производить вручную приведенные выше расчеты бывает крайне утомительным.

Рассчитать будущую стоимость инвестиций на конец хотя бы 10-го периода способны разве что истинные фанаты счетного дела.

Попробуйте, к примеру, возвести в 10-ю степень число 1,07; лично я сразу начинаю искать калькулятор или что-то в этом роде…

До изобретения калькуляторов и компьютеров широко использовались таблицы с уже готовыми результатами.

На практике такие таблицы могут оказаться очень удобными в использовании.

Чтобы было понятно, о чем идет речь, предлагаю взглянуть на таблицу ниже:

Таблица содержит коэффициенты для 1 долл. (значения коэффициентов округлены до 3-го знака после запятой).

В частности, по истечению 2-го периода (года) при 7-процентной ставке размер вклада составит 1,145 долл. Если первоначальная сумма вклада составляла 1000 долл., то для расчета будущей стоимости вклада нужно его первоначальный размер умножить на соответствующий коэффициент из таблицы (1000 долл. * 1,145 = 1145 долл.).

Будущая стоимость инвестиций: важные закономерности

Внимательно присмотревшись к таблице, можно сделать несколько основополагающих выводов относительно формирования будущей стоимости инвестиций.

Во-первых, чем выше процентная ставка по вкладу, тем выше размер будущей стоимости.

Во-вторых, для каждой процентной ставки характерно увеличение размера будущей стоимости инвестиций с течением времени.

Наконец, в-третьих, коэффициент наращения будущей стоимости, как правило, всегда больше 1; он может быть равен 1 лишь в случае, когда процентная ставка равна 0.

В таком случае будущая стоимость инвестиций оказывается равной первоначальному вкладу, что случается, например, когда, вы просто одалживаете деньги на некоторый срок своим знакомым без взимания процентов за пользование одолженными средствами.

Конечно, использование таблиц не лишено недостатков.

Их расширение может представлять определенные трудности.

Если нам понадобится узнать размер капитала через 100 периодов, потребуется довольно обширная таблица, пользование которой окажется не таким уж простым делом.

На сегодняшний момент оптимальным следует признать использование так называемых инвестиционных калькуляторов, позволяющих в режиме онлайн производить соответствующие расчеты и мгновенно получать интересующие нас результаты.

Резюме

Сегодняшняя статья не охватывает всех аспектов, касающихся описания концепции сложных процентов и концепции будущей стоимости, а также связанных с этими концепциями расчетов.

Существует ряд формул, позволяющих рассчитывать будущую стоимость аннуитета (потока равных сумм денежных средств), приведенной стоимости, которые будет полезно усвоить каждому вдумчивому инвестору.

Но обо всем об этом мы поговорим в другой раз. Так что до скорой встречи и удачных инвестиций!

Источник

Расчет Будущей стоимости в EXCEL

history 3 февраля 2015 г.

Рассчитаем Будущую стоимость инвестиции для различных способов начисления процента: по формуле простых процентов, сложных процентов и формуле аннуитета.

Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и Приведенной (Текущей) стоимости важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту.

Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты: простые проценты , сложные проценты или аннуитет (в файле примера приведено решение задачи для каждого из методов).

Простые проценты

Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты, начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).

При начислении простых процентов формула для расчета будущей стоимости (FV) инвестиций имеет следующий вид:

где PV — настоящая (приведенная) стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц (=годовая ставка/12)); n – количество периодов времени, в течение которых начисляются проценты.

Как видно из формулы FV (в MS EXCEL используется аббревиатура БС) это ни что иное, как наращенная сумма с использованием простых процентов. Про вычисление наращенной суммы при постоянной и переменной ставке можно прочитать в статье Простые проценты в MS EXCEL .

Примечание . В MS EXCEL нет отдельной функции для расчета Будущей стоимости по методу Простых процентов. Функция БС() используется только для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить БС() рассчитать Будущую стоимость и по методу простых процентов (см. файл примера ).

Сложные проценты

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент» (см. файл примера ). Формула для расчета Будущей стоимости в случае начисления по сложным процентам имеет следующий вид:

где PV — настоящая (приведенная) стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). Предполагается, что процентная ставка не изменяется в течение всего срока инвестирования; n – количество периодов времени, в течение которого начисляются проценты.

Про вычисление Будущей стоимости по сложным процентам можно прочитать в статье Сложные проценты в MS EXCEL . В этой статье разобраны случаи применения функции БС() и формула капитализации m раз в год. В статье Сложные проценты в MS EXCEL. Переменная ставка разобраны случаи применения функции БЗРАСПИС() для расчета будущей стоимости при переменной ставке. В статье Непрерывные проценты Будущая стоимость рассчитывается при непрерывном начислении процентов.

Аннуитет

Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Будущей стоимости существенно усложняется См. статью Аннуитет. Определяем в MS EXCEL Будущую Стоимость .

В случае, если сумма начальной инвестиции =0 и нужно определить Будущую стоимость периодических равновеликих платежей, то это можно сделать по формуле (см. файл примера ):

FV = PMT * (((1+i)^n)-1) / i

где PMT – размер платежа при аннуитете; i — процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц). В формуле предполагается, что проценты начисляются в конце периода; n – количество периодов времени, в течение которых начисляются проценты (и делаются платежи).

Источник

Аннуитет. Определяем в EXCEL Будущую Стоимость

history 2 февраля 2015 г.

Определим Будущую стоимость инвестиции в случае аннуитета. Под инвестицией будем понимать как регулярные взносы, так и начальный взнос. Для этого будем использовать функцию БС() . Также выведем альтернативную формулу для расчета Будущей стоимости.

Будущая стоимость (Future Value), является суммой, в которую в будущем превратится определенная сумма денег, инвестированная ранее под известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Будущей стоимости, также как и Текущей стоимости важен, так как, платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту. Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты: простые проценты , сложные проценты или аннуитет .

В MS EXCEL Будущая стоимость для аннуитета и для сложных процентов рассчитывается функцией БС() .

Примечание : в случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов (не аннуитет) используется функция БЗРАСПИС() .

Использование функции БС() в случае накопления вклада

Функция БС(ставка; кпер; плт; [пс]; [тип]) возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Например, если у Вас сейчас на банковском счете сумма ПС и вы ежемесячно дополнительно вносите одну и туже сумму ПЛТ, то функция вычислит сумму на Вашем банковском счете через Кпер месяцев. Теперь несколько замечаний:

Предполагается, что капитализация процентов происходит также периодически с процентной ставкой равной величине СТАВКА;
Процентная ставка указывается за период (если период равен месяцу, а задана годовая ставка =10%, то СТАВКА =10%/12);
По умолчанию аргумент Тип=0, т.е. пополняющие счет вклады делаются в конце каждого периода. Если Тип=1, то пополняющие счет вклады делаются в начале каждого периода;
Начальная сумма вклада ПС м.б. =0, но тогда суммы дополнительных взносов ПЛТ не должны быть =0;
Суммы дополнительных взносов м.б. =0, но тогда Начальная сумма вклада ПС не должна быть =0.

Примечание . Английский вариант функции: FV(rate, nper, pmt, [pv], [type]), т.е. Future Value – Будущая Стоимость.

Расчеты в БС() производятся по этой формуле:

Из формулы видно, будущая стоимость состоит из 2-х составляющих: будущая стоимость инвестиции ПС (вычисляется по формуле сложных процентов ) и будущая стоимость периодических равновеликих взносов ПЛТ (вычисляется по формуле аннуитета ).

Примечание . При БС=0 (начальная инвестиция =0) Будущая стоимость не зависит от параметра Тип.

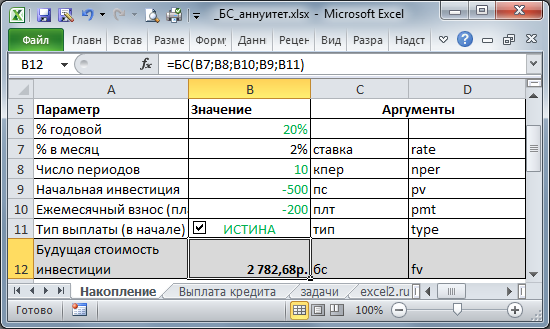
Вычислим Будущую стоимость в случае накопления вклада. Исходные данные приведены на рисунке ниже.

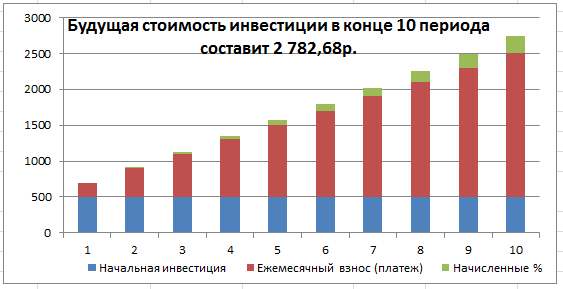
В результате расчетов получим следующий график накопления вклада (см. файл примера Лист Накопление ).

Примечание . Функцию БС() можно также использовать для вычисления баланса на конец периода (см. файл примера Лист Накопление, столбец G ). Для этого используйте выражение = БС(ставка; кпер; плт; [пс]; [тип])/ (1+ставка*тип)

Примечание . При Тип=1 (начисление процентов в начале периода), баланс на конец последнего периода не равен БС (как при Тип=0), т.к. учитывается начисление процентов на следующий день после окончания последнего периода! Т.е. к балансу на конец последнего периода прибавляется величина =БС(ставка; кпер; плт; [пс]; [тип])*ставка

Вывод формулы Будущей стоимости

Формула аннуитета может быть получена как сумма членов геометрической прогрессии, где знаменатель =(1+ставка). Выведем формулу аннуитета при Тип=0 в случае накопления вклада в течение Кпер периодов. Накопление вклада производится регулярными взносами (платежами) ПЛТ, начальная сумма вклада =0 (ПС). За период действует процентная ставка =Ставка. Итак, выводим:

Т.к. платеж вносится в конце периода, то в 1-й период проценты не начисляются (банк не использовал взнос). Баланс на конец периода =ПЛТ (взнос также сделан в конце периода).
В конце 2-го периода проценты начисляются на величину ПЛТ (на взнос, который был сделан в 1-м периоде). Баланс на конец 2-го периода =ПЛТ+ ПЛТ*ставка+ПЛТ= ПЛТ+ПЛТ*(1+ставка).
В конце 3-го периода проценты начисляются на величину ПЛТ+ ПЛТ *(1+ставка), т.е. на баланс начала 3-го периода (или на баланс конца 2-го периода, что естественно, то же самое). Баланс на конец 3-го периода = (ПЛТ+ ПЛТ *(1+ставка))*ставка+ (ПЛТ+ ПЛТ *(1+ставка))+ПЛТ=(ПЛТ+ ПЛТ *(1+ставка))*( 1+ставка) + ПЛТ= ПЛТ *(1+ставка)^2+ ПЛТ *(1+ставка)+ПЛТ.
Очевидно, что баланс в конце последнего периода (кпер)= ПЛТ *(1+ставка)^(кпер-1)+ ПЛТ *(1+ставка)^ (кпер -2)+… +ПЛТ *(1+ставка)^2+ ПЛТ *(1+ставка)+ПЛТ. Заметим, что ПЛТ = ПЛТ *(1+ставка)^0
Формула, полученная на предыдущем шаге, является суммой членов геометрической прогрессии и одновременно =БС: первый член геометрической прогрессии =ПЛТ, знаменатель =(1+ставка). Т.е. БС=ПЛТ*(1-(1+ставка)^ кпер)/(1-(1+ставка))= ПЛТ*(((1+ставка)^ кпер)-1)/ставка. Полученное уравнение с точностью до знака совпадает со вторым слагаемым формулы для вычисления БС (при Тип=0).

Как показано в файле примера (лист Накопление) при задании аргументов функции БС() у ПЛТ указывают знак минус (в этом случае БС>0). Противоположные знаки у ПЛТ и БС указывают на то, что мы имеем дело с разнонаправленными денежными потоками: БС – это деньги, которые банк вернет нам после окончания вклада, а -ПЛТ – это деньги, которые мы регулярно отдаем банку . Поэтому, окончательная формула для БС() (при ПС=0 и Тип=0): =- ПЛТ*(((1+ставка)^ кпер)-1)/ставка

Использование функции БС() в случае возврата кредита

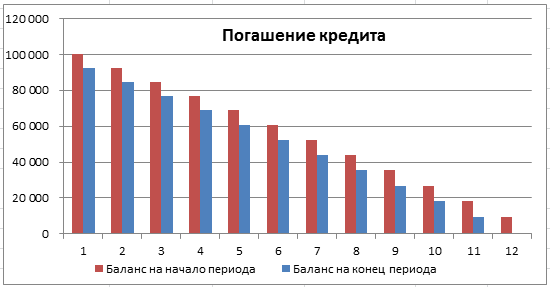
Функция БС() может быть использована также для нахождения остаточной стоимости ссуды по прошествии заданного количества периодов (см. файл примера Лист Выплата кредита ). Для этого используйте формулу =-БС(ставка; кпер; плт; [пс]; [тип])/ (1+ставка*тип)

При выплате кредита обычно предполагается, что по прошествии Кпер периодов (т.е. по истечению срока займа) Будущая стоимость кредита станет равна 0 (т.е. кредит будет полностью возращен).

Примечание : в файле примера приведено решение нескольких простых задач по определению Будущей стоимости.

Источник