Python bitcoin public key

Генерируем Bitcoin-адрес на Python

Тема криптовалют снова начинает будоражить интернет. Супер, что вам не надо идти в отделение банка с паспортом и выстаивать очередь, чтобы открыть счет. Сгенерировать кошелек Bitcoin — дело нескольких строк кода на Python.

Нам понадобятся библиотеки base58 и ecdsa. base58 – это кодирование бинарных данных 58-ю печатными символами (цифрами и латинскими буквами, кроме 0, O, I, l, которые похожи друг на друга). ecdsa – библиотека криптографии на эллиптических кривых.

Импортируем то, что нужно:

Нам нужен приватный ключ, из него мы вычислим публичный ключ, а из него – адрес кошелька Bitcoin. (Обратная процедура не возможна без полного перебора до конца времен). Приватный ключ – это 32 байта данных, которые мы получим из криптографически-надежного источника случайных чисел. Вообще можно придумать свой приватный ключ самостоятельно, если так хочется. Для генерации случайного приватного ключа мы воспользуемся библиотекой ecdsa:

Вычислим этой же библиотекой публичный ключ и добавим спереди байт 0x4 (это признак «несжатого» публичного ключа; есть и другие форматы).

Теперь нужно из публичного ключа сделать привычный число-буквенный адрес Bitcoin. Взглянем на схему:

Для получения адреса из публичного ключа вычисляем сначала RIPEMD160(SHA256(public-key)):

Дополняем его префиксом 0x0 (главная сеть Bitcoin):

Вычисляем контрольную сумму (нужна, чтобы наши денюжки не пропадали, если мы ошибемся в каком-то символе адреса). Контрольная сумма это первые 4 байта от SHA256(SHA256(r)):

Получаем адрес кошелька, закодировав в base58 сложенные r и checksum:

Генерация приватного ключа из своего источника случайностей, например, os.urandom:

Важно для конфиденциальных данных, вроде приватного ключа, использовать криптографически безопасный источник случайности. Об этом я писал в одной из недавних статей!

Полный пример кода генерации кошельков.

Проверить ключи и адрес можно здесь. (Нажимаем Skip, дальше Enter my own…)

Подробнее по теме можно почитать здесь.

Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈

Источник

circulosmeos / easy-bitcoin-address-from-public-key.py

#!/usr/bin/env python

# https://en.bitcoin.it/wiki/Protocol_documentation#Addresses

import hashlib

import base58

# ECDSA bitcoin Public Key

pubkey = ‘0450863ad64a87ae8a2fe83c1af1a8403cb53f53e486d8511dad8a04887e5b23522cd470243453a299fa9e77237716103abc11a1df38855ed6f2ee187e9c582ba6’

# See ‘compressed form’ at https://en.bitcoin.it/wiki/Protocol_documentation#Signatures

compress_pubkey = False

def hash160 ( hex_str ):

sha = hashlib . sha256 ()

rip = hashlib . new ( ‘ripemd160’ )

sha . update ( hex_str )

rip . update ( sha . digest () )

print ( «key_hash = \t » + rip . hexdigest () )

return rip . hexdigest () # .hexdigest() is hex ASCII

if ( compress_pubkey ):

if ( ord ( bytearray . fromhex ( pubkey [ — 2 :])) % 2 == 0 ):

pubkey_compressed = ’02’

else :

pubkey_compressed = ’03’

pubkey_compressed += pubkey [ 2 : 66 ]

hex_str = bytearray . fromhex ( pubkey_compressed )

else :

hex_str = bytearray . fromhex ( pubkey )

# Obtain key:

key_hash = ’00’ + hash160 ( hex_str )

# Obtain signature:

sha = hashlib . sha256 ()

sha . update ( bytearray . fromhex ( key_hash ) )

checksum = sha . digest ()

sha = hashlib . sha256 ()

sha . update ( checksum )

checksum = sha . hexdigest ()[ 0 : 8 ]

print ( «checksum = \t » + sha . hexdigest () )

print ( «key_hash + checksum = \t » + key_hash + ‘ ‘ + checksum )

print ( «bitcoin address = \t » + ( base58 . b58encode ( bytes ( bytearray . fromhex ( key_hash + checksum )) )). decode ( ‘utf-8’ ) )

This comment has been minimized.

Copy link Quote reply

circulosmeos commented May 5, 2018

See bitcoin-in-tiny-pieces for updated short Bitcoin scripts!

This comment has been minimized.

Copy link Quote reply

jiamijiang commented Apr 27, 2020

You can’t perform that action at this time.

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session.

Источник

Python bitcoin public key

This code is deprecated and should not be used

Python library with tools for Bitcoin and other cryptocurrencies.

Brainwallet-based Private Keys

Sending Transactions to Addresses

Sending OP_RETURN Transactions

Litecoin, Namecoin, Peercoin, Primecoin, Testnet, Worldcoin, Megacoin, Feathercoin, Terracoin, Novacoin, Dogecoin, Anoncoin, Protoshares, Ixcoin, Memorycoin, Infinitecoin, Cryptogenic Bullion, Quarkcoin, Netcoin, Earthcoin, Reddcoin, (insert your favorite cryptocurrency here)

Q: Can I contribute to pybitcoin?

A: Of course! Any and all are encouraged to contribute. Just fork a copy of the repo and get started on something that you think would improve the current offering.

Q: What should I work on?

A: That’s up to you! For a quick project, consider adding support for a new cryptocurrency (should only require two lines of code, not including the unit tests).

Meanwhile, for something a bit more ambitious, check the issues section for outstanding feature requests.

pybitcoin is still in beta. Developers using pybitcoin are encouraged to inspect the code for themselves and perform their own tests. We are committed to ensuring that this library behaves exactly as it is supposed to under all conditions, and have plans to ramp up our testing efforts going forward.

About

A Bitcoin python library for private + public keys, addresses, transactions, & RPC

Источник

Bitcoin in a nutshell — Cryptography

Одна из причин, почему Bitcoin продолжает привлекать столько внимания — это его исключительная «математичность». Сатоши Накамото удалось создать систему, которая способна функционировать при полном отсутствии доверия между ее участниками. Все взаимодействия основаны на строгой математике, никакого человеческого фактора — вот в чем была революционность идеи, а не в одноранговой сети, как многие думают. Поэтому первую главу я решил посвятить именно математическим основам Bitcoin.

Ниже я постараюсь объяснить вам самые базовые вещи — эллиптические кривые, ECC, приватные / публичные ключи и так далее. По возможности я буду иллюстрировать свои слова примерами кода, преимущественно на Python 2.7, если что-то непонятно — спрашивайте в комментариях.

Table of content

Introduction

Как я уже сказал выше, криптография — это фундаментальная часть Bitcoin. Без нее вообще бы ничего не заработало, поэтому начинать нужно именно отсюда.

В Bitcoin используется так называемая криптография на эллиптических кривых (Elliptic curve cryptography, ECC). Она основана на некоторой особой функции — эллиптической кривой (не путать с эллипсом). Что это за функция и чем она так примечательна я расскажу дальше.

Elliptic curve

Эллипти́ческая крива́я над полем — неособая кубическая кривая на проективной плоскости над (алгебраическим замыканием поля ), задаваемая уравнением 3-й степени с коэффициентами из поля и «точкой на бесконечности» — Wikipedia

Если на пальцах, то эллиптическая кривая — это внешне довольно простая функция, как правило, записываемая в виде так называемой формы Вейерштрасса:

В зависимости от значений параметров и , график данной функции может выглядеть по разному:

Скрипт для отрисовки графика на Python:

Если верить вики, то впервые эта функция засветилась еще в трудах Диофанта, а позже, в 17 веке, ей заинтересовался сам Ньютон. Его исследования во многом привели к формулам сложения точек на эллиптической кривой, с которыми мы сейчас познакомимся. Здесь и в дальнейшем мы будем рассматривать некоторую эллиптическую кривую .

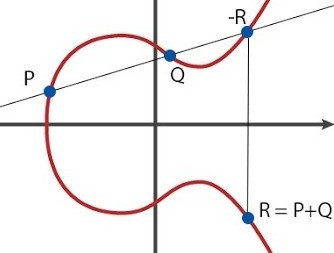
Пусть есть две точки . Их суммой называется точка , которая в простейшем случае определяется следующим образом: проведем прямую через и — она пересечет кривую в единственной точке, назовем ее . Поменяв координату точки на противоположную по знаку, мы получим точку , которую и будем называть суммой и , то есть .

Считаю необходимым отметить, что мы именно вводим такую операцию сложения — если вы будете складывать точки в привычном понимании, то есть складывая соответствующие координаты, то получите совсем другую точку , которая, скорее всего, не имеет ничего общего с или и вообще не лежит на кривой .

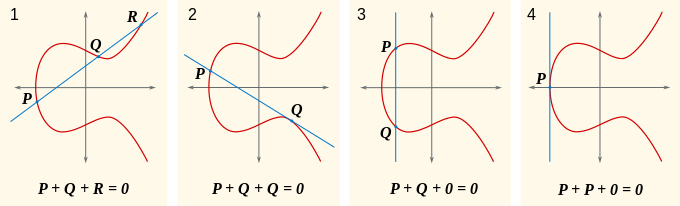
Самые сообразительные уже задались вопросом — а что будет, если например провести прямую через две точки, имеющие координаты вида и , то есть прямая, проходящая через них, будет параллельна оси ординат (третий кадр на картинке ниже).

Несложно увидеть, что в этом случае отсутствует третье пересечение с кривой , которое мы называли . Для того, чтобы избежать этого казуса, введем так называемую точку в бесконечности (point of infinity), обозначаемую обычно или просто , как на картинке. И будем говорить, что в случае отсутствия пересечения .

Особый интерес для нас представляет случай, когда мы хотим сложить точку саму с собой (2 кадр, точка ). В этом случае просто проведем касательную к точке и отразим полученную точку пересечения относительно .

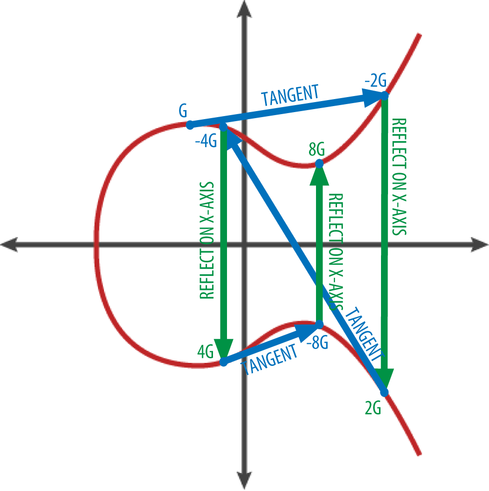
Теперь, легким движением руки, можно ввести операцию умножения точки на какое-то число. В результате получим новую точку , то есть раз. С картинкой все должно стать вообще понятно:

Elliptic curve over a finite field

В ECC используется точно такая же кривая, только рассматриваемая над некоторым конечным полем — простое число. То есть

Все названные свойства (сложение, умножение, точка в бесконечности) для такой функции остаются в силе, хотя, если попробовать нарисовать данную функцию, то напоминать привычную эллиптическую кривую она будет лишь отдаленно (в лучшем случае). А понятие «касательной к функции в точке» вообще теряет всякий смысл, но это ничего страшного. Вот пример функции для :

А вот для , тут вообще почти хаотичный набор точек. Единственное, что все еще напоминает о происхождении этого графика, так это симметрия относительно оси .

P. S. Если вам интересно, как в случае с кривой над конечным полем вычислить координаты точки , зная координаты и — можете полистать «An Introduction to Bitcoin, Elliptic Curves and the Mathematics of ECDSA» by N. Mistry, там все подробно расписано, достаточно знать математику на уровне 8 класса.

P.P.S. На случай, если мои примеры не удовлетворили ваш пытливый ум, вот сайт для рисования кривых всех сортов, поэкспериментируйте.

SECP256k1

Возвращаясь к Bitcoin, в нем используется кривая SECP256k1. Она имеет вид и рассматривается над полем , где — очень большое простое число, а именно .

Так же для SECP256k1 определена так называемая base point, она же generator point — это просто точка, как правило, обозначаемая , лежащая на данной кривой. Она нужна для создания публичного ключа, о котором будет рассказано ниже.

Простой пример: используя Python, проверим, принадлежит ли точка кривой SECP256k1

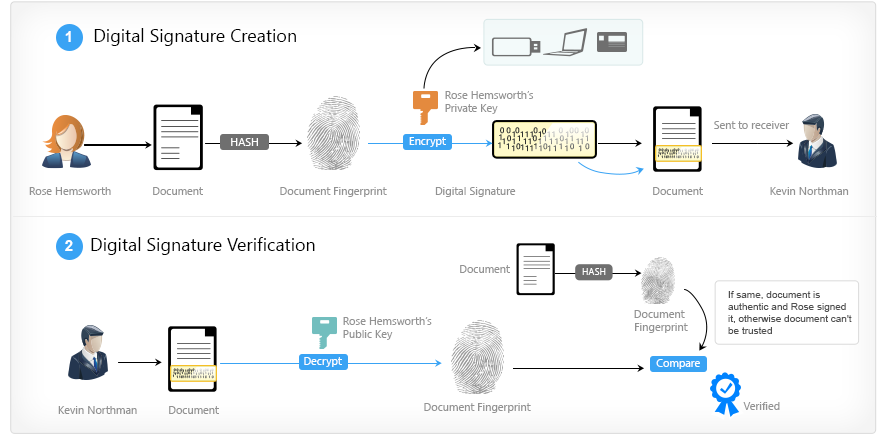
Digital signature

Электро́нная по́дпись (ЭП), Электро́нная цифровая по́дпись (ЭЦП) — реквизит электронного документа, полученный в результате криптографического преобразования информации с использованием закрытого ключа подписи и позволяющий проверить отсутствие искажения информации в электронном документе с момента формирования подписи (целостность), принадлежность подписи владельцу сертификата ключа подписи (авторство), а в случае успешной проверки подтвердить факт подписания электронного документа (неотказуемость) — Wikipedia

Общая идея такая: Алиса хочет перевести 1 BTC Бобу. Для этого она создает сообщение типа:

Потом Алиса берет свой приватный ключ (пока что можете считать, что это число, известное только Алисе), хэш сообщения и функцию вида . На выходе она получает подпись своего сообщения — в случае ECDSA это будет пара целых чисел, для других алгоритмов подпись может выглядеть по другому. После этого она рассылает всем участникам сети исходное сообщение, подпись и свой публичный ключ.

В результате, каждый Вася при желании сможет взять эту троицу, функцию вида и проверить, действительно ли владелец приватного ключа подписывал это сообщение или нет. А если внутри сети все знают, что принадлежит Алисе, то можно понять, отправила эти деньги она или же кто-то пытается сделать это от ее имени.

Более того, предположим, что нашелся человек, вставший между Алисой и остальной сетью. Пусть он перехватил сообщение Алисы и что-то в нем изменил, буквально 1 бит из миллиарда. Но даже в этом случае проверка подписи на валидность покажет, что сообщение было изменено.

Это очень важная фича для Bitcoin, потому как сеть распределенная. Мы не можем заранее знать, к кому попадет наша транзакция с требованием перевести 1000 BTC. Но изменить ее (например указать свой адрес с качестве получателя) он не сможет, потому как транзакция подписана вашим приватным ключом, и остальные участники сети сразу поймут, что здесь что-то не так.

AHTUNG! В действительности процесс довольно сильно отличается от вышеописанного. Здесь я просто на пальцах показал, что из себя представляет электронно-цифровая подпись и зачем она нужна. Реальный алгоритм описан в главе «Bitcoin in a nutshell — Transactions».

Private key

Приватный ключ — это довольно общий термин и в различных алгоритмах электронной подписи могут использоваться различные типы приватных ключей.

Как вы уже могли заметить, в Bitcoin используется алгоритм ECDSA — в его случае приватный ключ — это некоторое натуральное 256 битное число, то есть самое обычное целое число от до . Технически, даже число 123456 будет являться корректным приватным ключом, но очень скоро вы узнаете, что ваши монеты «принадлежат» вам ровно до того момента, как у злоумышленника окажется ваш приватный ключ, а значения типа 123456 очень легко перебираются.

Важно отметить, на сегодняшний день перебрать все ключи невозможно в силу того, что — это фантастически большое число.

Постараемся его представить: согласно этой статье, на всей Земле немногим меньше песчинок. Воспользуемся тем, что , то есть песчинок. А всего адресов у нас , примерно .

Значит, мы можем взять весь песок на Земле, превратить каждую песчинку в новую Землю, в получившейся куче планет каждую песчинку на каждой планете снова превратить в новую Землю, и суммарное число песчинок все равно будет на порядки меньше числа возможных приватных ключей.

По этой же причине большинство Bitcoin клиентов при создании приватного ключа просто берут 256 случайных бит — вероятность коллизии крайне мала.

Python

Python, ECDSA

Bitcoin-cli

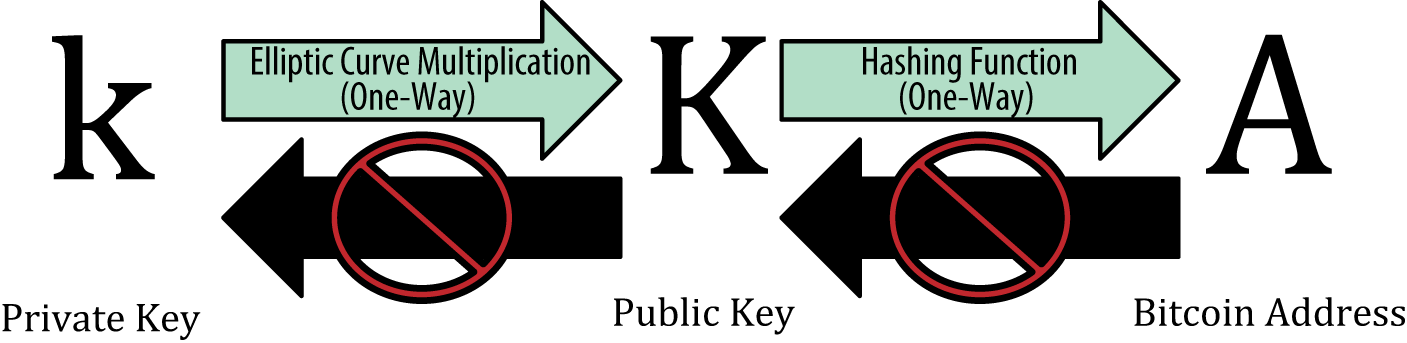
Public key

Пусть — наш приватный ключ, — base point, тогда публичный ключ . То есть, фактически, публичный ключ — это некоторая точка, лежащая на кривой SECP256k1.

Два важных нюанса. Во-первых, несложно видеть, что операция получения публичного ключа определена однозначно, то есть конкретному приватному ключу всегда соответствует один единственный публичный ключ. Во-вторых, обратная операция является вычислительно трудной и, в общем случае, получить приватный ключ из публичного можно только полным перебором первого.

Ниже вы узнаете, что точно такая же связь существует между публичным ключом и адресом, только там все дело в необратимости хэш-функций.

Python, ECDSA

C++, libbitcoin

Для компиляции и запуска используем (предварительно установив libbitcoin):

Вы можете видеть, что форматы публичных ключей в первом и втором примере отличаются (как минимум длиной), об этом я подробнее расскажу ниже.

Formats & address

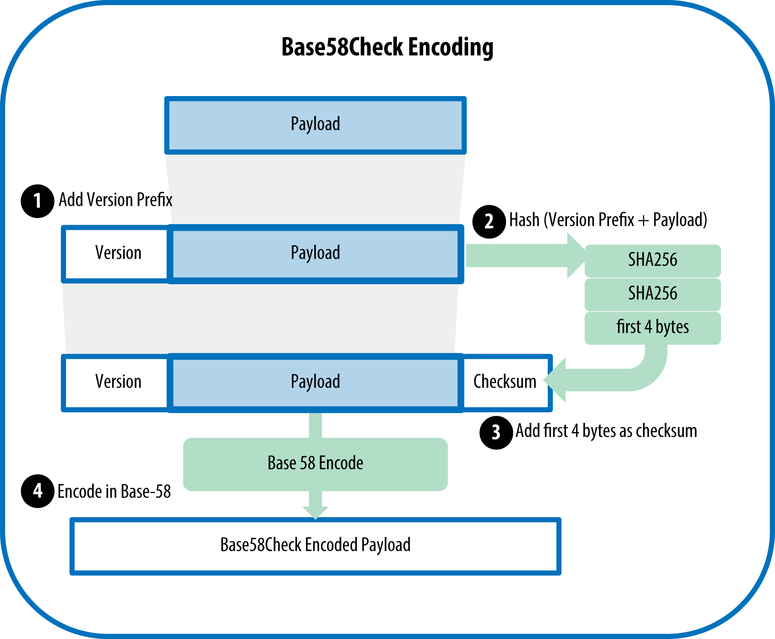
Base58Check encoding

Эта кодировка будет встречаться нам постоянно на протяжении всей книги, поэтому стоит понимать, как она работает и зачем она вообще нужна.

Ее суть в том, чтобы максимально кратко записать последовательность байт в удобочитаемом формате и при этом сделать вероятность возможных опечаток еще меньше. Я думаю вы сами понимаете, что в случае Bitcoin безопасность лишней не бывает. Один неправильный символ и деньги уйдут на адрес, ключей к которому скорее всего никто никогда не найдет. Вот комментарий к этой кодировке из в base58.h:

Краткость записи проще всего реализовать, используя довольно распространенную кодировку Base64, то есть используя систему счисления с основанием 64, где для записи используются цифры 0,1. 9 , буквы a-z и A-Z — это дает 62 символа, оставшиеся два могут быть чем угодно, в зависимости от реализации.

Первое отличие Base58Check в том, что убраны символы 0,O,l,I на случай, если кто-нибудь решит их перепутать. Получается 58 символов, можете проверить

Второе отличие — это тот самый check. В конец строки снова добавляется checksum — первые 4 байта SHA256(SHA256(str)) . Ну и еще нужно добавить в начало столько единиц, сколько ведущих нулей было до кодировки в base58, это уже дело техники.

Private key formats

Самый очевидный способ хранить приватный ключ — это записать 256 бит в виде кучи нулей и единиц. Но, наверное, любой технически грамотный человек понимает, что будет сильно проще представить ту же самую последовательность в виде 32 байт, где каждому байту соответствует два символа в шестнадцатиричной записи. Напомню, что в этом случае используются цифры 0,1. 9 и буквы A,B,C,D,E,F . Этот формат я использовал в примерах выше, для красоты его еще иногда разделяют пробелами.

Другой более прогрессивный формат — WIF (Wallet Import Format). Строится он довольно просто:

1. Берем приватный ключ, например 0C28FCA386C7A227600B2FE50B7CAE11EC86D3BF1FBE471BE89827E19D72AA1D
2. Записываем его в Base58Check с префиксом 0x80 . Все.

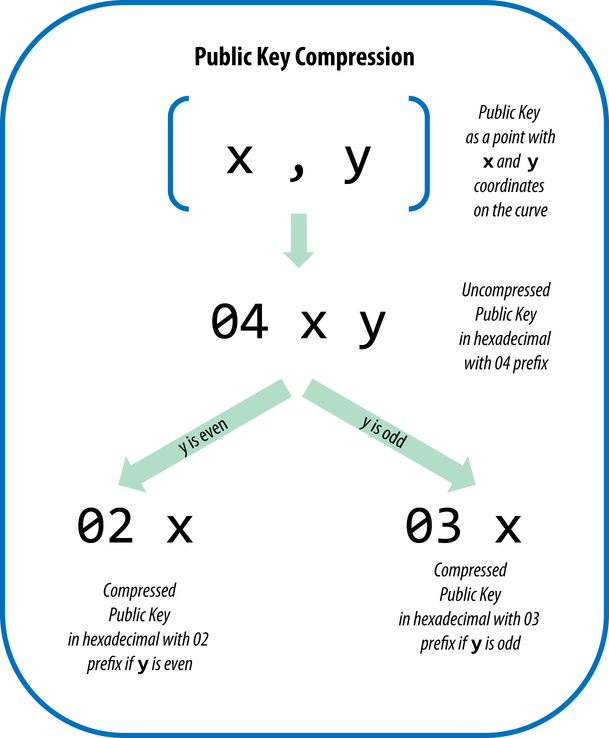
Public key formats

На всякий случай напомню, что публичный ключ — это просто точка на прямой SECP256k1. Первый и самый распространенный вариант его записи — uncompressed формат, по 32 байта для X и Y координат. Чтобы не возникало путаницы, используется префикс 0x04 и того 65 байт.

Однако, как можно догадаться из названия, это не самый оптимальный способ хранить публичный ключ.

Вы удивитесь, но второй формат называется compressed. Суть его в следующем: публичный ключ — это точка на кривой, то есть пара чисел удовлетворяющая уравнению . А значит можно записать только Х координату и если нам понадобится Y координата — просто решаем уравнение. Тем самым мы уменьшаем размер публичного ключа почти на 50%!

Единственный нюанс — если точка лежит на кривой, то для ее Х координаты очевидно существует два решения такого уравнения (посмотрите на графики выше, если сомневаетесь). Обычно мы бы просто сохранили знак для Y координаты, но когда речь идет о функции над конечным полем, то нужно воспользоваться следующим свойством: если для Х координаты существуют решения уравнения, то одна из точек будет иметь четную Y координату, а вторая — нечетную (опять же, можете сами в этом убедиться).

В первом случае используется префикс 0x02 , во втором — 0x03 . Вот иллюстрация процесса:

Address

Как уже было сказано, адрес получается из публичного ключа однозначным образом. Более того, провести обратную операцию невозможно, так как используются криптографически стойкие хэш функции — RIPEMD160 и SHA256. Вот алгоритм перевода публичного ключа в адрес:

1. Возьмем приватный ключ, например 45b0c38fa54766354cf3409d38b873255dfa9ed3407a542ba48eb9cab9dfca67
2. Получим из него публичный ключ в uncompressed формате, в данном случае это 04162ebcd38c90b56fbdb4b0390695afb471c944a6003cb334bbf030a89c42b584f089012beb4842483692bdff9fcab8676fed42c47bffb081001209079bbcb8db .
3. Считаем RIPEMD160(SHA256(public_key)) , получается 5879DB1D96FC29B2A6BDC593E67EDD2C5876F64C
4. Переводим результат в Base58Check с префиксом 0x00 — 17JdJpDyu3tB5GD3jwZP784W5KbRdfb84X . Это и есть адрес.

Sign & verify

Не думаю, что вам нужно обязательно знать технические подробности того, как именно ECDSA подписывает и проверяет сообщения, все равно вы везде будете пользоваться готовыми библиотеками. Главное, чтобы у вас было общее понимание того зачем это нужно, но если вам все таки интересно — полистайте Layman’s Guide to Elliptic Curve Digital Signatures, там внизу есть красивая визуализация всего процесса, можете сами попробовать.

У меня на этом все, следующая глава: Bitcoin in a nutshell — Transaction.

Источник