При временных лагах инвестиции

Учет фактора времени при определении лагов капитальных вложений

Страницы работы

Содержание работы

1.1.Учет фактора времени при определении лагов капитальных вложений

Лаги капитальных вложений играют большую роль при анализе процесса воспроизводства фондов и оценке эффективности использования капитальных вложений. Они характеризуют временной разрыв между осуществлением вложений и вводом в действие созданных фондов.

Оценка этого запаздывания на народнохозяйственном уровне в принципе требует агрегации и усреднения информации об индивидуальных строительных циклах во всех отраслях народного хозяйства и поэтому является весьма сложной, а часто (при отсутствии необходимой информации) и нереализуемой процедурой. Поэтому широкое применение нашли различного рода лаговые модели инвестиционного процесса.

Достаточно общая форма уравнения, отражающая распределенный характер связи с между капитальными вложениями и вводом в действие фондов, имеет вид [157]

Ф(t)=t(t), (3.46)

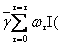
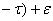
где Ф(t) — объем вводимых в t-м году фондов;

τ — продолжительность лага, который может принимать значения от 0 до τ _тах;

I (t- τ) — производственные капитальные вложения, соответствующие лагу τ,

ω_τ — коэффициент лагового распределения, который показывает долю капитальных вложений года (t— τ), входящую в состав вводов фондов года t;

γ— доля фондообразующих капитальных вложений в их общем объеме;

ε (t) — ошибка уравнения.

На основе (3.46) могут быть определены различные лаговые характеристики, в частности инвестиционный и строительный лаги [14, 157]. При этом под инвестиционным лагом понимается средний срок пребывания капитальных вложений в незавершенном строительстве, т. е. время их одного оборота; под строительным же лагом понимается продолжительность проведения строительно-монтажных работ, причем обычно подразумевается средняя продолжительность сооружения объектов.

При проведении расчетов сравнительной эффективности различных вариантов строительства производственных объектов, выборе их оптимальной продолжительности и динамики освоения затрат в ходе строительства часто строительный лаг понимается в следующем близком к определенному выше инвестиционному лагу смысле.

Источник

Прогнозирование динамики с учетом временного лага

В экономике существует довольно большая группа процессов и явлений, в развитии которых причина на тот или иной временной интервал опережает следствие. Это отражает инерционность многих экономических процессов и необходимость «созревания» предпосылок. Примеров подобных зависимостей множество:

■ средства, потраченные торговой фирмой на закупку товара, принесут прибыль только после его продажи;

■ капитал, финансированный в новое оборудование, послужит причиной увеличения объема выпуска продукции после ввода и освое­ния оборудования;

■ выдача патента на изобретение опережает на несколько лет начало его коммерческого использования;

■ затраты на маркетинг, рекламу, повышение квалификации ра­ботников не сразу могут послужить основанием для улучшения резуль­татов работы предприятия.

Временным лагом (τ) принято называть промежуток времени, по истечении которого изменение показателей одного временного ряда оказывает влияние на показатели другого. Корреляционно-регресси­онная зависимость с учетом временного лага может быть описана следующим уравнением:

Авторегрессионной называют модель, в которой лаговое соотно­шение связывает значение одного и того же показателя в разные мо­менты времени:

Рассмотрим некоторые процессы, в динамике которых наблюдается разрыв во времени между причиной и следствием. К их числу в первую очередь следует отнести инвестирование. Инвестиционным лагом называют срок пребывания инвестиций в незавершенном строитель­стве, он охватывает период от начала проектирования объекта до его ввода в действие на полную мощность. В составе инвестиционного лага иногда выделяют строительный лаг — период от начала строительства до ввода объекта в действие на полную мощность.

Оценивая инвестиционный лаг, следует помнить о технологиче­ской неоднородности инвестиций, в силу которой временной лаг по раз­ным группам инвестиций будет значительно различаться. Для немонтируемого оборудования (например, транспортных средств) временной лаг между направлением инвестиций и вводом оборудования в действие близок к нулю, для оборудования монтируемого — обычно меньше года, а для строительно-монтажных работ, как правило, более года. Поэтому модели инвестиционного процесса, построенные с учетом временного лага, должны не только дать их среднюю оценку, но и описать распре­деление инвестиций по годам на протяжении инвестиционного или строительного цикла. Исходными данными в таких моделях будет за­данная динамика инвестиций, а результирующими, прогнозируемы­ми, — динамика ввода в действие основных фондов.

В социально-экономическом прогнозировании определенную роль играет также оценка демографических лагов, под которыми пони­мают период от рождения до вступления в трудоспособный возраст и начала трудовой деятельности после получения образования и про­фессиональной подготовки.

Одно из направлений активного использования подобных мето­дов корреляционного анализа — поиск индикаторов, которые способ­ны заблаговременно предупредить о возможных изменениях в движе­нии цен. В различные периоды в качестве индикаторов предлагались следующие показатели:

■ движение цены на золото (традиционно она отражала инфля­ционные ожидания, так как покупка драгоценного металла была попу­лярным средством страхования от возможных, финансовых рисков, но сейчас свопы (торгово-финансовые обменные операции) и опционы (приобретение права на совершение будущей сделки; например, право приобрести или продать ценные бумаги по определенной цене в определенный будущий момент времени либо в течение определенного будущего срока) обеспечивают более надежные гарантии от инфляции);

■ различные индексы цен на сырьевые товары (удорожание или удешевление сырья практически сразу сказывается на стоимости гото­вой продукции). Многочисленные исследования динамики цен на сы­рьевые товары и инфляции в промышленно развитых странах показа­ли, что в 1970—1990-е гг. увеличение инфляции следовало за скачком цен на сырье с отрывом в один год.

Аналогичный принцип лежит и в основе анализа и прогнозиро­вания конъюнктуры рынка с помощью экономических барометров. Экономический барометр — это система экономических показателей, применяемых для анализа и прогнозирования конъюнктуры рынка. Все показатели делятся на три группы: опережающие (лидирующие), со­впадающие (синхронные) и запаздывающие.

Гарвардский барометр (и построенные по его образу) измеряет­ся лагами между изменениями среднеарифметических величин для показателей каждой группы. Все ряды выравниваются путем деления, каждого показателя на его среднеквадратическое отклонение от трен­да. Зная точку циклического минимума или максимума лидирующей группы, барометр предсказывает, что через период времени, равный среднему лагу за несколько прошлых циклов, наступит соответствую­щая точка для показателей совпадающей и запаздывающей групп.

Среди опережающих показателей называют среднюю продолжи­тельность рабочей недели в промышленности, число вновь создавае­мых деловых предприятий, среднее число сверхурочных часов; среди совпадающих — личный доход за вычетом трансфертных платежей, ВНП, уровень безработицы; среди запаздывающих — численность безработных, удельные расходы на заработную плату, изменение индекса потребительских цен и т.п.

Во многих прогнозах ставится вопрос не о запаздывании, а об упреждении событий. Так, нас может интересовать, когда и какие ин­вестиции необходимо осуществить, чтобы произвести в прогнозном году определенное количество продукции, на сколько и когда следует расширить посевные площади под определенную сельскохозяйствен­ную культуру, чтобы получить в прогнозном году необходимый уро­жай. В данном случае по предположению принимается прогнозное зна­чение y_t и рассчитывается необходимая величина x_t—τ.

Задание.На основе исходной информации о взаимосвязи иссле­дуемых показателей (в соответствии с заданием, определенным препо­давателем) выявить тесноту и характер их взаимосвязи и составить точечный и интервальный прогноз на заданный период времени. Спра­вочная информация к практической работе находится в табл. 5.1.

Таблица 5.1 Статистические функции табличного редактора Excel

Обозначение	Содержание расчетов
КОРРЕЛ	Возвращает коэффициент корреляции между двумя массивами данных
ЛИНЕЙН	Возвращает параметры линейного приближения по методу наименьших квадратов
ТЕНДЕНЦИЯ	Возвращает значения в соответствие с линейной аппроксимацией по методу наименьших квадратов
ЛГРФПРИБЛ	Возвращает параметры экспоненциального приближения по методу наименьших квадратов
РОСТ	Возвращает параметры экспоненциального приближения по методу наименьших квадратов, проекции по экспоненциальному прибли­жению

Задача 1. Продавец товара А анализирует информацию о цене товара и количестве продаж (табл. 3.2).

Таблица 3.2 Исходные данные

Количество, ед./дн.

Цена, руб.

Требуется вычислить коэффициент корреляции; построить мо­дель линейной регрессии и объяснить значения коэффициентов; рас­считать прогноз объема продаж при цене 4500, 3000 и 2500 руб.; опре­делить границы доверительного интервала.

Задача 2. В таблице 5.3 представлены данные о расходах на рекламу и то­варообороте шести предприятий оптовой торговли.

Таблица 3.3 Исходныеданные

Расходы на рекламу, тыс. руб.

Товарооборот, тыс. руб.

Требуется вычислить коэффициент корреляции; построить модель линейной регрессии и объяснить значения коэффициентов; рас­считать прогноз товарооборота при прогнозируемых расходах на рек­ламу в размере 75, 50 и 100 тыс. руб.; определить границы доверитель­ного интервала.

Задача 3. На основе статистических данных о средних ценах производи­телей основных видов топливно-энергетических ресурсов оцените степень влияния цены на нефть на цены других ресурсов (бензин автомобильный, топливо дизельное, мазут топочный); сделайте вывод о возможности ис­пользования прогноза цены нефти для разработки прогнозов цен на бен­зин автомобильный, топливо дизельное, мазут топочный; при обнару­жении зависимости рассчитайте прогнозные значения цен на названные топливно-энергетические ресурсы при условии, что в прогнозном пе­риоде цена нефти составит 5000 руб. за тонну (табл. 5.4).

Средние цены производителей основных видов

топливно-энергетических ресурсов, руб. за т

Вид топливное энергетических ресурсов	Период измерения
Нефть	6,3
Бензин автомобильный	18,3
Топливо дизельное	16,0

Мазут топочный 8,3 284 2244 1420 2102 1945 1927

Задача 4. На основании данных в таблице 5.5 проанализируйте тенденцию развития ЖД и других видов транспорта до 2015 года

Источник

При временных лагах инвестиции

Инвестиционный лаг

Таким образом, расчетный период (база для сопоставления) должен быть отдален от момента принятия решения о капитальных вложениях на величину инвестиционного лага, включающего длительности цикла проектирования, ожидания включения стройки в план капитального строительства, период строительства и освоения. Для среднего по мощности промышленного предприятия общая величина инвестиционного цикла в настоящее время составляет 8,5—10 лет, из которых около 3 лет уходит на разработку, экспертизу и утверждение проекта 4—4,5 года — на строительство 1—2 года — на освоение предприятием проектных показателей. [c.103]

Для того чтобы новые предприятия не ухудшали показатели действующего производства, необходимо сравнивать технико-экономические показатели проектируемых предприятий (коэффициент общей эффективности капитальных вложений, приведенные затраты, показатели производительности труда и фондоотдачи) не с соответствующими параметрами действующего производства на момент принятия решения о капитальных вложениях, а с перспективными отраслевыми показателями, сдвинутыми на величину инвестиционного лага. [c.104]

При расчетах показателей общей экономической эффективности капитальных вложений необходимо учитывать разрыв во времени (лаг) между осуществлением капитальных вложений и получением полезного эффекта. Средняя величина лага в нефтегазодобывающей отрасли составляет 1 год, в трубопроводном транспорте — более 4 лет. Методические положения по определению инвестиционного лага приведены в следующем разделе. [c.118]

В некоторых случаях, как уже отмечалось, при определении показателей общей (абсолютной) экономической эффективности капитальных вложений необходимо учитывать разрыв во времени (лаг) между осуществлением затрат и получением эффекта (прибыли, снижения себестоимости и т. д.). Учет лага при определении общей эффективности капитальных вложений данного периода осуществляется путем отнесения к ним прибыли, отстоящей от этого периода на величину лага. Инвестиционный лаг состоит из строительного лага — среднего времени для перевода всех авансированных в период строительства капитальных вложений в основные фонды и производственные мощности, и лага освоения — среднего времени, необходимого для достижения предусмотренной проектом мощности и технико-экономических показателей. [c.129]

Определить полный инвестиционный лаг по двум газоперерабатывающим заводам. Исходные данные приведены в табл. 92 [c.133]

Другой тип модели экономического роста представляет модель, предложенная лауреатом Нобелевской премии Р. Солоу. По сравнению с уже рассмотренной моделью роста модель Солоу позволяет более точно описать некоторые особенности макроэкономических процессов. Во-первых, производственная функция в этой модели нелинейна и обладает свойством убывания предельной производительности. Во-вторых, модель учитывает выбытие основного капитала. В-третьих, в модель Солоу включается описание динамики трудовых ресурсов и технического прогресса и их влияние на экономический рост. В-четвертых, здесь ставится и решается задача максимизации уровня потребления на некотором множестве устойчивых траекторий. Все это, конечно, усложняет структуру модели, и получение точных формул для траекторий изменения основных ее показателей становится существенно более сложной задачей. Поэтому некоторые другие аспекты описываются в базовой модели Солоу упрощенно например, считаются постоянными норма сбережений и норма выбытия капитала, инвестиционные лаги отсутствуют, а производственная функция имеет постоянную отдачу от масштаба. Кроме того, на начальном уровне анализа модели ищутся не траектории изменения всех ее показателей (как в модели Харрода-Домара), а характеристики состояний устойчивого равновесия, к которым система выходит в долгосрочном периоде. С формальной точки зрения это представляет собой существенно более простую задачу. [c.209]

Пусть р- цена готовой продукции, р — цена единицы инвестиционных благ, w- ставка заработной платы. Будем считать, что норма амортизации постоянна и равна d. Пусть инвестиционный лаг равняется одному периоду, то есть, инвестиции, осуществленные в период t, трансформируются в капитал и могут быть использованы в процессе производства в следующем периоде t+1. При этих условиях прибыль фирмы (до выплаты дивидендов) в период t (

Источник