Что такое корреляция акций и облигаций?
Объясните, пожалуйста, простым языком, что такое корреляция ценных бумаг? Почему о ней говорят при составлении портфеля и что значит, когда она отрицательная?
Корреляция показывает, насколько активы схожи по поведению. Показатель описывает закономерности. Например, если при росте одного актива другой дешевеет и эта закономерность подтверждается историческими данными, говорят, что у активов обратная корреляция. Это относится как к отдельным ценным бумагам, так и к широким рынкам, классам активов и секторам экономики.
Коэффициент корреляции вычисляется на конкретном историческом отрезке. Он обозначается буквой r и принимает значения от −1 до +1. Если два актива движутся в связке, то коэффициент корреляции будет ближе к +1, а если в противоположных направлениях — ближе к −1. Но когда корреляция близка к нулю, взаимосвязи между ними нет. Это значит, что при росте или падении одного актива другой может вообще никак себя не проявлять. Например, корреляция акций и облигаций на рынке США в период с 1950 по 2012 год составила 0,11.
Расскажу, как можно использовать знание о корреляции при формировании портфеля.
Роль корреляции в управлении портфелем
Понимание корреляции между инструментами позволяет диверсифицировать портфель и снизить инвестиционные риски.
Например, если инвестор собрал портфель из 10 нефтегазовых компаний, он защитил себя только от специфических рисков, связанных с конкретным эмитентом. Волатильность портфеля по-прежнему будет высокой: если цены на нефть упадут, портфель также уйдет в красную зону из-за тесной корреляции акций.
Чтобы диверсификация работала, необходимо использовать инструменты с низкой или обратной корреляцией. Тогда движение цены одного актива будет компенсироваться движением другого. Так, государственные облигации — наиболее частный диверсификатор для акций, поскольку у этих активов исторически низкая взаимосвязь друг с другом.
Таким же образом устроен и механизм хеджирования, когда инвестор открывает позицию с отрицательной корреляцией к исходному активу, чтобы застраховаться от его падения. Например, так называемые обратные ETF обладают корреляцией, близкой к −1 по отношению к исходному активу.
Источник
Оценка риска и доходности портфеля
Пусть портфель сформирован из двух рисковых активов, например акций фирм «А» и «В», характеристики которых представлены в табл. 9.1. Определим доходность и риск портфеля АВ.
Характеристики портфеля АВ
Состав Доходность К,
% Доля в портфеле
Актив А 5 20 2/3
Актив В 15 40 1/3
Доходность данного портфеля может быть определена по формуле
ЛАВ = ХаЛа +ХвКв, (9.1)
где ХА, Хв — доля соответствующего актива в портфеле;
средняя ожидаемая доходность активов Аж В.
Для рассматриваемого примера средняя ожидаемая доходность портфеля
(0,05 х 2 / 3) + (0,15 х 2 / 3) = 0,0833, или 8,33%.
Как и для отдельного актива, риск портфеля измеряется по-казателями, характеризующими изменчивость его доходности,
например дисперсией а2 или стандартным отклонением а.
Для оценки взаимосвязи изменений двух переменных в тео-рии вероятностей и математической статистике используются два показателя: ковариация и корреляция.
Ковариация характеризует взаимную изменчивость двух по-казателей.
СОУ(ИА КВ)=САВ =^(ЯЛ-ВГАШв,Ю(9.2)
Положительная ковариация означает, что доходности двух активов изменяются в среднем в одном направлении, а отрица-тельная — в противоположном.
Понятие корреляции двух показателей аналогично понятию их ковариации. Коэффициент корреляции является производ-ным показателем от ковариации и вычисляется делением (нор-мированием) последней на произведение соответствующих стандартных отклонений:
СОУ(КА, Яв) р** = = ТТ»!“(9*3)
Коэффициент корреляции принимает значение в фиксиро-ванном диапазоне от —1 до +1 и поэтому более удобен и нагля-ден в интерпретации.
При этом значение р = 1 (полная положительная корреля-ция) означает существование линейной зависимости между из-менениями двух показателей. Нетрудно заметить, что доход-ность любого актива полностью положительно коррелирована сама с собой.
В случае р = — 1 (полная отрицательная корреляция) между изменениями показателей существует обратная линейная взаи-мосвязь.
Если р = 0 (отсутствие корреляции), считается, что показатели изменяются независимо один от другого.
Понятия ковариации и корреляции играют важнейшую роль в определении риска портфеля и теории инвестиций в целом. В частности, с учетом возможных взаимосвязей доходностей риск портфеля из двух активов Ал В может быть определен по следующей формуле:
(ЗАВ = Л1^А°А +Хв оо первое слагаемое в (9.13) будет стремиться к 0, а второе — к величине рст2.
Таким образом, несмотря на диверсификацию, минималь-ный риск такого портфеля остается равным Од/р.
Это свидетельствует о том, что для портфеля из положительно коррелированных активов (0
Рис. 9.6. Множество доступных портфелей и эффективная граница
ка) и Z(портфель с наибольшим уровнем доходности). Этот участок образует эффективную границу Марковица. Портфели, лежащие ниже точки Е и за точкой Z9 а также в любой точке плоскости допустимого множества, не являются эффективными. Рассмотрим в качестве примера портфель N. Как следует из рис. 9.6, этот портфель не может быть эффективным по критерию риск — доходность, поскольку портфель Ех обеспечивает ту же доходность, но при значительно меньшем уровне риска, а портфель Е2 дает возможность получить бблыпую доходность при том же уровне риска.
Какой именно портфель выберет инвестор, зависит от его индивидуального отношения к риску. Однако в соответствии с заданными допущениями рациональный инвестор всегда будет выбирать портфель, лежащий на эффективной границе. Этот выбор осуществляется посредством анализа и определения приемлемого соотношения риска и доходности для каждого инвестора.
Задача определения оптимального портфеля для конкретного инвестора может быть решена аналитически — минимизацией
риска, выраженного дисперсией или стандартным отклонением при заданном уровне доходности, либо максимизацией доходности при заданном уровне риска. В классической постановке Марковица задача формирования оптимального портфеля имеет вид
Задача (9.14)—(9.16) решается методами квадратичного программирования. Решение этой задачи требует предварительной оценки N доходностей, N дисперсий и (N2 — N) / 2 ковариаций, т. е. (N2 + 3N) / 2 параметров (например, анализ 20 рисковых бумаг потребует оценки 230 параметров). Следует отметить, что в настоящее время в вычислительном отношении провести подобную оценку не составляет большого труда, в частности для этих целей можно использовать специальные средства популярного офисного пакета MS EXCEL.
Подходу Марковица присущи и другие ограничения, связанные с положенными в его основу допущениями. Вместе с тем полученные им результаты положили начало современной теории портфельного инвестирования, дали мощный толчок к дальнейшим исследованиям и в целом сохраняют свою актуальность по нынешний день.
Источник
Asset Allocation: корреляция активов
Автор: Алексей Мартынов · Опубликовано 23.05.2016 · Обновлено 22.08.2016
В предыдущей статье мы говорили, что ребалансировка активов контролирует риск портфеля, а при удачном стечении обстоятельств может дать дополнительный выигрыш по доходности. Но это работает только в том случае, если активы в портфеле ведут себя по разному в одних и тех же условиях. Как найти такие активы, и как оценить их поведение между собой, вы узнаете из этой статьи.
В портфель должны включаться слабо взаимосвязанные активы, цена которых ведет себя по разному в одинаковых условиях. Это снижает риск портфеля и создает портфельный эффект. Связь разных активов между собой можно оценить математически с помощью корреляции. Корреляция показывает в какой степени динамика стоимости одного актива соотносится с динамикой другого актива.
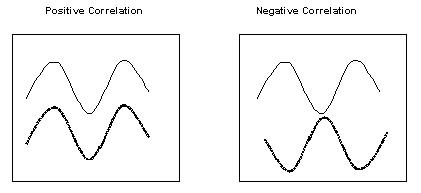
Корреляция может принимать значения от +1 (положительная) до -1 (отрицательная). Если цены активов движутся в одном направлении (оба растут или оба снижаются), корреляция положительна (больше 0), если цены активов движутся в противоположных направлениях (один растет, второй снижается), корреляция отрицательная (меньше 0). 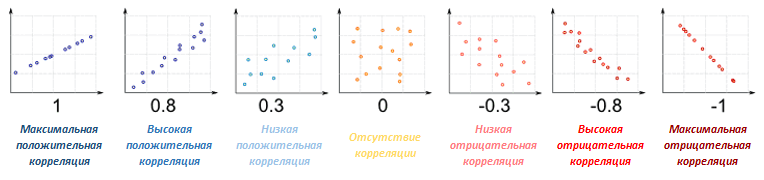
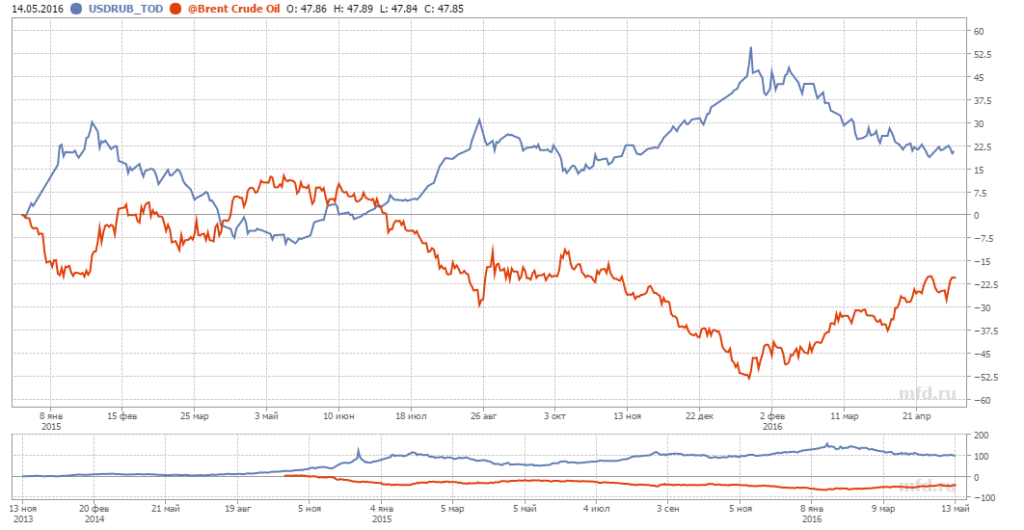
Из реальной жизни пример негативной корреляции можно найти в динамике курса доллара и цен на нефть в 2015-16 годах: когда нефть падала, курс доллара рос.
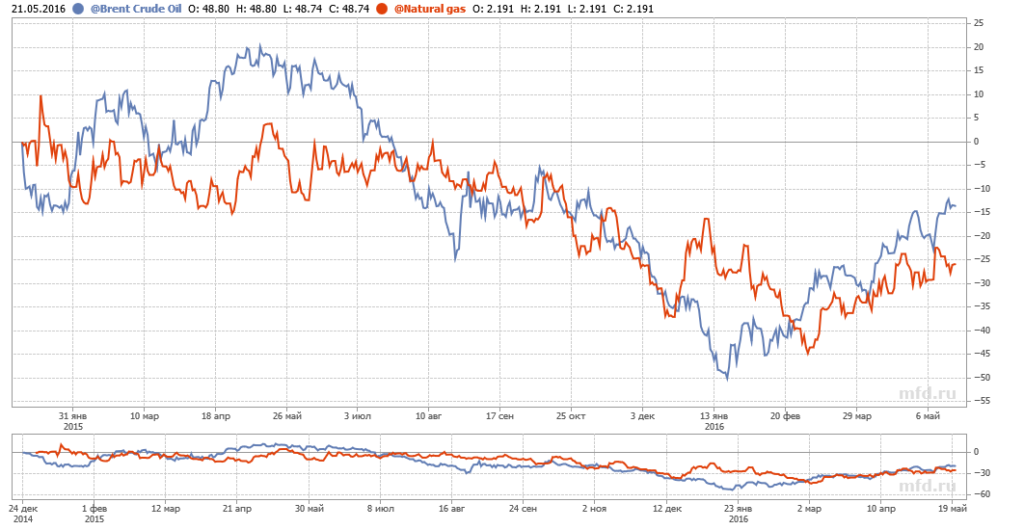
Положительная корреляция есть между ценами на нефть и натуральный газ: их цены двигаются схожим образом.
Влияние корреляции на риск портфеля
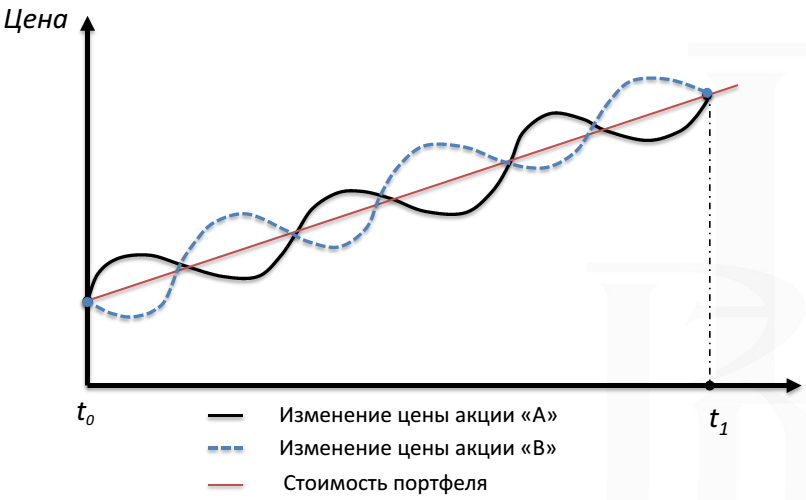
Поведение активов влияет на риск портфеля. Например, на картинке ниже изображены две акции, стоимость которых изменяется противоположно: когда одна растет, другая падает. Корреляция таких акций будет отрицательной. Если портфель будет состоять поровну их этих акций, то его стоимость будет изменяться гораздо плавнее по сравнению с каждой акцией в отдельности, то есть риск портфеля будет ниже, чем риск составляющих его акций. Это конечно идеализированная модель, но она наглядно показывает, как отрицательная корреляция активов снижает риск портфеля.
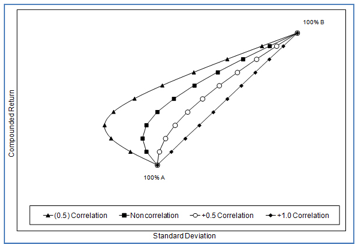
Теперь посмотрим, как корреляция может влиять на риск и доходность портфеля. На графике ниже изображена так называемая граница эффективности портфеля, состоящего из двух активов — А и В. Вертикальная ось — доходность портфеля, горизонтальная ось — стандартное отклонение доходности. Каждая линия представляет собой портфель с разной степенью корреляции активов (-0.5, 0.0, +0.5 и +1.0). Каждая точка на линии — это разные пропорции активов в портфеле, начиная от 100% А, далее 90% А:10% В и так далее до 100% В.
Источник: Richard Ferri, Portfolio Solutions
Нетрудно заметить, что портфели активов с отрицательной корреляцией -0,5 находятся в левой части диаграммы и имеют самое низкое стандартное отклонение доходности, то есть самый низкий риск среди всех рассматриваемых портфелей. А портфели активов с высокой корреляцией имеют самый высокий риск. Таким образом при прочих равных риск портфеля снижается когда активы имеют низкую корреляцию.
Корреляция активов
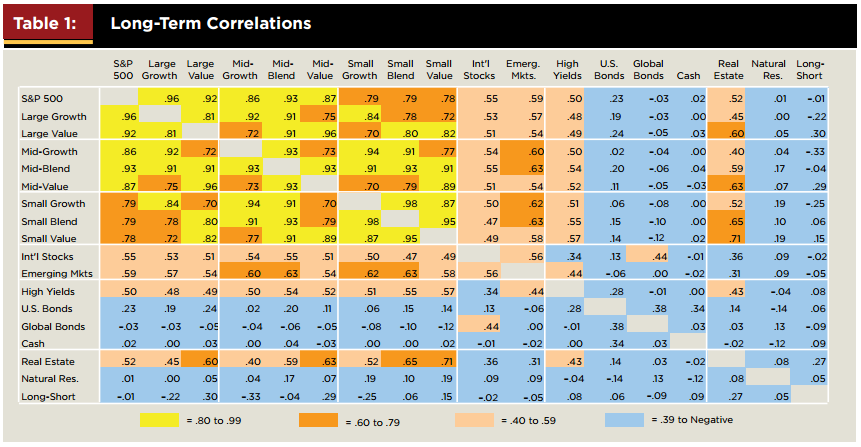
К сожалению, в реальной жизни довольно трудно найти два актива с абсолютно нулевой или отрицательной корреляцией. Большинство активов имеют корреляцию где-то между 0 и+1. В таблице 1 представлена матрица корреляции между разными классами активов с 1970 по 2004 год. Чем холоднее цвет, тем ниже корреляция. Можно заметить, что холодные цвета присутствуют в основном у облигаций, кэша и ресурсов. Эти классы активов хуже всего коррелируют с акциями различной капитализации и недвижимостью. Однако даже среди них редко встречаются отрицательные значения.
Источник: Journal of financial planning
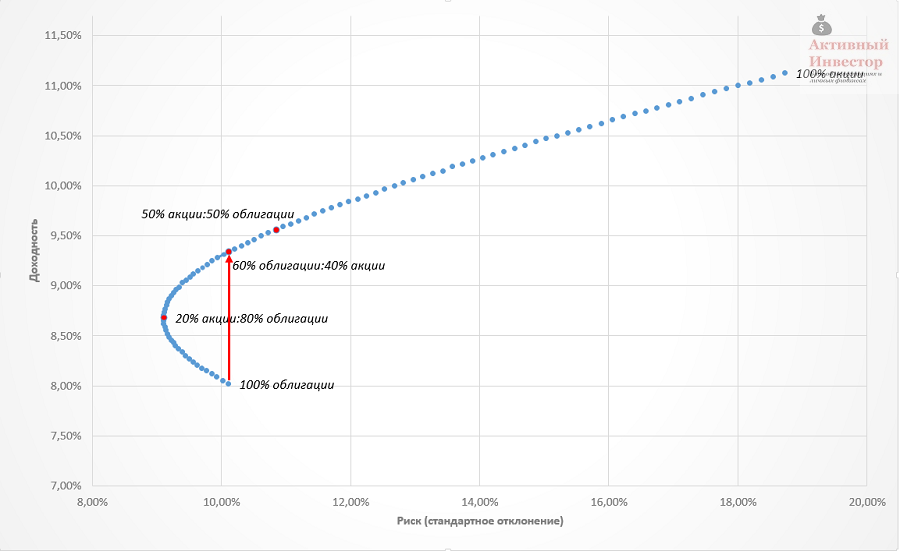
Если взять реальный пример, то корреляция между американскими акциями и долгосрочными государственными облигациями на сроке 1972-2015 составила 0,01, то есть фактически отсутствовала. Граница эффективности портфеля, состоящего их этих двух классов активов очень похожа на линию на графике выше, которая соответствует портфелю из некоррелируемых активов.
Низкая корреляция между активами создает портфельный эффект — когда по характеристикам риск и доходность портфеля может быть лучше активов, из которых он состоит. Логично было бы ожидать, что самый низкий риск будет иметь портфель, состоящий полностью из облигаций. Но в реальности самым низким риском обладает портфель, доля облигаций в котором 80%, а на акции приходится 20%. Добавление акций не только уменьшило риск портфеля, но и увеличило его доходность на 0,6%. Другой портфель 60:40 показал такой же риск, как и 100% облигаций, но его доходность при этом была почти на 1,5% больше.
Корреляция непостоянна
Ричард Ферри в своей статье в журнале Forbes обратил внимание, что, к сожалению, теория, которая красиво выглядит на длительном сроке, не всегда хорошо работает на коротких периодах. Например, с 1926 по 2013 год корреляция между акциями США и 5-летними казначейскими облигациями была равна 0,07. Это очень низкая корреляция для двух классов активов, значит эти два класса активов в портфеле должны хорошо работать вместе.
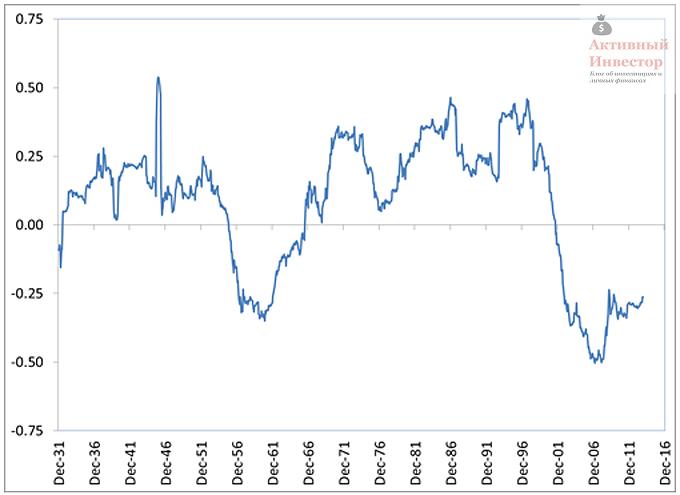
К сожалению, долговременная корреляция не отражает то, что происходит в течение коротких периодов. На графике ниже показано, как сильно может меняться корреляция на коротком сроке. На рисунке изображена 5-ти летняя скользящая корреляция между американскими акциями и 5-летними облигациями, рассчитанная на отрезке 1926-2013.
Источник: Richard Ferri, Portfolio Solutions
Пятилетняя корреляция колебалась в диапазоне от -0,5 до +0,5 и лишь изредка равнялась долгосрочной. Это означает, что какую-то часть времени стоимость активов менялась схожим образом, какую-то часть времени — противоположно. Корреляция активов не статична и меняется со временем, иногда очень сильно. Поэтому реализация преимущества низкой корреляции может потребовать длительного времени величиной с десятилетия.
Теперь возьмем и сравним поведение портфеля на двух временных промежутках: с 1970-1985 и с 2002-2013. В период с 1970-1985 корреляция между этими двумя классами активов составляла около +0,3, что привело к доходности портфеля 50:50 всего на 0,5% больше облигаций.
За период с 2002 по 2013 год корреляция между этими двумя классами активов составила около -0,3, в результате чего доходность портфеля превзошла доходность облигаций на 1,7%. Разная корреляция активов может очень сильно менять результаты одного и того же портфеля.
Источник: Richard Ferri, Portfolio Solutions
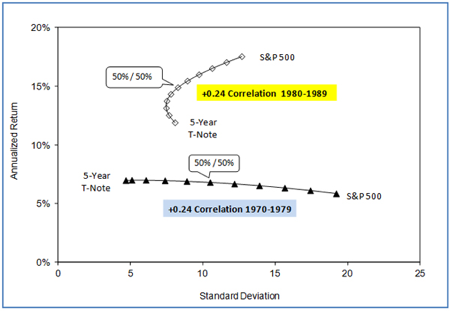
Но даже если корреляция в будущем будет такой же, как она была в прошлом, результаты все равно могут отличаться. Например, 10-летняя корреляция между 5-летними облигациями и акциями США в 70-х годах была +0,24, такой же она была и в 80-х. Но результаты портфелей были различными.
Источник: Richard Ferri, Portfolio Solutions
Низкая корреляция в 70-х годах не дала особых преимуществ: риск портфеля 50/50 оказался выше, а доходность ниже, чем у облигаций. В 80-х аналогичный портфель показал результат гораздо лучше: на 3% больше доходности облигаций при аналогичном риске. Поэтому низкая корреляция двух активов еще не гарантирует уменьшение риска портфеля на коротком сроке.
С течением времени активы с низкой корреляцией находить стало труднее. Финансовые рынки стали более глобальными и взаимосвязанными. Локальный ипотечный кризис 2008 года в США затронул весь мир. Глобализация финансовых рынков сделала так, что инструменты сейчас коррелируют в большей степени, чем раньше. Величина корреляции активов в прошлом зависит от взятого периода и не является надежным индикатором корреляции в будущем.
- Активы, включаемые в портфель, должны иметь низкую положительную или отрицательную корреляцию.
- Низкая корреляция снижает риск портфеля и может увеличить его доходность.
- Долгосрочная корреляция в прошлом — плохой прогнозный индикатор будущей корреляции в краткосрочной перспективе.
- Краткосрочная корреляция — величина непостоянная и может значительно меняться.
- Поэтому для реализации преимущества низкой корреляции требуется длительное время.
- На промежутках времени до 10 лет портфельный эффект может отсутствовать.
Тем не менее это вовсе не означает, что про корреляцию можно совсем забыть. В портфель нужно включать фундаментально разные активы. Высокая положительная корреляция означает отсутствие фундаментальных отличий по риску между активами. Например, высокая положительная корреляция между акциями крупной и средней капитализации будет всегда. Диверсификация по таким активам не принесет большой выгоды портфелю в плане снижения риска. Слабая положительная или отрицательная корреляция служит признаком отличий между активами в плане риска, поэтому включение в портфель активов с низкой положительной или отрицательной корреляцией потенциально уменьшает его риск и создает портфельный эффект, о котором будет написана следующая статья.
Источник