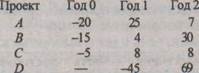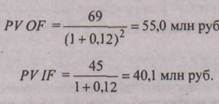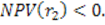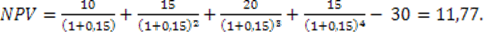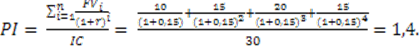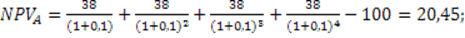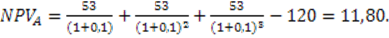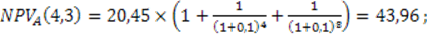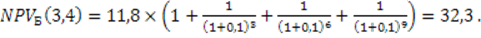Предприятие имеет возможность инвестировать до 60 тыс руб

Решение. Б. Рассматриваемые проекты не поддаются дроблению

Пример

Пример

Б. Рассматриваемые проекты не поддаются дроблению

Пример

Предположим, что компания имеет возможность инвестировать:

а) до 55 млн руб.;

б) до 90 млн руб.,

Стоимость источников финансирования составляет 10%. Требуется составить оптимальный инвестиционный портфель, если имеются следующие альтернативные проекты:

проект D: -15; 4; 5; 6; 6.

Инвестиции осуществляются в нулевой период.

Рассчитаем чистый приведенный эффект (NPV) и индекс рента­бельности для каждого проекта (PI):

проект A: NPV =2,51; PI= 1,084; IRR = 13,4%;

проект В: NPV= 2,68; Р1= 1,134; IRR = 15,6%;

проект С: NPV= 4,82; Р1= 1,121; IRR = 15,3%;

проект D: NPV= 1,37; Р1= 1,091; IRR = 13,9%.

Таким образом, по убыванию показателя PI проекты упорядочива­ются следующим образом :B,C,D,A.

Вариант (а): Наиболее оптимальной будет стратегия:

проект	инвестиции	Часть инвестиций, включаемая в портфель, %	NPV
Всего

Можно проверить, что любая другая комбинация ухудшает резуль­таты — уменьшает суммарный NPV.

Таким образом, действительно была найдена оптимальная страте­гия формирования инвестиционного портфеля.

Вариант (б): Наиболее оптимальной будет стратегия:

проект	инвестиции	Часть инвестиций, включаемая в портфель, %	NPV
Всего

Б. Рассматриваемые проекты не поддаются дроблению

В этом случае оптимальную комбинацию находят перебором в, возможных вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта. Комбинация, максимизирующая суммарный NPV, будет оптимальной.

В условиях предыдущего примера составить оптимальный инвес­тиционный портфель, если верхний предел инвестиций — 55 млн руб., но проекты не поддаются дроблению.

Возможны следующие сочетания проектов в портфеле: А + В, А + D,B + D,C + D. Рассчитаем суммарный NPV для каждого варианта:

Вариант	Суммарная инвестиция	суммарный NPV
А+B
A+D
B+D
C+D

Таким образом, оптимальным является инвестиционный портфель, включающий проекты С и D.

Когда речь идет о временной оптимизации, имеется в виду следу­ющая ситуация:

• общая сумма финансовых ресурсов, доступных для финансиро­вания в планируемом году, ограничена сверху;

• имеется несколько доступных независимых инвестиционных проектов, которые ввиду ограниченности финансовых ресурсов не могут быть реализованы в планируемом году одновременно, однако в следующем за планируемым годом оставшиеся проекты либо их части могут быть реализованы;

• требуется оптимальным образом распределить проекты по двум годам.

В основу методики составления оптимального портфеля в этом случае заложена следующая идея: по каждому проекту рассчитывается специальный индекс, характеризующий относительную потерю NPV в случае, если проект будет отсрочен к исполнению на год. Проекты с минимальными значениями индекса могут быть отложены на следу­ющий год. Очевидно, что ключевую роль в данной методике вновь играет показатель PI.

В условиях примера с проектами, поддаю­щимися дроблению, составить оптимальный инвестиционный порт­фель на два года в случае, если объем инвестиций на планируемый год ограничен суммой в 70 млн руб.

Рассчитаем потери в NPV в случае, если каждый из анализируе­мых проектов будет отсрочен к исполнению на год:

проект	NPV в году1	Дисконтированный множитель при r=10%	NPV в году 0 (гр.2*гр.3)	Потеря в NPV (гр.2-гр.4)	Величина отложенной на год инвестиции	Индекс возможных потерь (гр.5/гр.6)
A	2,51	0,9091
B	2,68	0,9091
C	4,82	0,9091
D	1,37	0,9091

Индекс возможных потерь имеет следующую интерпретацию: он показывает, чему равна величина относительных потерь в случае от­кладывания проекта к исполнению на год. Из расчета видно, что наи­меньшие потери будут в том случае, если отложен к исполнению про­ект А, затем последовательно проекты D, С, В.

Таким образом, инвестиционный портфель года 1 должен вклю­чить проекты В и С в полном объеме, а также часть проекта D; оставшуюся часть проекта D и проект А следует включить в порт­фель года 2:

проект	инвестиция	Часть инвестиции, включаемая в портфель, %	NPV
А) инвестиции в году 0
Всего
Б) инвестиции в году 1
Всего

Суммарный NPV при таком формировании портфелей за два года составит 11,11 млн руб. (8,42 + 2,69), а общие потери — 0,27 млн руб. (2,51 +2,68 + 4,82+ 1,37- 11,11) и будут минимальны по сравнению с другими вариантами формирования портфелей.

ОПТИМИЗАЦИЯ В УСЛОВИЯХ РЕИНВЕСТИРОВАНИЯ ДОХОДОВ

Приведем еще один пример, показывающий, что тра­диционные рекомендации, в частности в отношении критерия PI, не всегда оправданны.

Компания имеет возможность инвестировать ежегодно не более 20 млн руб.; кроме того, все доходы от дополнительно введенных ин­вестиционных проектов также могут использоваться для целей инве­стирования. На момент анализа являются доступными следующие не­зависимые проекты:

Требуется составить портфель капиталовложений, если стоимость источников финансирования 12%.

Прежде чем приступать к составлению портфеля, необходимо рас­считать значения критериев NPV и PI для каждого проекта при сто­имости капитала СС = 12%:

Следует отметить, что критерий Р1 в данном случае рассчитывает­ся соотнесением приведенных стоимостей денежных притоков (IF) и денежных оттоков (OF), причем расчет ведется на конец года 0. В ча­стности, для проекта D:

Таким образом, для проекта D: РI= 1,37.

Значения критерия NPV дают основание сделать вывод, что все проекты являются приемлемыми; критерий PI дает возможность ран­жировать их по степени предпочтительности: С, В, A, D. Что касается составления портфеля капиталовложений, то число вариантов здесь ограничено.

Поскольку объем капиталовложений нулевого года ограничен 20 млн руб., то очевидно, что компания имеет две альтернативы: при­нять проект А или принять комбинацию проектов В и С. С позиции критерия PI комбинация проектов В и С более выгодна, а суммарный NPV в этом случае равен 21 млн руб.

С другой стороны, принятие этой комбинации автоматически де­лает невозможным принятие проекта D, поскольку компания не будет иметь источников средств в достаточном объеме, так как сумма, на которую может рассчитывать компания, равна 32 млн руб. (20 млн руб. из запланированных источников и 12 млн руб. генерируемых проек­тами В и С). Если же будет принят проект А, то к концу первого года у компании появятся средства и для принятия проекта D: 20 млн руб. из запланированных источников плюс 25 млн руб., генерируемых про­ектом А. Иными словами, речь идет о выборе между комбинацией (В + С), с одной стороны, и комбинацией (А + D), с другой стороны. По­скольку вторая комбинация обеспечивает большее значение совокуп­ного NPV (7,9 + 14,8 = 22,7 млн руб.), то она, безусловно, является более предпочтительной.

Таким образом, критерий PI в данном случае не срабатывает, и вновь приходится прибегать к критерию NPV.

Более сложные ситуации, аналогичные только что описанной, ре­шаются с помощью методов оптимального программирования.

Задача 1. Компания имеет возможность инвестировать 1000 тыс. руб. Инвестиции осуществляются в 0 –ой год Стоимость источников финансирования составляет 8%. Имеются следующие альтернативные проекты:

Проект D: -300; 70; 85; 120; 130.

Проект E:-150; 20; 40; 60; 80

Требуется составить оптимальный инвестиционный портфель, если:

Источник

Тема 3. Анализ капитальных вложений

В практике финансового анализа и выбора целесообразного варианта инвестиций используются показатели двух категорий:

— учетные показатели (без влияния фактора времени);

— дисконтированные показатели (например, чистый приведенный доход, рентабельность, внутренняя норма доходности).

Ниже представлены наиболее часто используемые показатели.

Чистый приведенный доход (NPV) – это разница между суммой дисконтированных денежных поступлений, генерируемых по проекту, и суммой затрат, связанных с реализацией проекта

(3.1)

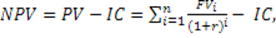
где IC – первоначальные инвестиции;

PV – текущая стоимость будущих денежных поступлений;

FV_i – поступления денежных средств в конце i-го периода;

r – процентная ставка (норма прибыли).

Если денежный поток проекта неординарный, то формула для расчета чистой текущей стоимости будет иметь следующий вид:

, (3.2)

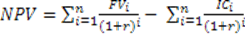
где 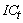– инвестиционные затраты в i-й период.

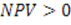
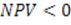
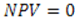
Логика использования показателя для принятия решений очевидна. Если , то проект следует принять, если – отвергнуть, если, то проект ни прибыльный, ни убыточный.

Показатель NPV аддитивен, т.е. NPV различных проектов можно суммировать, что позволяет использовать критерий в качестве основного при анализе оптимальности инвестиционного портфеля.

Индекс рентабельности инвестиций (PI) – это относительный показатель, характеризующий уровень доходов на единицу затрат

. (3.3)

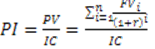
Очевидно, что если PI > 1, то проект следует принять (при условии, что другие критерии также характеризуют его приемлемость); если PI 0, то PI > 1).

Внутренняя норма доходности (IRR) – это такое значение коэффициента дисконтирования, при котором чистый приведенный эффект равен нулю.

(3.4)

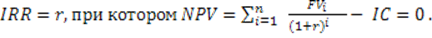
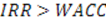
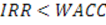
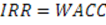
В целях анализа целесообразности инвестирования внутреннюю норму доходности сопоставляют с ценой авансированного капитала (WACC), которая отражает минимум возврата на вложенный капитал (см. тему 8). Очевидно, что если – проект следует принять, – проект отвергается, при требуется дополнительный анализ.

Поскольку, NPV = f(r), то очевидно, что для интервала (r₁;r₂), в котором функция меняет свой знак с “+” на “-”, можно рассчитать значение IRR по следующей формуле:

(3.5)

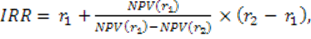
где r₁ – ставка дисконтирования, при которой ;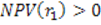

r₂ – ставка дисконтирования, при которой

Срок окупаемости (РР) является одним из распространенных показателей и не предполагает временной упорядоченности денежных поступлений. Алгоритм расчета срока окупаемости зависит от равномерности распределения доходов от инвестиции. Если доход распределен по годам равномерно, то срок окупаемости равен

(3.6)

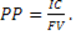
Если прибыль распределена неравномерно, то срок окупаемости определяется прямым подсчетом числа лет, в течение которых инвестиции будут погашены кумулятивным доходом. Общая формула расчета PP:

PP = n, при котором 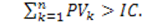(3.7)

При учете временного аспекта в расчете PP используются денежные потоки, дисконтированные по цене авансированного капитала. При этом срок окупаемости увеличивается.

Коэффициент эффективности инвестиции (ARR) рассчитывается делением среднегодовой прибыли (PN) на среднюю величину инвестиции (если по истечении срока капитальные затраты будут списаны). Если допускается наличие остаточной или ликвидационной стоимости (RV), то ее оценка должна быть учтена.

(3.8)

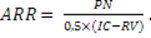
При принятии решений по альтернативным проектам вводится понятие точки Фишера, которая соответствует значению коэффициента дисконтирования, при котором проекты имеют одинаковый уровень NPV.

Часто на практике требуется принятие решения по альтернативным проектам различной продолжительности. В этом случае рекомендуется:

— найти наименьшее общее кратное сроков z = НОК (i,j);

— рассматривая каждый из проектов как повторяющийся, определить NPV проектов, реализуемых необходимое число раз в течение периода z;

— выбрать тот проект из исходных, для которого суммарный NPV повторяющегося потока имеет наибольшее значение.

Суммарный NPV повторяющегося потока равен

(3.9)

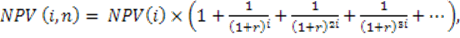
где NPV (i) – чистый приведенный эффект исходного проекта;

i – продолжительность проекта;

r – коэффициент дисконтирования в долях единицы;

n – число повторений проекта.

Методику сравнения проектов различной продолжительности можно упростить в вычислительном плане, предположив, что каждый из анализируемых проектов может быть реализован неограниченное число раз. В этом случае число слагаемых в формуле расчета NPV будет стремиться к бесконечности и формула примет следующий вид:

(3.10)

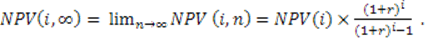
Значение NPV, полученное по формуле (3.10), не соответствует реальному уровню показателя по проекту, тем не менее оно может быть использовано при решении вопросов выбора проекта. Из сравниваемых проектов является предпочтительным проект, имеющий большее значение NPV (i, ∞).

При оценке эффективности капитальных вложений необходимо учитывать влияние инфляции. Общая формула, связывающая обычный коэффициент дисконтирования (r), применяемый в условиях инфляции, номинальный коэффициент дисконтирования (p) и индекс инфляции (i):

. (3.11)

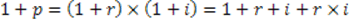
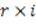
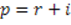
Величиной ввиду ее малости в практических расчетах пренебрегают, поэтому окончательная формула имеет вид

, (3.12)

где r – коэффициент дисконтирования;

p – номинальный коэффициент дисконтирования;

i – индекс инфляции.

3.2. Методические рекомендации

Задача 1. На строительство цеха израсходовано 30 млн руб. Денежные поступления составят: 1-й год – 10 млн руб., 2 год – 15 млн руб., 3 год – 20 млн руб., 4 год – 15 млн руб. Ставка дисконтирования равна 15 %. Определите целесообразность строительства цеха на основании показателей NPV и PI.

1. Рассчитаем NPV по проекту (млн руб.) по (3.1):

2. Определим PI по формуле (3.3):

Инвестирование целесообразно, так как NPV > 0, PI > 1.

Задача 2. Используя следующие данные, сделайте выбор в пользу той или иной модели при ставке процента 10 %:

1) Модель А: цена – 100 тыс. руб., генерируемый годовой доход – 38 тыс. руб., срок эксплуатации – 4 года.

2) Модель Б: цена – 120 тыс. руб., генерируемый годовой доход – 53 тыс. руб., срок эксплуатации – 3 года.

Приведем проекты в сопоставимый вид по сроку эксплуатации.

1. НОК сроков эксплуатации моделей: z = НОК (3,4) = 12.

2. Найдем NPV (тыс. руб.) для исходных проектов по (3.1):

Рассмотрим каждый из проектов как повторяющийся (тыс. руб.). В течение анализируемого срока проект А повторяется 3 раза, а проект Б – 4 раза.

3. На основании расчетных значений NPV предпочтительнее модель А.

3.3. Задачи для самостоятельной работы

Задача 1. Анализируются два проекта по 10 млн руб. каждый. Проекты рассчитаны на 2 года. Денежные поступления от реализации проекта А составляют 10 млн руб. во втором году. По проекту В планируется поступление 14,4 млн руб. в первом году и 2,4 млн руб. во втором году. Рассчитать NPV при ставке 10 % годовых.

Задача 2. Анализируются следующие проекты (руб.):

Ранжируйте проекты по критериям IRR, PP, NPV. Коэффициент дисконтирования равен 10 %. Введите точку Фишера.

Задача 3. Рассматриваются два альтернативных проекта. Первоначальные инвестиции: по проекту А – 43 тыс. руб., по проекту В – 78 тыс. руб. Срок реализации проектов – 5 лет. Ожидаемые денежные поступления: по проекту А – по 16 тыс. руб. ежегодно в течение 5 лет, по проекту В – 141 тыс. руб. в год окончания проекта. Введите точку Фишера. Какой проект предпочтительнее при коэффициенте дисконтирования: а) 5 %, б) 10 %?

Задача 4. На основе данных определите чистый приведенный доход и индекс рентабельности при ставке дисконтирования 13 %.

Затраты, тыс. руб.

Задача 5. Предприятие инвестировало в строительство отеля 40 млн руб. Ежегодные планируемые поступления от эксплуатации отеля в течение четырех лет составят: 15, 20, 24 и 37 млн руб. соответственно. Ставка дисконтирования планируется на уровне 10 %. Определить период окупаемости инвестиций с учетом дисконтированных потоков и номинальных денежных потоков.

Задача 6. Рассчитайте IRR проекта, сроком 3 года, требующего инвестиций в размере 10 млн руб. Денежные поступления составят: 1 год – 3 млн руб., 2 год – 4 млн руб., 3 год – 7 млн руб.

Задача 7. Оцените целесообразность принятия проекта по методу чистого приведенного дохода, если первоначальные затраты на проект составляют 3,5 млн руб., срок реализации проекта – 3 года, ежегодные амортизационные отчисления по проекту составляют 1,5 млн руб., средневзвешенная цена капитала с учетом риска – 45 %. Поступления и затраты по годам представлены в таблице:

Поступления, млн руб.

Затраты, млн руб.

Задача 8. Рассматриваются 2 альтернативных варианта повышения эффективности производства: 1 – приобретение оборудования со сроком эксплуатации 3 года; 2 – покупка производственной системы со сроком эксплуатации 6 лет.

Показатели, млн руб.

Первоначальные инвестиции по проектам

Экономия текущих затрат в год

Обоснуйте принимаемое решение при ставке процента 10 %.

Задача 9. Предприятие предполагает заменить часть оборудования в целях повышения его производительности. При инвестиционном проекте “А” в течение 6 лет (срок работы нового оборудования) предполагается следующее поступление чистых денежных средств (текущие доходы минус текущие расходы плюс амортизация) (в тыс. руб.): 1-й год – 100, 2-й год – 200, 3-й год – 300, 4-й год – 300, 5-й год – 400, 6-й год – 500. Первоначальные вложения, включающие стоимость покупки и установки нового оборудования, составляют 900 тыс. руб. Кроме того, в 3-м году предполагается провести переналадку нового оборудования, стоимость которой составит 200 тыс. руб.

Альтернативным вариантом для инвестиционного проекта «А» является инвестиционный проект «Б», предусматривающий покупку и установку более дорогого оборудования стоимостью 1 200 тыс. руб., которое может проработать все 6 лет без переналадки. При этом предполагается следующее поступление чистых денежных средств (в тыс. руб.): 1-й год – 500, 2-й год – 400, 3-й год – 300, 4-й год – 300, 5-й год – 200, 6-й год – 100. Определить все возможные расчетные показатели инвестиционного проекта «Б» и сравнить их с аналогичными показателями инвестиционного проекта «А». Выбрать наиболее выгодный вариант при ставке процента 10 %.

Задача 10. Компания реализует проект, требующий ежегодные вложения по 100 млн руб. в течение 3-х лет. В начале четвертого года новый объект можно будет использовать. Это обеспечит получение чистого дохода 100 млн руб. ежегодно на протяжении 5 лет. Ставка дисконтирования 10 %. Рассчитать чистую приведенную стоимость проекта на момент сдачи нового объекта в эксплуатацию.

Задача 11. Предприятие планирует закупить линию по производству деталей стоимостью 1 млн руб. и сроком эксплуатации 10 лет. Это обеспечит дополнительную ежегодную прибыль в размере 200 тыс. руб. (без вычета налогов и процентов за кредит). Ставка налогообложения 24 %. За 10 лет стоимость линии будет полностью списана. Рассчитать рентабельность инвестиций и среднюю норму прибыли на инвестиции.

Задача 12. Определить чистую приведенную стоимость и внутреннюю норму доходности инвестиционного проекта и сделать вывод о целесообразности реализации проекта на основании следующих данных: первоначальные инвестиции – 8 млн руб., срок проекта – 4 года, ежегодные амортизационные отчисления – 2 млн руб., ставка налога на прибыль – 24 %, средневзвешенная стоимость капитала, включающая инфляционную премию – 25 %. Поступления и затраты в ценах базового года представлены в таблице (млн руб.):

Источник