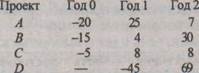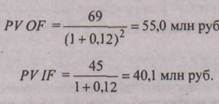Пример 3. Компания имеет возможность инвестировать до 55 млн
Пример 2.
Компания имеет возможность инвестировать до 55 млн. руб., при этом цена источников финансирования составляет 10%. Требуется составить оптимальный инвестиционный портфель, если имеются следующие альтернативные проекты:
проект А: -30; 6; 11; 13; 12
проект В: -20; 4; 8; 12; 5
проект С: -40; 12; 15; 15; 15
проект D: -15; 4; 5; 6; 6
Рассчитаем чистый дисконтированный доход (NPV) и индекс рентабельности инвестиций (PI) для каждого проекта
проект A: NPV = 2,51; PI = 1,084; IRR = 13,4%
проект В: NPV = 2,68; PI = 1,134; IRR = 15,6%
проект С: NPV = 4,82; PI = 1,121; IRR = 15,3%
проект D: NPV = 1,37; PI = 1,091; IRR = 13,9%
Таким образом, по убыванию показателя PI проекты упорядочиваются следующим образом: В, С, D, А.
Наиболее оптимальной будет стратегия:
| Проект | Инвестиция, млн. руб. | Часть инвестиции, включаемая в портфель, % | NPV |
| В | 2,68 | ||
| С | 87,5 | 4,22 | |
| Итого | 6,9 |
Можно проверить, что любая другая комбинация ухудшает результаты – уменьшает суммарный NPV. В частности, проверим вариант, когда проект С, как имеющий наивысший NPV, в полном объеме включается в инвестиционный проект:
| Проект | Инвестиция, млн. руб. | Часть инвестиции, включаемая в портфель, % | NPV |
| С | 4,82 | ||
| В | 2,01 | ||
| Итого | 6,83 |
Таким образом, действительно была найдена оптимальная стратегия формирования инвестиционного портфеля.
Б. Рассматриваемые проекты не поддаются дроблению
В этом случае оптимальную комбинацию находят перебором всех возможных вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта. Комбинация, максимизирующая суммарный NPV, будет оптимальной.
В условиях предыдущего примера составить оптимальный инвестиционный портфель, если верхний предел инвестиций составляет 55 млн. руб., но проекты не поддаются дроблению.
Возможны следующие сочетания проектов в портфеле: А+В, A+D, B+D, C+D. Рассчитаем суммарный NPV для каждого варианта:
| Вариант | Суммарная инвестиция, млн. руб. | Суммарный NPV |
| А + В | 50 (30 + 20) | 5,19 (2,51 + 2,68) |
| A + D | 45 (30 + 15) | 3,88 (2,51 + 1,37) |
| В + D | 35 (20 + 15) | 4,05 (2,68 + 1,37) |
| C + D | 55 (40 + 15) | 6,19 (4,82 + 1,37) |
Таким образом, оптимальным является инвестиционный портфель, включающий проекты С и D.
2. Временная оптимизация
Временная оптимизация состоит в следующем:
§ общая сумма финансовых ресурсов, доступных для финансирования в планируемом году, ограничена сверху;
§ имеется несколько независимых инвестиционных проектов, которые ввиду ограниченности финансовых ресурсов не могут быть реализованы в планируемом году одновременно, однако в следующем за планируемым годом оставшиеся проекты либо их части могут быть реализованы;
§ требуется оптимально распределить проекты по двум годам.
Методика составления оптимального портфеля: по каждому проекту рассчитывается специальный индекс возможных потерь, характеризующий относительную потерю NPV, в случае если проект будет отсрочен к исполнению на год. Проекты с минимальными значениями индекса могут быть отложены на следующий год.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Решение. Б. Рассматриваемые проекты не поддаются дроблению
Пример
Пример
Б. Рассматриваемые проекты не поддаются дроблению
Пример
Предположим, что компания имеет возможность инвестировать:
а) до 55 млн руб.;
б) до 90 млн руб.,
Стоимость источников финансирования составляет 10%. Требуется составить оптимальный инвестиционный портфель, если имеются следующие альтернативные проекты:
проект D: -15; 4; 5; 6; 6.
Инвестиции осуществляются в нулевой период.
Рассчитаем чистый приведенный эффект (NPV) и индекс рентабельности для каждого проекта (PI):
проект A: NPV =2,51; PI= 1,084; IRR = 13,4%;
проект В: NPV= 2,68; Р1= 1,134; IRR = 15,6%;
проект С: NPV= 4,82; Р1= 1,121; IRR = 15,3%;
проект D: NPV= 1,37; Р1= 1,091; IRR = 13,9%.
Таким образом, по убыванию показателя PI проекты упорядочиваются следующим образом :B,C,D,A.
Вариант (а): Наиболее оптимальной будет стратегия:
| проект | инвестиции | Часть инвестиций, включаемая в портфель, % | NPV |
| Всего |
Можно проверить, что любая другая комбинация ухудшает результаты — уменьшает суммарный NPV.
Таким образом, действительно была найдена оптимальная стратегия формирования инвестиционного портфеля.
Вариант (б): Наиболее оптимальной будет стратегия:
| проект | инвестиции | Часть инвестиций, включаемая в портфель, % | NPV |
| Всего |
Б. Рассматриваемые проекты не поддаются дроблению
В этом случае оптимальную комбинацию находят перебором в, возможных вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта. Комбинация, максимизирующая суммарный NPV, будет оптимальной.
В условиях предыдущего примера составить оптимальный инвестиционный портфель, если верхний предел инвестиций — 55 млн руб., но проекты не поддаются дроблению.
Возможны следующие сочетания проектов в портфеле: А + В, А + D,B + D,C + D. Рассчитаем суммарный NPV для каждого варианта:
| Вариант | Суммарная инвестиция | суммарный NPV |
| А+B | ||
| A+D | ||
| B+D | ||
| C+D |
Таким образом, оптимальным является инвестиционный портфель, включающий проекты С и D.
Когда речь идет о временной оптимизации, имеется в виду следующая ситуация:
• общая сумма финансовых ресурсов, доступных для финансирования в планируемом году, ограничена сверху;
• имеется несколько доступных независимых инвестиционных проектов, которые ввиду ограниченности финансовых ресурсов не могут быть реализованы в планируемом году одновременно, однако в следующем за планируемым годом оставшиеся проекты либо их части могут быть реализованы;
• требуется оптимальным образом распределить проекты по двум годам.
В основу методики составления оптимального портфеля в этом случае заложена следующая идея: по каждому проекту рассчитывается специальный индекс, характеризующий относительную потерю NPV в случае, если проект будет отсрочен к исполнению на год. Проекты с минимальными значениями индекса могут быть отложены на следующий год. Очевидно, что ключевую роль в данной методике вновь играет показатель PI.
В условиях примера с проектами, поддающимися дроблению, составить оптимальный инвестиционный портфель на два года в случае, если объем инвестиций на планируемый год ограничен суммой в 70 млн руб.
Рассчитаем потери в NPV в случае, если каждый из анализируемых проектов будет отсрочен к исполнению на год:
| проект | NPV в году1 | Дисконтированный множитель при r=10% | NPV в году 0 (гр.2*гр.3) | Потеря в NPV (гр.2-гр.4) | Величина отложенной на год инвестиции | Индекс возможных потерь (гр.5/гр.6) |
| A | 2,51 | 0,9091 | ||||
| B | 2,68 | 0,9091 | ||||
| C | 4,82 | 0,9091 | ||||
| D | 1,37 | 0,9091 |
Индекс возможных потерь имеет следующую интерпретацию: он показывает, чему равна величина относительных потерь в случае откладывания проекта к исполнению на год. Из расчета видно, что наименьшие потери будут в том случае, если отложен к исполнению проект А, затем последовательно проекты D, С, В.
Таким образом, инвестиционный портфель года 1 должен включить проекты В и С в полном объеме, а также часть проекта D; оставшуюся часть проекта D и проект А следует включить в портфель года 2:
| проект | инвестиция | Часть инвестиции, включаемая в портфель, % | NPV |
| А) инвестиции в году 0 | |||
| Всего | |||
| Б) инвестиции в году 1 | |||
| Всего |
Суммарный NPV при таком формировании портфелей за два года составит 11,11 млн руб. (8,42 + 2,69), а общие потери — 0,27 млн руб. (2,51 +2,68 + 4,82+ 1,37- 11,11) и будут минимальны по сравнению с другими вариантами формирования портфелей.
ОПТИМИЗАЦИЯ В УСЛОВИЯХ РЕИНВЕСТИРОВАНИЯ ДОХОДОВ
Приведем еще один пример, показывающий, что традиционные рекомендации, в частности в отношении критерия PI, не всегда оправданны.
Компания имеет возможность инвестировать ежегодно не более 20 млн руб.; кроме того, все доходы от дополнительно введенных инвестиционных проектов также могут использоваться для целей инвестирования. На момент анализа являются доступными следующие независимые проекты:

Требуется составить портфель капиталовложений, если стоимость источников финансирования 12%.
Прежде чем приступать к составлению портфеля, необходимо рассчитать значения критериев NPV и PI для каждого проекта при стоимости капитала СС = 12%:
Следует отметить, что критерий Р1 в данном случае рассчитывается соотнесением приведенных стоимостей денежных притоков (IF) и денежных оттоков (OF), причем расчет ведется на конец года 0. В частности, для проекта D:
Таким образом, для проекта D: РI= 1,37.
Значения критерия NPV дают основание сделать вывод, что все проекты являются приемлемыми; критерий PI дает возможность ранжировать их по степени предпочтительности: С, В, A, D. Что касается составления портфеля капиталовложений, то число вариантов здесь ограничено.
Поскольку объем капиталовложений нулевого года ограничен 20 млн руб., то очевидно, что компания имеет две альтернативы: принять проект А или принять комбинацию проектов В и С. С позиции критерия PI комбинация проектов В и С более выгодна, а суммарный NPV в этом случае равен 21 млн руб.
С другой стороны, принятие этой комбинации автоматически делает невозможным принятие проекта D, поскольку компания не будет иметь источников средств в достаточном объеме, так как сумма, на которую может рассчитывать компания, равна 32 млн руб. (20 млн руб. из запланированных источников и 12 млн руб. генерируемых проектами В и С). Если же будет принят проект А, то к концу первого года у компании появятся средства и для принятия проекта D: 20 млн руб. из запланированных источников плюс 25 млн руб., генерируемых проектом А. Иными словами, речь идет о выборе между комбинацией (В + С), с одной стороны, и комбинацией (А + D), с другой стороны. Поскольку вторая комбинация обеспечивает большее значение совокупного NPV (7,9 + 14,8 = 22,7 млн руб.), то она, безусловно, является более предпочтительной.
Таким образом, критерий PI в данном случае не срабатывает, и вновь приходится прибегать к критерию NPV.
Более сложные ситуации, аналогичные только что описанной, решаются с помощью методов оптимального программирования.
Задача 1. Компания имеет возможность инвестировать 1000 тыс. руб. Инвестиции осуществляются в 0 –ой год Стоимость источников финансирования составляет 8%. Имеются следующие альтернативные проекты:
Проект D: -300; 70; 85; 120; 130.
Проект E:-150; 20; 40; 60; 80
Требуется составить оптимальный инвестиционный портфель, если:
Источник
Пример 3.. Компания имеет возможность инвестировать до 55 млн



Пример 2.
Компания имеет возможность инвестировать до 55 млн. руб., при этом цена источников финансирования составляет 10%. Требуется составить оптимальный инвестиционный портфель, если имеются следующие альтернативные проекты:
проект А: -30; 6; 11; 13; 12
проект В: -20; 4; 8; 12; 5
проект С: -40; 12; 15; 15; 15
проект D: -15; 4; 5; 6; 6
Рассчитаем чистый дисконтированный доход (NPV) и индекс рентабельности инвестиций (PI) для каждого проекта
проект A: NPV = 2,51; PI = 1,084; IRR = 13,4%
проект В: NPV = 2,68; PI = 1,134; IRR = 15,6%
проект С: NPV = 4,82; PI = 1,121; IRR = 15,3%
проект D: NPV = 1,37; PI = 1,091; IRR = 13,9%
Таким образом, по убыванию показателя PI проекты упорядочиваются следующим образом: В, С, D, А.
Наиболее оптимальной будет стратегия:
| Проект | Инвестиция, млн. руб. | Часть инвестиции, включаемая в портфель, % | NPV |
| В | 2,68 | ||
| С | 87,5 | 4,22 | |
| Итого | 6,9 |
Можно проверить, что любая другая комбинация ухудшает результаты – уменьшает суммарный NPV. В частности, проверим вариант, когда проект С, как имеющий наивысший NPV, в полном объеме включается в инвестиционный проект:
| Проект | Инвестиция, млн. руб. | Часть инвестиции, включаемая в портфель, % | NPV |
| С | 4,82 | ||
| В | 2,01 | ||
| Итого | 6,83 |
Таким образом, действительно была найдена оптимальная стратегия формирования инвестиционного портфеля.
Б. Рассматриваемые проекты не поддаются дроблению
В этом случае оптимальную комбинацию находят перебором всех возможных вариантов сочетания проектов и расчетом суммарного NPV для каждого варианта. Комбинация, максимизирующая суммарный NPV, будет оптимальной.
В условиях предыдущего примера составить оптимальный инвестиционный портфель, если верхний предел инвестиций составляет 55 млн. руб., но проекты не поддаются дроблению.
Возможны следующие сочетания проектов в портфеле: А+В, A+D, B+D, C+D. Рассчитаем суммарный NPV для каждого варианта:
| Вариант | Суммарная инвестиция, млн. руб. | Суммарный NPV |
| А + В | 50 (30 + 20) | 5,19 (2,51 + 2,68) |
| A + D | 45 (30 + 15) | 3,88 (2,51 + 1,37) |
| В + D | 35 (20 + 15) | 4,05 (2,68 + 1,37) |
| C + D | 55 (40 + 15) | 6,19 (4,82 + 1,37) |
Таким образом, оптимальным является инвестиционный портфель, включающий проекты С и D.
2. Временная оптимизация
Временная оптимизация состоит в следующем:
§ общая сумма финансовых ресурсов, доступных для финансирования в планируемом году, ограничена сверху;
§ имеется несколько независимых инвестиционных проектов, которые ввиду ограниченности финансовых ресурсов не могут быть реализованы в планируемом году одновременно, однако в следующем за планируемым годом оставшиеся проекты либо их части могут быть реализованы;
§ требуется оптимально распределить проекты по двум годам.
Методика составления оптимального портфеля: по каждому проекту рассчитывается специальный индекс возможных потерь, характеризующий относительную потерю NPV, в случае если проект будет отсрочен к исполнению на год. Проекты с минимальными значениями индекса могут быть отложены на следующий год.
Источник