Построить кривую рыночной доходности

Кривая доходности облигаций и ОФЗ

Кривая доходности облигаций — это отображение на графике процента доходности долговых бумаг, в зависимости от их срока до погашения. Обычно идет сравнение облигаций одного эмитента (например, госбумаг) или нескольких, но принадлежащих к одному сектору (финансовые, нефтяные, металлургия).

Если простыми словами, то инвестор может глядя на график оценить привлекательность (доходность) тех или иных бумаг и выбрать более выгодные для покупки.

Кривая доходности облигаций в классическом варианте может иметь два вида:

• нормальная или классическая;
• перевернутая.

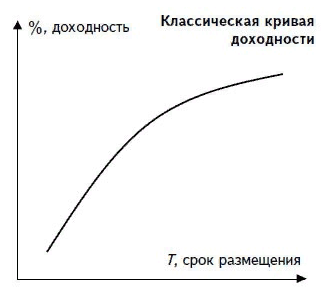
Нормальная кривая доходности

Чем больше срок обращения облигаций, тем более высокую доходность они имеют. Это связано с тем, что инвесторы, покупая длинные бумаги (5-10 лет и выше) несут более высокие риски, перед держателями коротких (1-3 года) бумаг. Повышенные риски связаны с неопределенностью в будущем. За это идет премия за риск, в виде чуть большей доходности.

График характерен для здоровой экономики. Когда участники ожидают дальнего ускорения экономического развития и роста процентных ставок в будущем.

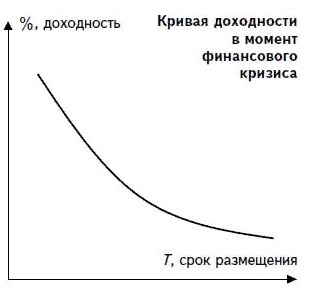
Перевернутая кривая доходности

Обычно такую картину можно наблюдать в момент финансовых кризисов и (или) ожиданием снижения процентных ставок. В это время наблюдается спрос именно на «короткие» деньги.

При такой ситуации можно закупиться длинными бумагами и зафиксировать текущую доходность на долгие годы.

Высокая доходность на короткие облигации — это временное явления. И по истечении срока их жизни, при падении процентной ставки, уже не удастся инвестировать деньги под тот же процент. А вот владельцы длинных бумаг, теряя в доходности в первые года владения, в долгосрочной перспективе выигрывают.

Небольшой пример из реальности. Доходность облигаций напрямую зависит от ставки ЦБ. Как и вклады в банках. Если ЦБ повышает ставку, то эмитенты будут вынуждены при выпуске новых облигаций давать тоже большую доходность. Доходность уже обращающихся бумаг на рынке, после изменения процентной ставки ЦБ будет корректироваться. Чтобы соответствовать среднему значению на бирже.

За счет чего может меняться доходность уже выпущенных бумаг? За счет изменения рыночной стоимости.

• при повышении ставки ЦБ рыночная стоимость облигаций снижается;
• при уменьшение процентной ставки — рыночная цена облигаций повышается.

Когда во время кризиса ЦБ поднимал процентную ставку в 1,5 раза до 18%, новые облигационные выпуски ориентируясь на нее вынуждены были устанавливать аналогичную доходность. И на бирже размещались бумаги с доходностью в 15-20% годовых. С течением времени, каждый новый выпуск давал более высокую ставку по купону.

Старые выпуски, с низкой процентной ставкой по идее уже не кому не нужны. Зачем покупать бумаги с доходностью в 10% годовых, когда есть облигации того же эмитента, но дающие в 1,5 раза больше прибыли.

Чтобы сравниться с текущей доходностью рыночная цена старых бумаг начинается снижаться. И пока ставка ЦБ росла, цена на облигации падали.

После некой стабилизации, ЦБ стал (и продолжает) планомерно снижать процентную ставку. И что мы имеем на рынке?

Новые бумаги выпускаются каждый раз с меньшей доходностью. А старые выпуски постепенно дорожают.

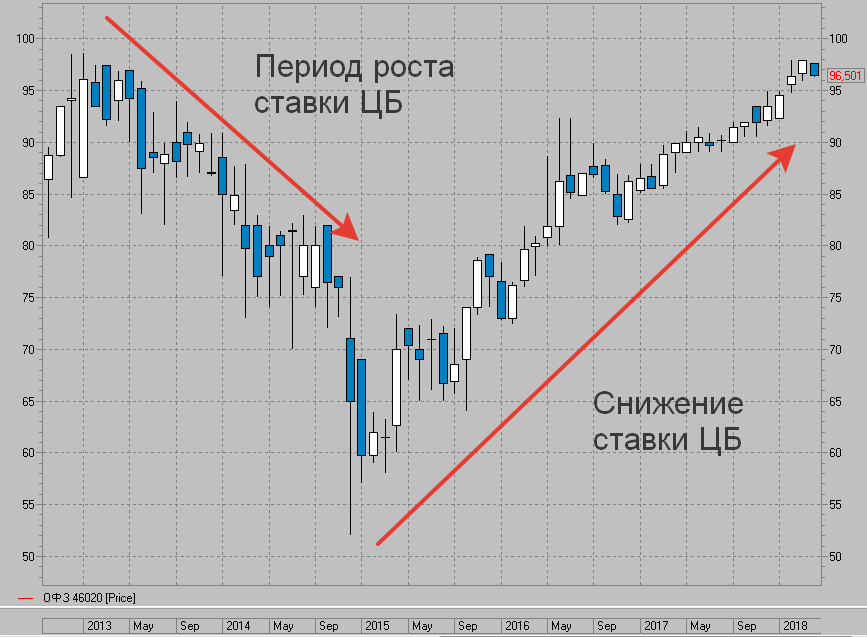
На примере государственных облигаций. За время повышения процентной ставки ЦБ, котировки бумаги снизились почти в 2 раза. И хотя владельцы и получали фиксированные выплаты по купону (7% от номинала в 1 000 рублей), по сравнению с новыми выпусками доходность была намного меньше.

При начале снижения процентной ставки ЦБ, начинается постепенное удорожание бумаг. Купон, выплачиваем владельцам бумаг, начинает приближаться к среднерыночному. И рыночная цена практически достигла докризисных значений.

Если будет и дальше снижение ставки ЦБ, то мы будем наблюдать дальнейшее повышение рыночной стоимости ОФЗ.

Где можно посмотреть кривую доходности?

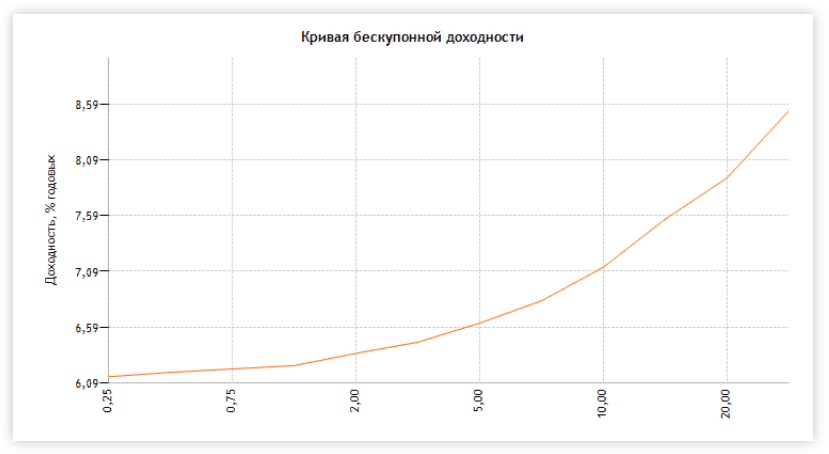
На сайте Центробанка или по ссылке представлен график бескупонной доходности по государственным облигациям или ОФЗ.

И числовые значения кривой зависимости доходности от срока до погашения.

Минус в том, что по этому графику нельзя посмотреть, какие конкретно бумаги дают доходность.

На сайте Cbonds (может потребоваться регистрации) можно посмотреть кривую доходности облигаций различных стран и секторов экономики.

И на графике проанализировать и найти конкретные бумаги с нужной доходностью и сроком до погашения.

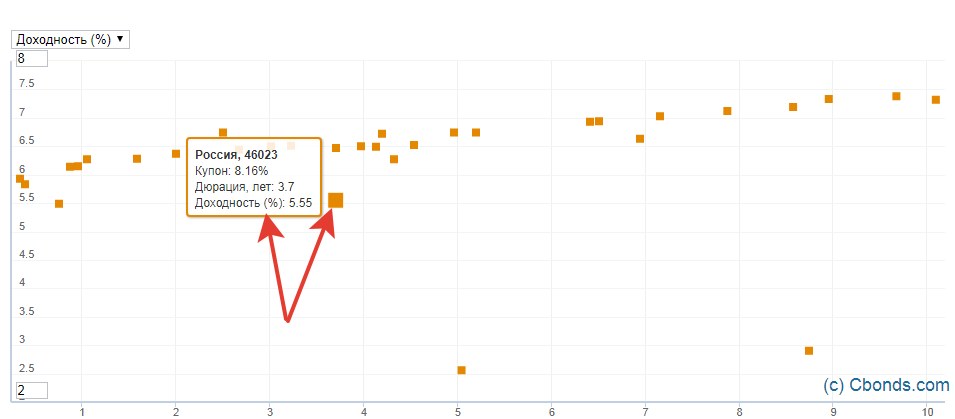
Если снова взять государственные облигации (ОФЗ) со сроком до погашения в пределах 10 лет, то можно легко провести визуальную оценку. При наведении на любую бумагу — выходит подсказка о названии и доходности облигации.

Помимо этого можно в самом торговом терминале (QUIK) самостоятельно построить кривую доходности.

Буквально в 3 шага:

1. В меню: «Создать окно» — «Все типы окон» или нажимаем F7
2. Выбираем в «Прочие» — «График доходности»
3. Отбираем нужные бумаги по которым нужно построить график (все или часть).

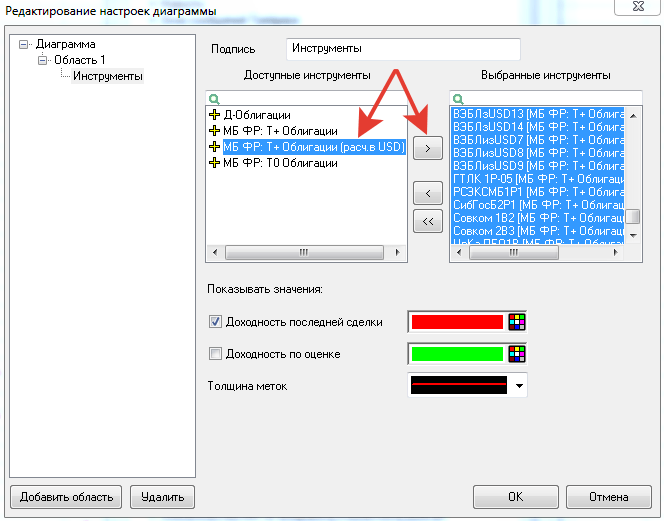
Возьмем для примера еврооблигации. Выбираем T+ Облигации (расч. в USD). И переносим в окно «Выбранные инструменты».

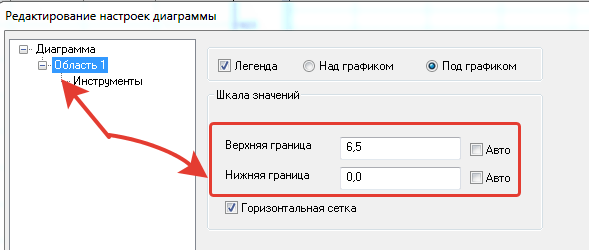
Для лучшего отображения ограничим доходность отображаемых бумаг до 6,5% годовых (чтобы исключить дефолтные облигации).

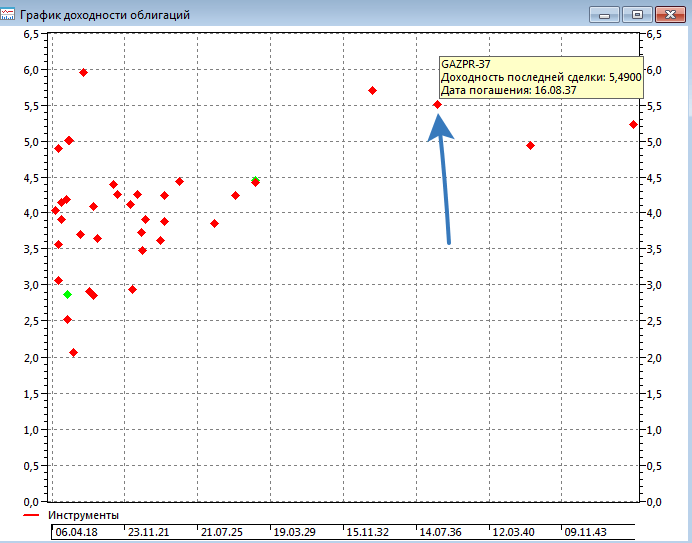
Выводим график доходности еврооблигаций.

Интересными выглядят евробонды Газпрома с погашением в 2037 году. При текущих рыночных ценах можно получать 5,5% годовых. Именно в долларах.

Что дает кривая доходности инвестору?

1. Быстрый анализ и поиск выгодных предложений. График доходности позволяет выявить недооцененные бумаги из общей массы торгуемых на рынке. Когда в списке доступных бумаг несколько десятков или даже сотен предложений очень трудно сравнивать их. Особенно учитывая, что все они имеют различные доходности и сроки погашения. Глядя на график доходности — инвестор видит всю картину целиком.
2. Наклон кривой подсказывает инвестору какие бумагу лучше брать в данный момент. В период повышения процентных ставок (нормальная кривая доходности) — лучше брать короткие бумаги. Так как «новые» поступающие на биржу бумаги будут иметь более высокую доходность. И «старые» облигации со временем будут терять в цене.
3. При тенденции к понижению процентных ставок (перевернутая кривая) — более выгодным будет вложиться в длинные бумаги, зафиксировав текущую доходность. Дополнительно, при снижении общего процента доходности на рынке, инвестор получит прибыль за счет роста рыночной цены его бумаг. В идеале, когда падение ставок прекратится — лучше продать все активы (намного выше номинала) не дожидаясь погашения. И купить коротких бумаг с текущей доходностью.

За обновлениями в этой и других статьях теперь можно следить на Telegram-канале: @vsedengy.

Источник

Методы построения кривой доходности

Понимание динамики временной кривой процентных ставок необходимо для финансовых институтов, специализирующихся на инструментах с фиксированным доходом. Например, если рассмотреть ипотечный рынок, то аналитическая система банков обычно требует знания изменений процентных ставок на ближайшие 360 месяцев. Формулы, известные для определения доходности к погашению, цен облигаций и срочных процентных ставок могут помочь аналитикам, при условии, что им известны ставки по бескупонным облигациям с аналогичными сроками погашениями. Многие рынки используют в качестве сравнительных показателей т.н. эталонные, государственные облигации (В России ГКО-ОФЗ).

Существуют два различных (с технической точки зрения) метода построения кривой доходности:

— Метод обратной связи (bootstrapping)

Перед любым методом необходимо определить задачи, стоящие перед использованием того или иного метода. Мы выделяем три задачи:

1) оценить временную структуру процентных ставок

2) объяснить выводы о виде кривой процентных ставок

3) проанализировать влияние процентных ставок на экономику

Метод «обратной связи»

Данный метод исходит из того, что нам известны процентные ставки по бескупонным облигациям с различным сроком погашения. Используя уравнение:

Где, — процентная ставка по бескупонным облигациям, — процентная ставка по купонным облигациям можно найти ставки по купонным облигациям. А если известны ставки по купонным облигациям, то необходимо решить обратную задачу, и такой метод называется методом обратной связи или (bootstrapping). Предположим, что проценты выплачиваются периодически. Величина равна ставкам по купонным облигация в первый период. Для того, чтобы найти , где n=2,3…, необходимо решить уравнение обратное (1) заново (выражаем из уравнения).

Необходимо еще раз подчеркнуть, что для решения уравнения обратного к (1) необходимо иметь значения ставок по бескупонным облигациям в правой части уравнения. Неизвестными являются ставки по бескупонным облигациям . Процесс поиска следующего значения бескупонной ставки можно легко систематизировать, достаточно иметь историю предыдущих значений и подсчитанные аннуитеты платежей. Достаточно добавлять новый член к уже имеющемуся значению этого параметра за предыдущий период. Как только будет построена кривая доходности бескупонных облигаций, то можно рассчитать кривую срочных процентных ставок для купонных и бескупонных облигаций. Необходимость в знании значений процентных ставок спот отпадает. (См. приложение)

Напомним общий алгоритм построения бескупонных кривых boot-strapping. Это итерационный процесс, который позволяет построить бескупонную кривую, используя в расчетах выпуски, начиная с самого короткого и заканчивая выпуском с максимальным сроком обращения.

1. Берется самый короткий выпуск. Оптимальным вариантом является облигация, по которой остался лишь один платеж, равный номиналу плюс последний купон. Для него рассчитывается доходность, которая и становится первой известной спот-ставкой.

Спот-ставки – наиболее используемые в моделях динамики процентных ставок вид ставок, представляющих собой доходность к погашению по бескупонной облигации с определенным сроком до погашения и рассчитываемая в конкретный момент времени. В более общем представлении спот-ставка – это процентная ставка, под которую в нулевой момент времени предоставляется некоторый заем на период времени, для которого и вычисляется ставка. Для более длинных выпусков (с числом невыплаченных купонов два и больше) необходимо оценить самую короткую спот-ставку посредством близких по кредитному качеству инструментов.

2. Далее расчеты происходят со следующей по сроку обращения (не по дюрации) облигацией. Первые платежи дисконтируются по уже известным спот-ставкам. Ставка для последней выплаты, включающей купон и номинал, подбирается так, чтобы сумма дисконтированных платежей была равна рыночной цене облигации с учетом накопленного купонного дохода.

Перебирая таким образом все обращающиеся выпуски облигаций, получаем бескупонную кривую.

Рисунок 1. Метод Bootstrapping. Поиск спот ставок.

Рисунок 2. Метод Bootstrapping. Временная структура процентых ставок

В качестве иллюстрации метода приведен пример расчета для облигаций с разными купонными выплатами ранжированные по возрастанию дюрации.

Метод интерполяции

Если одно из значений процентных ставок по купонным облигациям отсутствует, то использование метода обратной связи не позволит определить ни процентную ставку по бескупонной облигации, ни процентные ставки в следующие периоды. В таком случае используется другая техника-интерполяция. Интерполяция — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией кривой. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.[7]. Рассмотрим простейший вариант интерполяции- линейную интерполяцию. По двум известным значениям процентных ставок с разными сроками погашения – краткосрочная ставка, 3-х летняя, 6-ти летняя и т.д. рисуется прямая, соединяющая пару точек. Краткосрочная срочная процентная ставка зависит от первой производной функции кривой доходности бескупонных облигаций. Кусочно-линейная форма кривой доходности бескупонных облигаций означает, то функция краткосрочных срочных ставок имеет разрывы (не является непрерывной).

Рисунок 3 Кривые доходности на рынке спот и срочных рынках

Использование другого метода приближения функций-экстраполяции с помощью кубических сплайнов (spline extrapolation) обеспечивает непрерывность кривой доходности. Сплайн — кусочная функция, между каждой парой узлов которой имеет свой полином, и равенство производных в узлах. Это обеспечивает непрерывность второй производной на всем интервале интерполяции. Это также позволяет добиться большей гибкости и точности, большей чувствительности и возможность контроля гладкости. Данный метод заключается в разбиении всего интервала, охватывающего максимальный срок обращения государственных облигаций, на отдельные сегменты, каждый из которых содержит собственную аппроксимирующую процентную структуру функцию. Графически, эта функция будет иметь гладкий вид в отличие от кусочно-линейной.

Рисунок 4. Кривая процентных ставок, построенная методом интерполяции

После того, как определены методы соединения значений процентных ставок, возникает проблема в приближении к точным статистическим значением. Другими словами, если имеется точка, по которой нет данных, то выбранный метод должен предложить наиболее точный вариант оценки значения процентной ставки. Возникает двойственная проблема: гладкость против точности.

В данном разделе будут кратко перечислены основные методы. Для более подробного ознакомления указан список используемой литературы.

Способы приближения кривой доходности:

· Статические методы – приближение кривой доходности

o Параметрические методы (Нельсона-Зигеля, Свенсона)

o Непараметрические методы (Васичека-Фонга, синусоидально-экспоненциальные сплайны)

o 3-факторная модель Васичека с оценкой параметров фильтром Калмана.

o Общая афинная модель временной структуры.

o Подход, основанный на непосредственной эволюции цен.

Остановимся подробнее на методах, которые используется центральным банком для российского рынка долговых бумаг.

Метод Нельсона-Зигеля

В модели Нельсона-Сигеля мгновенная форвардная ставка равна:

где βi, τ- параметры, подлежащие определению. Соответствующая непрерывно

начисляемая процентная ставка имеет вид:

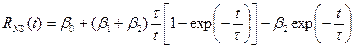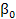
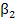
Где — параметр, отвечающий за вклад в модель влияние долгосрочной компоненты, — за краткосрочный компонент, — отвечает за среднесрочное влияние, τ – коэффициент затухания.

В модели Нельсона-Свенсона добавляются еще два параметра ,

Два дополнительных параметра отвечают за кривизну кривой и добавляет еще один «горб». Это позволяет добиться более точного приближения к данным.

Таблица 1. Применение методик в разных странах

Метод оценки:

параметрический Р

сплайны S

Центральный банк
Бельгия	P	Nelson-Siegel, Svensson
Великобритания	S	Waggoner
Германия	P	Svensson
Испания	P	Svensson
Италия	P	Nelson-Siegel
Канада	S	Merrill Lynch
Норвегия	P	Svensson
США	S	Fisher-Nychka-Zervos [8]
Финляндия	P	Nelson-Siegel
Франция	P	Nelson-Siegel, Svensson
Швейцария	P	Svensson
Швеция	S&P	Svensson
Япония	S	Fisher-Nychka-Zervos

Методика расчета кривой доходности на российском рынке предполагает модифицированную модель Нельсона- Свенсона с корректирующими добавками (для непрерывно начисляемой процентной ставки):

В рамках данной модели G—кривая однозначно определяется набором из 7 параметров: .

Вектор параметров G—кривой 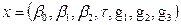пересчитывается после совершения каждой сделки с облигациями, для которой выполняются следующие условия:

— выпуск облигаций входит в базу расчета;

— до погашения выпуска облигаций остается не менее 30 календарных дней.

Методика пересчета параметров G-кривой[9]

Вектор параметров G—кривой пересчитывается после совершения каждой сделки с облигациями, для которой выполняются следующие условия:

— выпуск облигаций входит в базу расчета;

— до погашения выпуска облигаций остается не менее 30 календарных дней.

Пересчет параметров G—кривой осуществляется следующим образом. Пусть — значение вектора после обработки сделки с номером , — доходность сделки с номером . Тогда новый вектор параметров получается в результате следующих шагов:

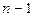
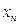
1) Для выпуска облигаций, с которым прошла сделка, по формуле для каждой даты выплат рассчитывается дисконтный коэффициент и определяется расчетная цена выпуска:

— количество предстоящих выплат по данному выпуску,

— соответствующие объемы выплат, выраженные в процентах от непогашенной части номинальной стоимости выпуска.

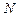
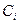
2) Определяется расчетная доходность к погашению по процедуре, установленной на рынке ГКО-ОФЗ, исходя из расчетной цены .

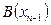
3) Численным методом рассчитывается вектор частных производных функции в точке .

4) По-компонентно рассчитывается новая оценка :

(4)

— номера компонентов,

, (5)

— среднеквадратическое отклонение погрешности оценки параметра ,

— дисперсия погрешности наблюдения, расчет которой приведен в разделе 7 настоящей Методики.

Функция обозначает знак (плюс или минус) выражения, находящегося в скобках. В случае значительного отличия от для предотвращения резкой, скачкообразной реакции кривой величина ограничивается способом, приведенным в разделе 6 настоящей Методики.

5) если , т.е. если параметр стал меньшим или равным 0,3 — расчеты, осуществленные в соответствии с пунктом 4) настоящего раздела, аннулируются; обнуляется и снова выполняется пункт 4) настоящего раздела. После этого параметру возвращается прежнее значение.

Из оценки при совершении следующей сделки получается оценка и так далее, т.е. алгоритм рекуррентный.

Кроме того, существуют также ограничения на величину спреда для каждого выпуска облигаций и нормированные границы по выпуску облигаций. Также учитывается «вес» сделки или объем сделки. Для сглаживания кривой применяют фильтр Калмана и многомерное экспоненциальное сглаживание.[10]

В настоящее время некоторые финансовые организации и коммерческие банки в России используют различных виды спредов доходности при оценке справедливой стоимости облигаций, а именно:[11]

— Номинальный спред (облигация\облигация)

— Z-спред (спред к кривой бескупонных доходностей, который учитывает форму кривой доходности)

— Относительный спред (облигации / доходность к погашению)

Теперь постараемся ответить на вопрос, почему же кривая доходности имеет такой вид. Для этого сравним два графика кривой доходности на две даты: докризисная и текущая.

Рисунок 5. КПД по ОФЗ на 18 декабря 2009 года

Рисунок 6. КПД по ОФЗ на 18 декабря 2008 года

Дата добавления: 2020-04-08 ; просмотров: 248 ; Мы поможем в написании вашей работы!

Источник