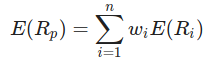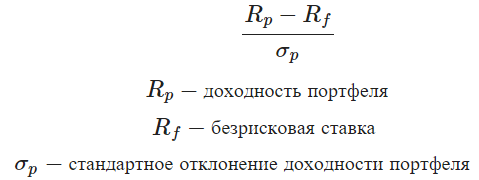Портфель максимальной доходности марковица

Оптимизации портфеля с помощью Python и PyPortfolioOpt

Портфельная теория Марковица(далее ПТМ) (Modern portfolio theory) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории.

Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.

Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.

Марковиц постоянно занимается усовершенствованием своей теории и в 1959 году выпускает первую посвящённую ей монографию «Выбор портфеля: эффективная диверсификация инвестиций».

В 1990 году, когда Марковицу вручают Нобелевскую премию, выходит книга «Средне-дисперсионный анализ при выборе портфеля и рынка капитала» ссылка.

Основа модели

1. Ожидаемая доходность портфеля(Portfolio Expected Return)

Ожидаемая доходность портфеля будет зависеть от ожидаемой доходности каждого из активов, входящих в него. Такой подход позволяет снизить риск за счет диверсификации и одновременно максимизировать доход инвестора, поскольку убытки по одним инвестициям будут компенсированы доходом по другим.

Ожидаемая доходность портфеля представляет собой суммарную ожидаемую доходность входящих в него ценных бумаг, взвешенную с учетом их доли в портфеле.

2. Дисперсия портфеля (Portfolio Variance)

Дисперсия портфеля — это процесс, который определяет степень риска или волатильности, связанной с инвестиционным портфелем. Основная формула для расчета этой дисперсии фокусируется на взаимосвязи между так называемой дисперсией доходности и ковариацией, связанной с каждой из ценных бумаг, найденных в портфеле, а также с процентом или частью портфеля, который представляет каждая ценная бумага.

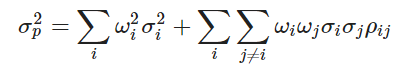
3. Коэффициент Шарпа (Sharpe Ratio)

Коэффициент Шарпа измеряет доходность инвестиций по отношению к безрисковой ставке (казначейской ставке) и степени риска. В целом, более высокое значение коэффициента Шарпа указывает на лучшие и более прибыльные инвестиции. Таким образом, если сравнивать два портфеля с одинаковыми рисками, то при прочих равных условиях было бы лучше инвестировать в портфель с более высоким коэффициентом Шарпа.

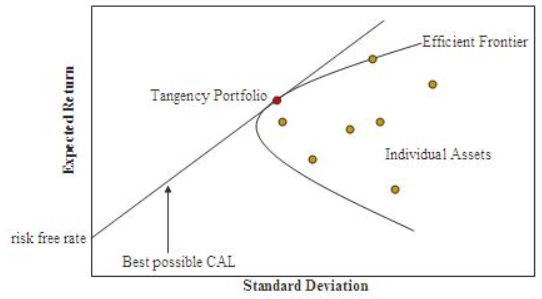
4. Эффективная граница (The Efficient Frontier)

Определение и рисунок из Википедии:

Граница эффективности (англ. Efficient frontier) в портфельной теории Марковица — инвестиционный портфель, оптимизированный в отношении риска и доходности. Формально границей эффективности является набор портфелей, удовлетворяющих такому условию, что не существует другого портфеля с более высокой ожидаемой доходностью, но с таким же стандартным отклонением доходности. Понятие границы эффективности было впервые сформулировано Гарри Марковицем в 1952 году в модели Марковица.

Портфель может быть охарактеризован как «эффективный», если он имеет максимально возможный ожидаемый уровень доходности для своего уровня риска (который представлен стандартным отклонением доходности портфеля). Так, на график соотношения риска и доходности может быть нанесена любая возможная комбинация рискованных активов, и совокупность всех таких возможных портфелей определяет регион в этом пространстве. При отсутствии в портфеле безрискового актива граница эффективности определяется верхней (восходящей) частью гиперболы, ограничивающей область допустимых решений для всех соотношений активов в портфеле.

В случае же, если в портфель может быть включён безрисковый актив, граница эффективности вырождается в отрезок прямой линии, исходящий от значения доходности безрискового актива на оси ординат (ожидаемая доходность портфеля) и проходящий по касательной к границе области допустимых решений. Все портфели на отрезке между собственно безрисковым активом и точкой касания состоят из комбинации безрискового актива и рисковых активов, в то время как все портфели на линии выше и справа от точки касания образуются короткой позицией в безрисковом активе и инвестированием в рисковые активы.

Оптимизация портфеля на Python

1. Импорт необходимых библиотек

2. Получение данных по акциям из интернета

Сначала установим опять пакет, который не входит в стандартный набор. Он позволяет получить данные по акциям с сайта yahoo.

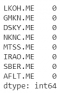
Тикеры, которые будут использоваться для анализа — одна из компаний входящих в лидеры в своем секторе.

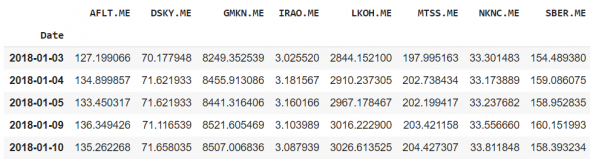
Дальше необходимо проверить есть ли среди полученных значений NaN. В случае их наличия они будут мешать дальнейшему исследованию. Для того, чтобы это решить, необходимо рассмотреть или иную акцию, или заменить их для примера средней ценой между днем до и после значения NaN.

3. Расчеты

Перейдем к расчетам по оптимизации портфеля и начнем с определения ожидаемой доходности и дисперсии портфеля. Далее сохраним значения весов портфеля с максимальным коэффициентом Шарпа и минимальной дисперсией.

OrderedDict([(‘AFLT.ME’, 0.0), (‘DSKY.ME’, 0.22606), (‘GMKN.ME’, 0.48796), (‘IRAO.ME’, 0.0), (‘LKOH.ME’, 0.0), (‘MTSS.ME’, 0.02953), (‘NKNC.ME’, 0.25645), (‘SBER.ME’, 0.0)])

Необходимо обратить внимание, что если изменить weight_bounds=(0,1) на weight_bounds=(-1,1), то в портфеле будут учитываться и короткие позиции по акциям.

Дальше посмотрим общие характеристики по портфелю.

Expected annual return: 37.1%
Annual volatility: 20.7%
Sharpe Ratio: 1.70
(0.37123023494063007, 0.20717177784552962, 1.695357536597058)

Теперь посмотрим портфель с минимальной волатильностью:

OrderedDict([(‘AFLT.ME’, 0.02876), (‘DSKY.ME’, 0.24503), (‘GMKN.ME’, 0.10403), (‘IRAO.ME’, 0.0938), (‘LKOH.ME’, 0.01168), (‘MTSS.ME’, 0.41967), (‘NKNC.ME’, 0.09704), (‘SBER.ME’, 0.0)])

Expected annual return: 24.0%Annual volatility: 16.9%Sharpe Ratio: -0.18(0.239915644698749, 0.16885732511472468, -0.17816434839774456)

4. Построение графика эффективных границ

Заключительным шагом является построение эффективной границы для визуального представления и расчет распределения активов.

Анализ произведем для суммы в 100 000 рублей.

Первым этапом посчитаем портфель с минимальной волатильностью:
<'AFLT.ME': 41, 'DSKY.ME': 181, 'IRAO.ME': 1765, 'LKOH.ME': 1, 'MTSS.ME': 127, 'NKNC.ME': 107>Осталось денежных средств после построения портфеля с минимальной волатильностью составляет 6152.03 рублей

Вторым шагом портфель с максимальным коэффициентом Шарпа:

<'DSKY.ME': 167, 'GMKN.ME': 2, 'MTSS.ME': 9, 'NKNC.ME': 283>Leftover Fund value in$ after building Max Sharpe ratio portfolio is $1319.05 Осталось денежных средств после построения портфеля с максимальным коэффициентом Шарпа 1319.05 рублей

В результате нам предлагается купить для оптимального портфеля 167 акций Детского мира, 2 акции Норильского никеля, 9 акций МТС и 283 акцию Нижнекамскнефтехим. В результате у нас еще останется 1319 рублей.

Еще раз напоминаю, что все вышеприведённое не является инвестиционной рекомендацией, а только поводом к размышлению.

Источник

Портфельная теория Марковица. Формирование инвестиционного портфеля в Excel

Приведем пример формирования инвестиционного портфеля по модели Г. Марковица с помощью программы Excel, разберем достоинства и недостатки данной модели в современной экономике и пути их решения.

Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.

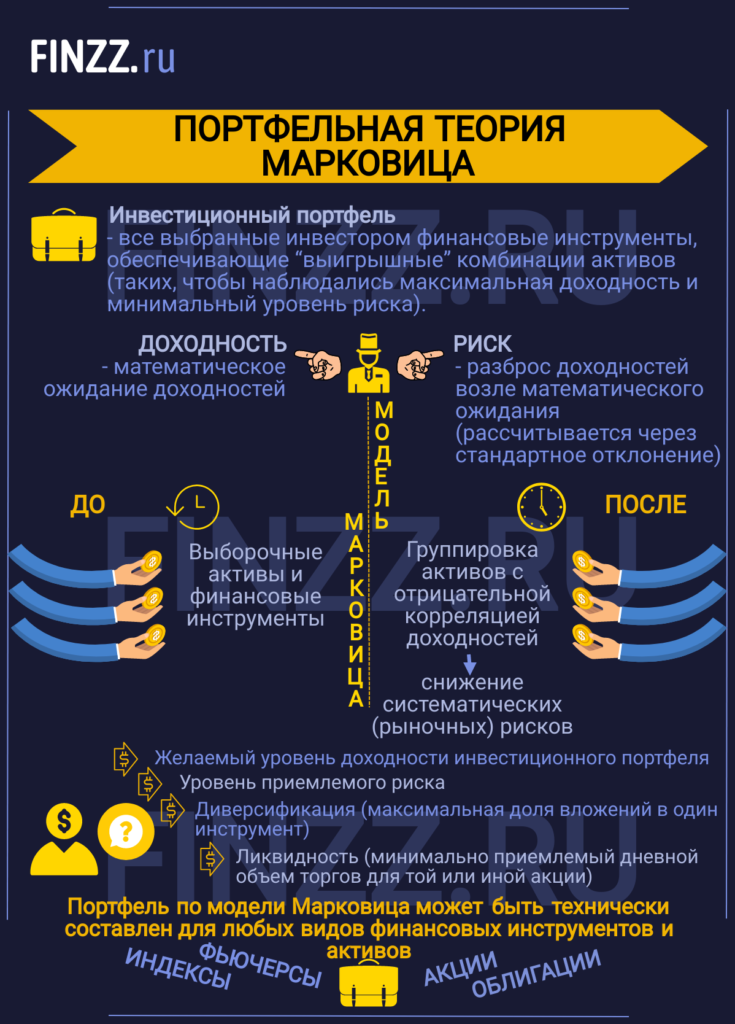
Инфографика: Портфельная теория Марковица (основная информация)

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Модель Марковица

Г. Марковиц в 1952 году впервые предложил математическую модель формирования инвестиционного портфеля. В основе его модели лежат два ключевых показателя любого финансового инструмента: доходность и риск, которые были количественно измерены. Доходность по модели представляет собой математическое ожидание доходностей, а риск определяется как разброс доходностей возле математического ожидания и рассчитывается через стандартное отклонение.

До модели Г. Марковица инвестирование происходило, как правило, в выборочные активы или финансовые инструменты, предложенная же им модель позволила снизить систематические (рыночные) риски за счет группировки активов с отрицательной корреляцией доходностей.

Следует заметить универсальность модели, так инвестиционный портфель может быть технически составлен для любых видов финансовых инструментов и активов: акций, облигаций, фьючерсов, индексов, недвижимости и т.д.

★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Цели формирования инвестиционного портфеля

Выделяют две инвестиционные стратегии при формировании портфеля:

► Максимизации доходности инвестиционного портфеля при ограниченном уровне риск.

► Минимизация риска инвестиционного портфеля при минимально допустимом уровне доходности.

Расчет доходности инвестиционного портфеля Марковица

Общая доходность портфеля будут представлять собой взвешенную сумму доходностей каждого отдельного финансового инструмента (актива):

где:

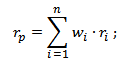
r_p – доходность инвестиционного портфеля;

w – доля i-го финансового инструмента в портфеле;

r_i – доходность i-го финансового инструмента.

Оценка риска инвестиционного портфеля Марковица

В модели Г. Марковица риск отдельно взятого финансового инструмента рассчитывается как стандартное отклонение доходностей. Для расчета общего риска портфеля необходимо отразить их совокупное изменение и взаимное влияние (через ковариацию), для этого воспользуемся следующей формулой:

где:

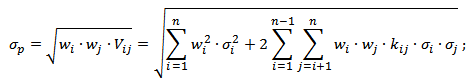
σp – риск инвестиционного портфеля;

σ_i – стандартное отклонение доходностей i-го финансового инструмента;

k_ij – коэффициент корреляции между I,j-м финансовым инструментом;

w_i – доля i-го финансового инструмента (акций) в портфеле;

V_ij – ковариация доходностей i-го и j-го финансового инструмента;

n – количество финансовых инструментов инвестиционного портфеля.

Эконометрический вид модели Марковица

Для того чтобы сформировать инвестиционный портфель необходимо решить оптимизационную задачу. Существует два вида задач: поиск долей акций в портфеле для достижения максимальной эффективности при заданном уровне риска (σ_p) и минимизация риска при заданном уровне доходности портфеля (r_p). Помимо этого на уравнения накладываются дополнительные очевидные ограничения: сумма долей активов должна быть равна 1 и сами доли активов должны быть положительными.

В таблице ниже показаны формулы и наложенные на них ограничения для поиска оптимальных долей финансовых инструментов (акций).

Портфель Марковица минимального риска	Портфель Марковица максимальной эффективности

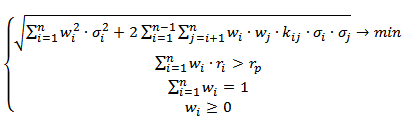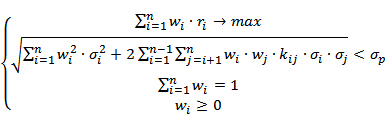★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Пример формирования инвестиционного портфеля Марковица в Excel

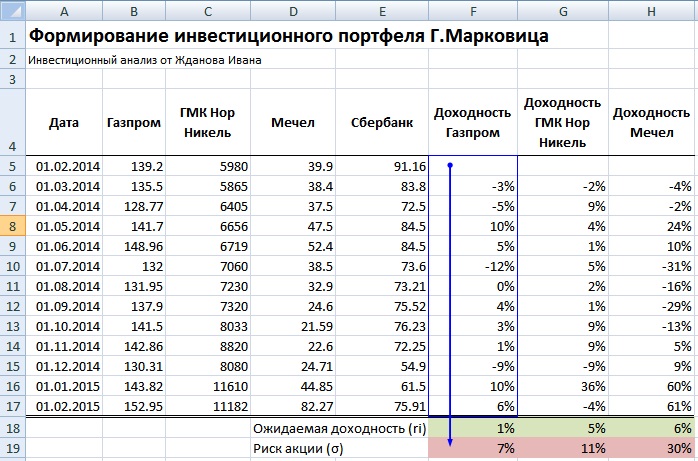
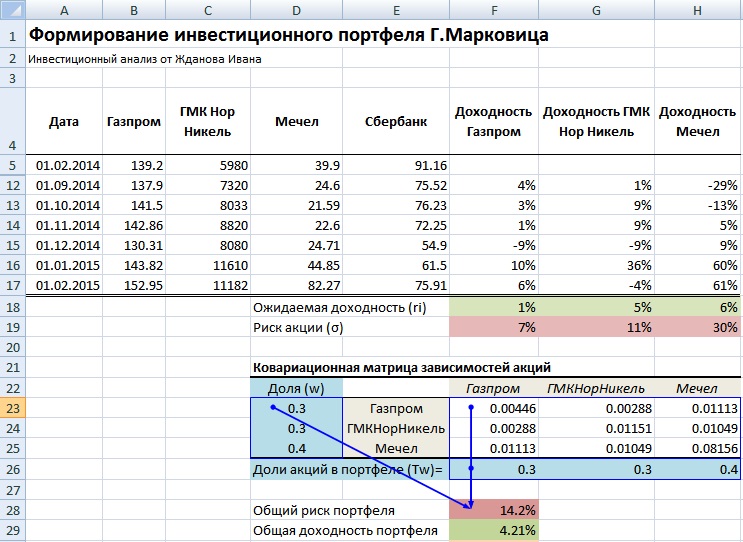
Рассмотрим наглядный пример формирования инвестиционного портфеля по модели Г. Марковица в программе Excel. Наш портфель будет состоять из четырех отечественных акций: ОАО «Газпром» (GAZP), ОАО «Норильский никель» (GMKN), ОАО «Мечел» (MTLR) и ОАО «Сбербанк» (SBER). Были взяты акции различных секторов: нефтегазового, промышленного и финансового, такой выбор увеличивает диверсификацию портфеля и снижает его рыночный риск.

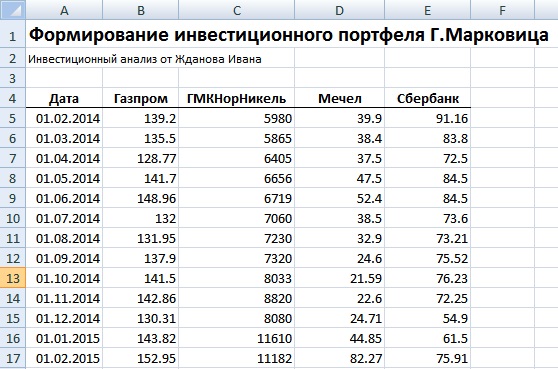
Рекомендуется брать период рассмотрения динамики изменения стоимости акций минимум один год. Это позволяет сделать более точный долгосрочный прогноз доходности и риска портфеля. На рисунке ниже показана ежемесячная стоимость акций за период с 01.02.2014 – 01.02.2015г.

Котировки акций Газпрома, ГМКНорНикеля, Мечела и Сбербанка

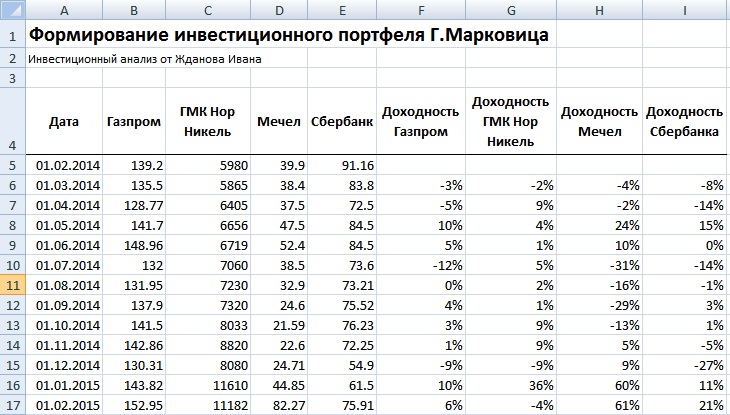
На следующем этапе формирования портфеля необходимо рассчитать ежемесячные доходности по каждой акции. Для этого воспользуемся формулой процентов в Excel:

Доходность Газпром =LN(B6/B5)

Доходность ГМКНорНикель =LN(C6/C5)

Доходность Мечел =LN(D6/D5)

Доходность Сбербанк =LN(E6/E5)

Расчет ежемесячных доходностей акций для модели Марковица в Excel

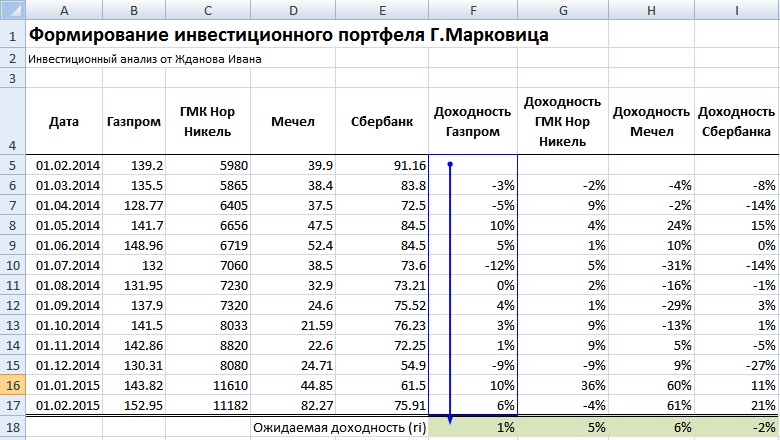
Далее определяем математическое ожидание доходностей по каждой акции, для этого найдем среднеарифметическое значение за весь период. Ожидаемая доходность по каждой акции будет следующая:

Ожидаемая доходность Газпром =СРЗНАЧ(F5:F17)

Ожидаемая доходность ГМКНорНикель =СРЗНАЧ(G5:G17)

Ожидаемая доходность Мечел =СРЗНАЧ(H5:H17)

Ожидаемая доходность Сбербанк =СРЗНАЧ(I5:I17)

Оценка ожидаемой доходности акций портфеля в Excel

Доходность акции ОАО «Сбербанк» имеет отрицательное ожидание доходности, поэтому ее следует исключить из портфеля. Оценка риска каждой акции – это ее изменчивость (волатильность) по отношению к математическому ожиданию доходностей.

Формула расчета риска акций следующая:

Риск Газпром =СТАНДОТКЛОН(F5:F17)

Риск ГМКНорНикель =СТАНДОТКЛОН(G5:G17)

Риск Мечел =СТАНДОТКЛОН(H5:H17)

Оценка риска по акции инвестиционного портфеля в Excel

Мы получили первоначальные необходимые данные для оценки долей данных акций в инвестиционном портфеле. Для оценки уровня риска всего инвестиционного портфеля воспользуемся надстройкой в Excel. Для этого зайдем в Главном меню → «Данные» → «Анализ данных» → «Ковариация».

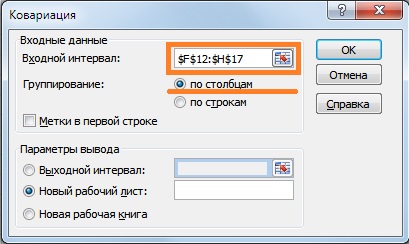
Далее в появившемся окне необходимо найти ковариации между доходностями акций. Указываем входной интервал – ежемесячных доходностей акций, а в опции «Группирование» выбираем функцию «по столбцам».

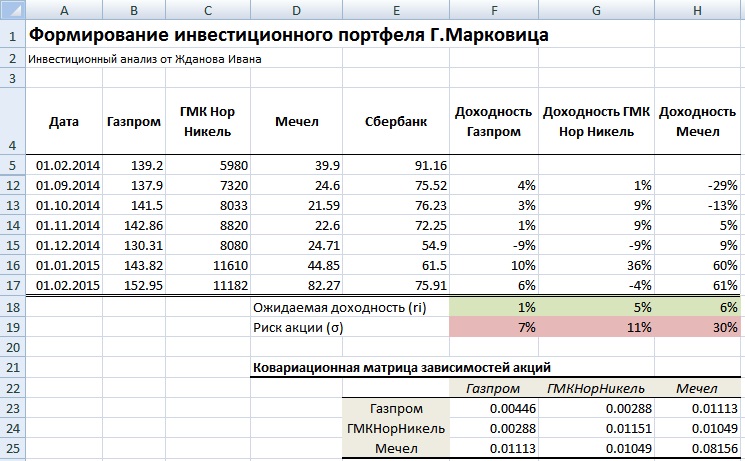
Результатом будет таблица ковариаций доходностей акций между собой. Расположим ее ниже под таблицей. Можно заметить, что диагональные значения представляют собой дисперсию доходностей акций.

Пример расчета ковариационной матрицы для инвестиционного портфеля Марковица в Excel.

Для расчета общего риска портфеля воспользуемся формулой рассмотренной выше и для этого нам необходимо перемножить доли весов акций между собой и значения ковариаций этих акций. Для того чтобы понять принцип расчета, установим доли акций 0.3, 0.3 и 0.4 и рассчитаем общий риск портфеля. Доходность портфеля рассчитывается как средневзвешенная сумма доходностей отдельных акций. Так как мы будем перемножать матрицы необходимо транспонировать столбец с долям (wT). Формула расчета риска инвестиционного портфеля будет иметь следующий вид:

Общий риск инвестиционного портфеля =КОРЕНЬ(МУМНОЖ(МУМНОЖ(F26:H26;F23:H25);D23:D25))

Общая доходность инвестиционного портфеля =F18*F26+G18*G26+H18*H26

Формирование инвестиционного портфеля минимального риска

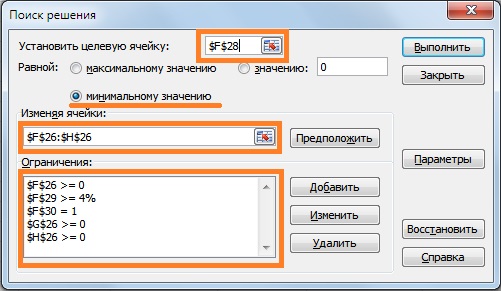
Для данной задачи необходимо определить минимальный уровень допустимой доходности портфеля (r_p). Возьмем r_p ≥ 4%. При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню Excel → «Данные» → «Поиск решений», а также введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.

В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля), ввести, какие параметры необходимо изменять (доли акций) и текущие ограничения. Целевая ячейка – это ячейка с формулой общего риска инвестиционного портфеля. Программа будет изменять значения долей акций при выставленных ограничениях. Формула ограничения размера доли в портфеле будет иметь следующий вид:

Ограничение на сумму долей акций (F30) =СУММ(F26:H26)

Расчет долей акций в инвестиционном портфеле в Excel

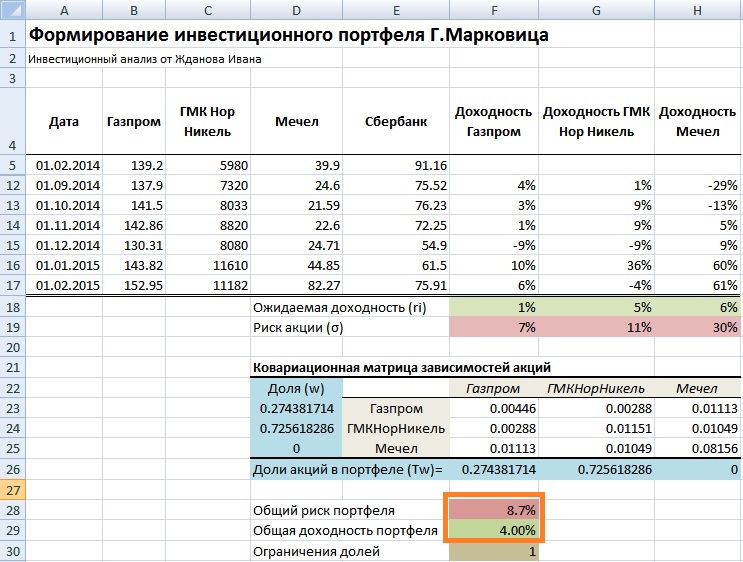
В результате мы получаем следующий расчет общего риска и доходности портфеля. Общий риск портфеля составил 8,7%, тогда как общая доходность 4%. Доли акций Газпрома получились равными 27%, доли ГМКНорНикель 73% и Мечела 0%. При заданных условиях эффективнее будет формирование портфеля из двух акций ОАО «Газпром» и ОАО «ГМКНорНикель».

Формирование инвестиционного портфеля Марковица в Excel. Пример расчета для минимального риска

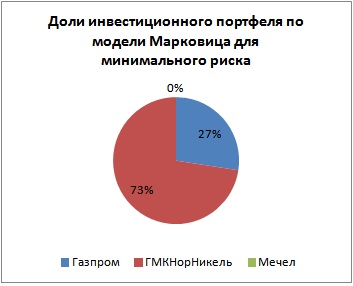
Визуально доли портфеля будут соотноситься следующим образом.

Формирование эффективного инвестиционного портфеля

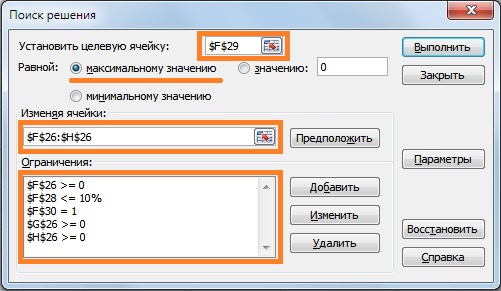
Вторая задача, которая решается на основе модели Г. Марковица – посторонние портфеля с максимальным уровнем доходности и ограниченным уровнем риска. Разберем на примере данную задачу. Установим максимально допустимый уровень риска портфеля σ_p≤10%. С помощью надстройки «Поиск решений» определим доли акций в данной интерпретации задачи. Целевая ячейка будет ячейка с формулой доходности портфеля, ее следует максимизировать, изменяя значения долей акций при ограничениях по риску. На рисунке ниже показаны основные параметры для формирования портфеля с максимальной доходностью.

Оптимизация инвестиционного портфеля для максимизации доходности

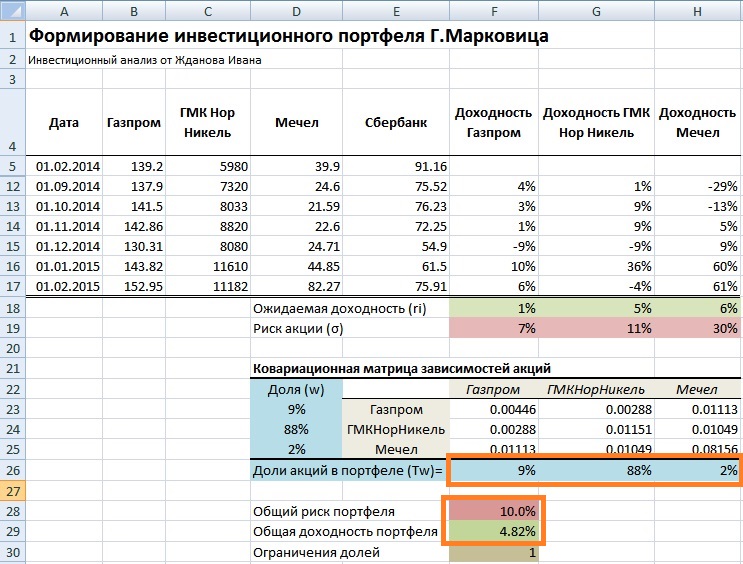
В результате мы получили доли акций в инвестиционном портфеле: 9% акций ОАО «Газпром», 88% акций ОАО «ГМКНорНикель» и 2% акций ОАО «Мечел». Общий риск портфеля не превысил 10%, а доходность составила 4,82%.

Формирование инвестиционного портфеля Марковица в Excel. Пример оценки для максимизации доходности акций

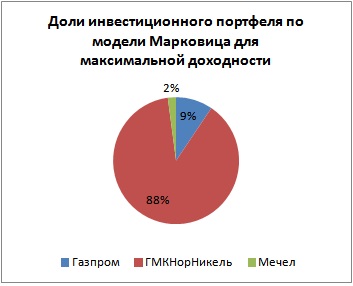
Визуально доли инвестиционного портфеля будут соотноситься следующим образом.

Достоинства и недостатки модели Г. Марковица

Рассмотрим ряд недостатков присущих модели Г. Марковица.

• Данная модель была разработана для эффективных рынков капитала, на которых наблюдается постоянный рост стоимости активов и отсутствуют резкие колебания курсов, что было в большей степени характерно для экономики развитых стран 50-80-х годов. Корреляция между акциями не постоянна и меняется со временем, в итоге в будущем это не уменьшает систематический риск инвестиционного портфеля.
• Будущая доходность финансовых инструментов (акций) определяется как среднеарифметическое. Данный прогноз основывается только на историческом значении доходностей акции и не включает влияние макроэкономических (уровень ВВП, инфляции, безработицы, отраслевые индексы цен на сырье и материалы и т.д.) и микроэкономических факторов (ликвидность, рентабельность, финансовая устойчивость, деловая активность компании).
• Риск финансового инструмента оценивается с помощью меры изменчивости доходности относительно среднеарифметического, но изменение доходности выше не является риском, а представляет собой сверхдоходность акции.

Многие из данных недостатков модели были решены последователями: прогнозирование доходности с помощью многофакторных моделей (Ю. Фама, К. Френч, Росс и др.), нейронных сетей; оценка риска на основе моделей ARCH, GARCH и т.д. Следует отметить одно из главных достоинств модели Г. Марковица: систематизация подхода к формированию инвестиционного портфеля и управление его доходностью и риском.

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Резюме

В данной статье мы рассмотрели, как с помощью Excel можно сформировать инвестиционный портфель по модели Г. Марковица и решить две классические задачи: максимизация доходности портфеля при минимальном риске и минимизация риска при заданной доходности. Портфель Марковица позволяет снизить систематические риски за счет комбинации различных активов. Несмотря на сложности использования данной модели в современной экономике данная модель применима для таких низковолатильных активов как недвижимость, облигации товарные фьючерсы и т.д. В настоящее время сократился срок пересмотра активов в портфеле, так если раньше он мог составлять год, то сейчас это 2-6 месяцев. С вами был Иван Жданов, спасибо за внимание.

Автор: к.э.н. Жданов Иван Юрьевич

Источник