Поиск оптимального решения доходности

«Поиск решения» составит оптимальную депозитную программу

Цели: подобрать вариант размещения временно свободных денежных средств на банковских депозитах, обеспечивающий компании максимальный доход.

Как действовать: задать условия и ограничения на размещение депозитов в виде формул в Excel и воспользоваться надстройкой «Поиск решения».

Зачастую на расчетных счетах компаний, особенно тех, чей бизнес подвержен влиянию сезонных факторов, аккумулируются временно свободные денежные средства. Разумеется, не перевести такие излишки денег, например, на депозит — просто расточительство. Возможно, банковские депозиты не лучший инструмент для инвестирования, и все же они позволят получить некоторый дополнительный доход на вложенные деньги, хотя бы компенсировать инфляционные потери.

Вопрос в том, как правильно распределить средства между банками, как подобрать срок, на который они будут отвлечены из оборота, определиться с суммой и банком. Выстроить оптимальную с точки зрения дополнительных доходов депозитную программу поможет Excel, а точнее один из его встроенных инструментов под названием «Поиск решения».

Сформулировать ограничения

Суть работы инструмента «Поиск решения» сводится к тому, что программа перебирает все возможные варианты решений с учетом заданных ограничений и выбирает из них наилучшее. Инструмент полностью оправдывает свое название. Сразу оговоримся, что «Поиск решения» можно использовать в отношении практически не ограниченного спектра оптимизационных задач — главное, правильно задать условия. В нашем случае речь идет о подборе оптимальной структуры размещения свободных денежных средств на депозитах в нескольких банках с разными ставками доходности.

Для начала разберемся с тем, что подразумевается под оптимальной структурой размещения. В чем цель оптимизации? Иначе говоря, по каким критериям Excel будет проводить сравнение и выбор? Чаще всего таким показателем служит ожидаемый доход. То есть смысл оптимизационной задачи сводится к поиску такого решения, которое обеспечит компании максимальный доход по депозитам.

Теперь нужно задать ограничения. Вся информация заносится в одну или несколько таблиц, например, таких, как показано на рисунке 1 на стр. 75 (для простоты восприятия ячейки, в которые вносятся ограничения, выделены голубым фоном). Итак, какие условия можно и нужно задать программе.

Во-первых, это имеющиеся на счетах в разных банках суммы временно свободных средств и время, в течение которого эти деньги не потребуются компании. На рисунке 1 это диапазоны ячеек H12:K12 и H11:K11 соответственно. Во-вторых, нужно указать ставки по депозитам, которые предлагают банки-партнеры для разных сроков размещения денег (в процентах годовых — диапазон ячеек D17:G25). Наконец, в-третьих, предстоит ввести сведения об объемах неиспользованных лимитов по каждому из банков (диапазон ячеек С17:С25). Другими словами, ограничения на размер депозита, определяемые в зависимости от надежности конкретной кредитной организации (на усмотрение менеджмента компании). Согласитесь, было бы неоправданно рискованно все деньги положить в один банк, особенно если речь идет о действительно больших суммах средств.

Подобрать лучшее решение

Итак, после того как определена цель оптимизации и основные ограничения, остается сделать совсем немного, прежде чем запускать процедуру «Поиск решения». Нужно на том же листе Excel создать табличные блоки для вывода промежуточных и итоговых расчетных данных. В примере на рисунке 1 это разделы «Суммы к размещению на депозитах по срокам в днях, руб.», «Итого размещено, руб.», «Доход от средств, размещенных на депозитах, по срокам в днях, руб.» и «Доходность от размещения на депозитах, итого».

Рисунок 1. Модель для построения оптимальной программы размещения депозитов компании

В блоке «Суммы к размещению на депозитах по срокам в днях, руб.» (диапазон ячеек H17:K25) будут отражены результаты — та самая оптимальная структура депозита (или депозитная программа). Excel заполнит эту часть таблицы сам.

Разделы «Итого размещено, руб.» (диапазон ячеек С17:С25) и «Доход от средств, размещенных на депозитах, по срокам в днях, руб.» (диапазон ячеек M17:P25) предназначены для вывода промежуточных расчетов. Здесь формулы придется вводить вручную. Сложного в них ничего нет. В первом разделе по каждому банку суммируются депозиты, во втором — вычисляется доход от размещенного вклада с учетом срока, суммы первоначального взноса и срока.

Целевой показатель «Доходность от размещения на депозитах, итого, руб.», который предстоит максимизировать, также расчетный. Это не что иное, как сумма доходов от всех вкладов (в примере использована следующая формула: «=СУММ(М17:Р25)»).

Рисунок 2. Условия и ограничения для поиска решений

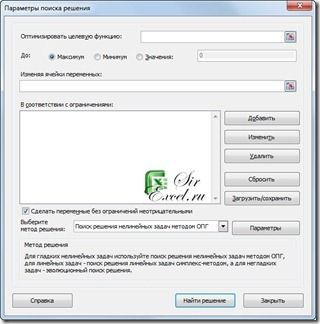
Теперь все готово. Запускаем процедуру «Поиск решения». Для этого нужно кликнуть по одноименной кнопке на вкладке панели инструментов «Данные» 1 . В появившемся диалоговом окне (см. рис. 2) указываем:

• целевую ячейку — критерий оптимизации. В нашем случае С30 — «Доходность от размещения на депозитах, итого, руб.»;
• направление оптимизации — минимальное, максимальное или определенное значение целевой ячейки. Разумеется, нас интересует максимальный доход от вкладов;
• диапазон, в котором будут отражаться результаты решения — суммы вкладов в различных банках (H17:K25).

И в этом же диалоговом окне задаем ограничения для возможных решений:

• все свободные денежные средства должны быть размещены на депозитах без остатка (Н27:К27 = Н12:К12);
• сумма вкладов в одном банке не может быть выше лимита, установленного для этой же кредитной организации (L17:L25

1 В Excel настройка «Поиск решения» по умолчанию не активна. Если в панели инструментов, на вкладке «Данные», нужная кнопка отсутствует, ее потребуется активизировать. Открыть меню с помощью кнопки «Office», выбрать в нем «Параметры Excel», в левой части появившегося диалогового окна кликнуть по пункту «Надстройки», затем Управление-Параметры Excel-Перейти-Поиск решения.

Источник

Поиск оптимального решения доходности

4 Поиск оптимального портфеля.

Согласно Марковицу, любой инвестор должен основывать свой выбор исключительно на ожидаемой доходности и стандартном отклонении при выборе портфеля. Таким образом, осуществив оценку различных комбинаций портфелей, он должен выбрать «лучший», исходя из соотношения ожидаемой доходности и стандартного отклонения этих портфелей. При этом соотношение доходность-риск портфеля остается обычным: чем выше доходность, тем выше риск.
Также, прежде чем приступить к формированию портфеля, необходимо дать определение термину «эффективный портфель». Эффективный портфель — это портфель, который обеспечивает: максимальную ожидаемую доходность для некоторого уровня риска, или минимальный уровень риска для некоторой ожидаемой доходности.
В дальнейшем будем находить эффективные портфели в среде Excel в соответствии со вторым принципом — с минимальным уровнем риска для любой ожидаемой доходности. Для нахождения оптимального портфеля необходимо определить допустимое множество соотношений «риск-доход» для инвестора, которое достигается путем построения минимально-дисперсионной границы портфелей, т.е. границы, на которой лежат портфели с минимальным риском при заданной доходности.

Рисунок 2.20 – Минимально – дисперсионная граница
На рисунке выше жирной линией отображена «эффективная граница», а большими точками отмечены возможные комбинации портфелей.
Эффективная граница — это граница, которая определяет эффективное множество портфелей. Портфели, лежащие слева от эффективной границы применить нельзя, т.к. они не принадлежат допустимому множеству. Портфели, находящиеся справа (внутренние портфели) и ниже эффективной границы являются неэффективными, т.к. существуют портфели, которые при данном уровне риска обеспечивают более высокую доходность, либо более низкий риск для данного уровня доходности.
Для построения минимально-дисперсионной границы и определения «эффективной границы» нам будут необходимы значения ожидаемых доходностей, рисков (стандартных отклонений) и ковариации активов. Имея эти данные можно приступить к нахождению «эффективных портфелей».
Начнем с расчета ожидаемой доходности портфеля по формуле:

(2.8)

где Хi – доля i-ой бумаги в портфеле;
E(ri) – ожидаемая доходность i-ой бумаги.
А затем определим дисперсию портфеля, в формуле которой используется двойное суммирование:

(2.9)

где — дисперсия портфеля;
— доли i-ой и j-ой бумаги в портфеле;
— ковариация доходностей бумаг i и j.
И как следствие найдем стандартное отклонение портфеля, которое является квадратным корнем из дисперсии по формуле (2.5)
Для наглядности приведем пример построения эффективной границы при помощи Microsoft Excel, а точнее при помощи встроенного в него компонента Поиск решения.
Зададим долю каждого актива в нашем первоначальном портфеле пропорционально их количеству. Следовательно, доля каждого актива в портфеле составит 1/3, т.е. 33%. Общая доля должна равняться 1, как для портфелей, в которых разрешены «короткие» позиции, так и для тех, в которых запреще-ны. Сам Марковиц запрещает открывать «короткие» позиции по активам, входящим в портфель, однако современная портфельная это разрешает. Если «короткие» позиции разрешены, то доля по активу будет отображена как -0.33 и средства, вырученные от его продажи, должны быть вложены в другой актив, таким образом, доля активов в портфеле в любом случае будет равняться 1.
Рассчитаем ожидаемую доходность, дисперсию и стандартное отклонение средневзвешенного портфеля:

Рисунок 2.21 – Вид с формулами
Как видно из таблицы, для определения дисперсии портфеля нужно просто просуммировать данные в ячейках B19-D19, а квадратный корень из значения ячейки C21 даст нам стандартное отклонение портфеля в ячейке C22. Произведение долей бумаг на их ожидаемую доходность даст нам ожидаемую доходность нашего портфеля, которая отражена в ячейке C23. Окончательный результат средневзвешенного портфеля представлен ниже.

Рисунок 2.22 – Вид со значениями
Средняя (ожидаемая) месячная доходность средневзвешенного портфеля 0,28% при риске 6,94%. Теперь можно применить тот самый второй принцип, о котором было написано выше, т.е. обеспечить минимальный риск при заданном уровне доходности. Для этого воспользуемся функцией «Поиск Решений» из меню «Сервис». Если нет, значит надо открыть «Сервис» выбрать «Надстройки» и установить «Поиск решений».
Запускаем «Поиск решений», в пункте «Установить указанную ячейку» указываем ячейку С22, которую будем минимизировать за счет изменения долей бумаг в портфеле, т.е. варьированием значений в ячейках A16-A18. Далее надо добавить два условия, а именно:
1) сумма долей должна равняться 1, т.е. ячейка A19 = 1,
2) задать доходность, которая нас интересует, к примеру, доходность 0.28% (ячейка С23), которая получилась при расчете средневзвешенного портфеля.
Так как мы запрещаем наличие «коротких» позиций по бумагам в меню «Параметры» надо установить галочку «Неотрицательные значения». Вот так должно выглядеть:

Рисунок 2.23 – Поиск решения

Рисунок 2.24 – Параметры поиска решений
В результате мы получаем:

Рисунок 2.25 – Результат при «Поиске решений»
Итак, задав «Поиск решений» найти минимальное стандартное отклонение при заданной ожидаемой доходности в 0,33% мы получили оптимальный портфель, состоящий на 83% из РАО ЕЭС, на 17% из Лукойла и на 0% из Ростелекома. Несмотря на то, что уровень доходности тот же, что и при средневзвешенном портфеле, риск снизился.

Источник

Поиск решения в excel – получение максимальной прибыли

Для начала скажу, что я зарабатываю через вот этого брокера , проверен он временем! А вот хороший пример заработка , человек зарабатывает через интернет МНОГО МНОГО МНОГО и показывает все на примерах, переходи и читай! Добавь страницу в закладки. А теперь читаете информацию ниже и пишите свой отзыв

Видео: Поиск решения. Задача о выборе инвестиций

Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.

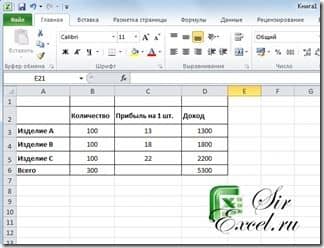
Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.

При решении данной задачи должны быть учтены следующие ограничения:

• общий объем производства – всего 300 изделий;
• должно быть произведено не менее 50 изделий А;
• должно быть произведено не менее 40 изделий В;
• должно быть произведено не более 40 изделий С.

1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.
2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)

и в окне “Поиск решений” ввести данные:

Видео: Урок 1.Поиск решения, оптимизация, оптимальный план производства

• в поле «Установить целевую ячейку» указать адрес D6;
• установить флажок «Равной максимальному значению»;
• в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
• в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300- B3>=50- B4>=40- B5 (Пока оценок нет)

Источник