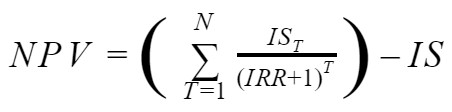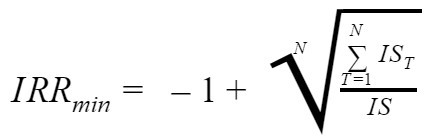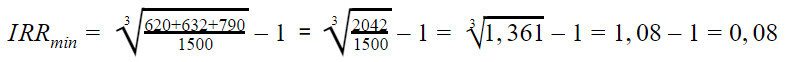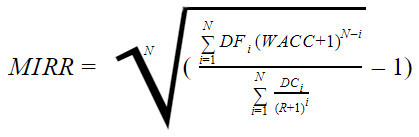Под нормой рентабельности инвестиций понимают значения коэффициента дисконтирования при котором

Внутренняя доходность (норма рентабельности)(Internal Rate of Return, IRR)

Под внутренней доходностью (нормой рентабельности инвестиции) (IRR) понимают значение коэффициента дисконтирования, при котором NPV проекта равен нулю:

IRR = r, при котором NPV = f(r) = 0.

Смысл расчета этого коэффициента при анализе эффективности планируемых инвестиций заключается в следующем:IRRпоказывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение IRRпоказывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любое предприятие финансирует свою деятельность, в том числе и инвестиционную, из различных источников. В качестве платы за пользование авансированными в деятельность предприятия финансовыми ресурсами оно уплачивает проценты, дивиденды, вознаграждения и т.п., т.е. несет некоторые обоснованные расходы па поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих расходов, можно назвать «ценой» авансированного капитала (CC). Этот показатель отражает сложившийся на предприятии минимум возврата на вложенный в его деятельность капитал, его рентабельность и рассчитывается по формуле средней арифметической взвешенной.

Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя CC (или цены источника средств для данного проекта, если он имеет целевой источник). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.

По сути IRR характеризует ожидаемую доходность проекта. Если IRR превышает цену капитала, используемого для финансирования проекта, это означает, что после расчетов за пользование капиталом появится излишек, который достается акционерам фирмы. Следовательно, принятие проекта, в котором IRR больше цены капитала, повышает благосостояние акционеров. С другой стороны, если IRR меньше цены капитала, и тогда реализация проекта будет убыточной для акционеров. Этим и объясняется полезность применения критерия IRR для оценки инвестиционных проектов.

Если: IRR > CC. то проект следует принять;

(4.11)

где: CFj — входной денежный поток в j-ый период,

CF0 — настоящее значение инвестиции.

Решая уравнение, находим IRR. Решение может быть только приближенным.

Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтирования r1 0 (f(r1) 0).

Точность вычислений обратно пропорциональна длине интервала (r1,r2), а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала минимальна (равна 1%), т.е. r1 и r2 — ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции с «+» на «-«):

r1 — значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. f(r1)=minr0>;

r2 — значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV, т.е. f(r2)=maxr

Источник

Внутренняя норма рентабельности инвестиций

Лipv = ? ciFt /(1 + г)’ — ? COF, /(1 + г)( = О,

IRR = г, при котором NPV^Ar) = 0.

Таким образом, IRR находится из уравнения

где CFj — входной денежный поток в j-й период,

INV — сумма инвестиции.

Смысл расчета этого коэффициента при анализе эффективности планируемых инвестиций заключается в следующем: IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом.

При NPV- 0 современная стоимость проекта (PV) равна по абсолютной величине первоначальным инвестициям /0, следовательно, они окупаются. В общем случае чем выше значение IRR, тем больше эффективность инвестиций. Значение IRR сравнивают с заданной нормой дисконта г. При этом если IRR > t\ то проект обеспечивает положительную NPV и доходность, равную IRR — г. Если IRR И/ЛСС, проект следует принять;

где г — некоторая базовая ставка процента.

Этот критерий также ориентирован в первую очередь на учет возможностей альтернативного вложения финансовых средств, поскольку он показывает не абсолютную эффективность проекта как таковую (для этого было бы достаточно неотрицательной ставки IRR), а относительную — по сравнению с операциями на финансовом рынке.

Показатель IRR может применяться также и для сравнения эффективности различных инвестиционных проектов между собой. Однако здесь простого сопоставления значений внутренней нормы рентабельности сравниваемых проектов может оказаться недостаточно. В частности результаты, полученные при сравнении эффективности инвестиционных проектов при помощи NPV- и IRR- методов, могу г привести к принципиальным различиям. Это обусловлено следующими обстоятельствами: для достижения абсолютной сопоставимости проектов необходимо применение так называемых дополнительных инвестиций, позволяющих устранить различия в объеме инвестированного капитала и сроках реализации проектов.

На практике сравнительный анализ инвестиционных проектов в большинстве случаев проводится простым сопоставлением значений внутренних норм рентабельности. Несмотря на определенную теоретическую некорректность, такой подход позволяет устранить влияние субъективного выбора базовой ставки процента на результаты анализа. Действительно, основная цель использования инструменгария дополнительных инвестиций заключается в попытке согласовать результаты сравнительного анализа при помощи NPV- и /AA-методов, точнее, привязать второе к первому, поскольку при таком подходе приоритет имеет чистый приведенный доход проекта. Кроме того, применение инструмента дополнительных инвестиций корректно только в случае срав-нительного анализа альтернативных, или взаимоисключающих, проектов, чю еще более сужает область его применения и делает совершенно непригодным для анализа инвестиционной программы.

В целом по сравнению с Л^РК-методом использование показателя внутренней нормы рентабе:1ьности связано с большими ограничениями: во-первых, для IRR-метода действительны все ограничения NPV- метода, т.е. необходимость изолированного рассмотрения инвестиционного проекта, необходимость прогнозирования денежных потоков на весь период реализации проекта и т.д.; во-вторых, сфера применения IRR-метода ограничена только областью чистых инвестиций.

Сравнение и /ЯД-мегодов. К сожалению МРУ- и /ЯЛ-методы могут конфликтовать друг с дротом. Рассмотрим это на конкретном примере.

Пример 5. Оценим сравнительную эффективность двух проектов с одинаковыми исходными инвестициями, но с различными входными денежными потоками. Исходные данные для расчета эффективности помещены в табл.

Таблица 8.3. Денежные потоки альтернативных проектов Год 0-й 1-й 2-й 3-й /«-й Проект А -1000 500 400 300 І 00 Проект В -1000 100 300 400 600

Для дальнейшего анализа используем так называемый ЛТ^-профиль — зависимость показателя МРУ от стоимости капитала проекта.

Рис. 8.4. yVPF-профили альтернативных проектов

Рассчитаем ИРУ для различных значений стоимости капитала (табл. 8.4).

Таблица 8.4. Показатели Л’? К для альтернативных проектов Год 0-й 5-й 10-й 15-й Проект А 300 180,42 78,82 8,33 Проект В 400 206,50 49,18 80,14

Графики ЛТ^-профилей для проектов представлены на рис. 8.4. Решив уравнения, определяющие внутреннюю норму доходности, получим: для проекта А IRR- 14,5%; для проекта В IRR= 11,8%.

Таким образом, по критерию внутренней нормы доходности предпочтение следует отдать проекту А, как имеющему большее значение IRR. В то же время NPV-метод дает вывод в пользу проекта В.

Проанализировав соотношение УУРК-профилей, которые имеют пересечение в точке j*, соответствующей в данном случае значению 7,2%, приходим к следующему выводу:

если г > г* оба метода лают одинаковый результат;

Источник

Метод внутренней ставки дохода. Под нормой рентабельности инвестиции (irr) понимают значение коэффициента дисконтирования, при котором npv проекта равен нулю:

IRR = r, при котором NPV = f(r) = 0.

Смысл расчета этого коэффициента при анализе эффективности планируемых инвестиций заключается в следующем: IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любое предприятие финансирует свою деятельность, в том числе и инвестиционную, из различных источников. В качестве платы за пользование авансированными в деятельность предприятия финансовыми ресурсами оно уплачивает проценты, дивиденды, вознаграждения и т.п., т.е. несет некоторые обоснованные расходы на поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих расходов, можно назвать «ценой» авансированного капитала (CC). Этот показатель отражает сложившийся на предприятии минимум возврата на вложенный в его деятельность капитал, его рентабельность и рассчитывается по формуле средней арифметической взвешенной.

Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя CC (или цены источника средств для данного проекта, если он имеет целевой источник). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.

Если: IRR > CC. то проект следует принять;

Точность вычислений обратно пропорциональна длине интервала (r1,r2), а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала минимальна (равна 1%), т.е. r1 и r2 — ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции с «+» на «-«):

r1 — значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. f(r1)=minr0>;

r2 — значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV, т.е. f(r2)=maxr Следующая > >>

Источник

Внутренняя норма доходности (IRR) инвестиционного проекта – что это такое и как рассчитать

Формулы и примеры расчетов IRR

Рассчитать IRR можно четырьмя способами: по формуле, пользуясь встроенной функцией Excel, графическим методом и с помощью онлайн-калькулятора.

Практика инвестирования показывает, что для правильной оценки перспектив финансирования проекта необходимы предварительные расчеты. Важнейшим показателем служит внутренняя норма доходности. Норма эта учитывает приведенные значения сумм капитала и входящих денежных потоков, и в конечном счете определяет точку безубыточности инвестиции.

Статья посвящена экономическому смыслу понятия IRR и тому, как рассчитать этот показатель.

Что такое IRR инвестиционного проекта и зачем он нужен

Объяснить, что это такое – внутренняя норма доходности (IRR), можно легко и простыми словами. Отечественная и мировая экономика давно применяет этот показатель, хотя называется он по-разному: внутренним коэффициентом окупаемости (ВКО), внутренней ставкой дохода предприятия (ВСДП), внутренней нормой доходности (ВНД) и т. д.

С английского языка термин переводится как «внутренняя ставка возврата» (Internal Rate of Return, сокращенно IRR), что, вероятно, наиболее точно характеризует смысл и сущность понятия.

Под внутренней нормой прибыльности понимается предельная ставка доходности проекта, обеспечивающая дисконтированную самоокупаемость.

Все кажется понятным, но лаконичность этой формулировки требует некоторых пояснений.

Все денежные потоки вокруг проекта, а именно входящие (прибыли от коммерческой деятельности со знаком плюс) и исходящие (затраты на реализацию со знаком минус), должны в сумме давать ноль, что показывает их взаимную компенсацию, то есть самоокупаемость.

Слово «дисконтированная» означает, что каждый чистый денежный поток необходимо привести к разным процентным ставкам, действующим на протяжении периода инвестирования. Имеются в виду банковские проценты, индекс инфляции, уровень девальвации (в случае валютных вложений) и т. д.

Внутренняя норма окупаемости инвестиций учитывает специальный поправочный коэффициент. Это ставка дисконта, показывающая, насколько эффективно используется капитал по сравнению с другими вариантами вложений в бизнес за тот же временной период.

Исходя из приведенного выше определения можно сформулировать цели вычисления внутренней нормы доходности.

Первый способ применения показателя IRR – оценка прибыльности инвестиции. Чем выше значение, тем предпочтительней данный проект.

Второе приложение показателя – определение максимальных годовых ставок привлечения заемного капитала. Особенно важное значение IRR приобретает в случае банковского кредитования финансирования проекта. Если процентная ставка по займу выше запланированной рентабельности, разница между суммами исходящих и входящих денежных потоков приобретет отрицательное значение, что означает убыток.

Как рассчитать внутреннюю норму доходности

Расчет IRR можно производить четырьмя способами: вручную по формуле, пользуясь встроенной функцией Excel, графическим методом и с помощью онлайн-калькулятора.

Уравнение с нулевой суммой будет приведено ниже.

Математический способ – наиболее простой для понимания, но технически бывает довольно сложным.

В форму Excel необходимо внести нужные данные о затратах и предполагаемых уровнях доходности инвестиции, используя в качестве источника бизнес-план.

График зависимости IRR от сумм дисконтированного дохода наиболее нагляден. Диаграмма строится в равных промежутках времени, откладываемых по оси абсцисс. По ординате откладываются суммы дисконтированного дохода и приведенных расходов. Точка безубыточности рассчитывается как пересечение линии графика с нулевым уровнем.

Формула внутренней нормы доходности и пример расчета

Исходной формулой для вычисления внутренней нормы доходности служит следующее уравнение:

• NPV – чистая приведенная стоимость проекта;
• N – количество расчетных периодов (обычно лет);
• T – номер расчетного периода;
• IS – затраты на проект в первоначальном периоде (стартовый размер инвестиции) и последующие вложения;
• IRR – внутренняя норма прибыльности.

Предельно низкая внутренняя норма прибыльности соответствует значению NPV, равному нулю. Иными словами, текущая стоимость, рассчитанная по ставке доходности IRR, должна соответствовать самоокупаемости.

После преобразования приведенной выше формулы можно найти минимальный показатель внутренней нормы прибыльности:

• IRRmin – минимальная внутренняя норма прибыльности;
• N – количество расчетных периодов;
• IS T – размеры инвестиций по каждому периоду;
• IS – общая сумма инвестиции.

Для наглядности применения этой формулы имеет смысл рассмотреть пример расчета.

Объект инвестирования – недвижимость – квартира, сдаваемая в аренду. На ее приобретение должна быть потрачена сумма 1,5 млн руб. Прогнозируется поступление арендной платы по следующему графику:

• 1-й год – 620 тыс. руб.
• 2-й год – 632 тыс. руб.
• 3-й год – 790 тыс. руб.

Суммы входящих потоков и стоимость квартиры приведены в денежном выражении (тысячах рублей). При подстановке данных в формулу получается:

При внутренней норме доходности равной 8% использование заемного капитала, привлеченного по более высокой ставке, нерентабельно. Даже обычный депозитный вклад в банке, как финансовый инструмент, может принести предпринимателю бо́льшую прибыль, чем сдача квартиры в аренду на таких условиях.

Расчет внутренней нормы доходности в таблице Excel

Приведенная выше формула расчета показателя IRR понятна и удобна, но если проектов несколько и условия более сложны, задача становится излишне трудоемкой. К счастью, есть инструмент определения эффективности инвестиций в Excel. Пример с пояснениями того, как посчитать внутреннюю норму прибыльности, будет рассмотрен ниже.

В программе Эксель есть встроенная функция ВСД – ею и надлежит пользоваться. При этом следует придерживаться простых правил и выполнить несложную последовательность действий.

Для расчета IRR в Excel необходимо:

1. Войти в программу.
2. Создать книгу с таблицей денежных потоков и их датами. Одно из значений обязательно должно иметь отрицательное значение – это сумма инвестиции, то есть затраты на реализацию. В таблице могут содержаться данные нескольких проектов для сравнения.
3. Выбрать функцию IRR в мастере функций (для русского интерфейса ВНД или ВСД) нажатием кнопки fx.
4. Отметить участок нужного столбца с данными, подлежащими анализу. В строке появится что-то вроде «IRR(B4:B:12, 7,2%)».
5. Нажать кнопку «OK».

Графический метод определения внутренней нормы доходности IRR

Графический метод расчета внутренней нормы прибыли отличается от ранее описанных большей наглядностью и приблизительностью. Для построения диаграммы также необходимы вычисления, но требования к их точности ниже. Впрочем, это не имеет большого значения потому, что исходные данные тоже страдают существенным «разбегом».

Суть метода состоит в возможности определить величину предельного показателя IRR как точки пересечения линии графика с осью ординат, то есть нулевым значением доходности. Графики зависимости приведенной стоимости от ставки дисконтирования строятся вручную или с использованием возможностей функции диаграмм Excel. Их может быть несколько, и проект того из них, у которого значение предельной доходности инвестиции окажется дальше от нулевой точки, будет признан более предпочтительным.

Онлайн-калькуляторы внутренней нормы доходности

Существуют и другие способы, как найти IRR инвестиционного проекта даже не прибегая к таблицам Excel. В интернете доступны специализированные калькуляторы, в которые встроены готовые алгоритмы. Пользователю не нужно вникать в то, по каким формулам и как считают внутреннюю норму прибыльности эти инструменты: достаточно внести суммы денежных потоков.

Анализ полученных данных

Итак, внутренняя норма окупаемости инвестиций вычислена, и теперь требуется ее расшифровка. Понятно, что проект с большим показателем окупается быстрее, однако этот же смысл имеет и всем известный критерий прибыли, то есть средняя норма рентабельности. Отрицательный IRR явно указывает на убыточность вложения, и означает, что его сумма превышает экономический эффект.

Может ли быть внутренняя норма окупаемости больше 100 процентов? Теоретически да, но на практике такое случается крайне редко. Каково же в таком случае нормальное значение IRR?

Однозначного ответа на вопрос о том, какой должен быть этот показатель нет. Определение его приемлемого уровня возможно только в сравнении. IRR обязательно должен быть больше ставки дисконтирования RT. Если это не так, то проект вряд ли стоит того, чтобы в него инвестировать средства. Более подробно:

• IRR меньше RT – проект будет явно убыточным для инвестора;
• IRR равен RT – вложения только окупятся, но дохода не принесут;
• IRR больше RT – ожидается прибыль.

Сравнение возможно также с уровнем минимальной ожидаемой доходности компании-инвестора, а она в каждой фирме своя.

Преимущества и недостатки показателя IRR

Внутренняя норма прибыльности, к сожалению, сама по себе и в отрыве от других показателей не может исчерпывающе характеризовать доходность инвестиции.

Во-первых, она не учитывает эффекта рефинансирования получаемого дохода за счет прибыли.

Во-вторых, будучи величиной относительной, IRR не демонстрирует сумм в денежном выражении, а проценты не всегда отражают нужную инвестору информацию.

В-третьих, вложения дополнительных средств требуют повторных расчетов, в связи с чем возникает несколько значений одного и того же показателя IRR.

Вместе с тем, у нормы прибыльности как характеристики ожидаемой эффективности инвестиции есть и несомненные достоинства.

Показатель незаменим при сравнении нескольких проектов в разных временных периодах независимо от сумм финансирования.

Ставка дисконтирования может не браться в учет, так как в формулах она не фигурирует.

Отличие модифицированной внутренней нормы прибыли MIRR от IRR

Некоторые недостатки показателя IRR могут быть нивелированы несколько усложненным вариантом формулы. Внутренняя норма рентабельности в модифицированном варианте предполагает устранение неопределенностей, возникающих при нескольких траншах инвестирования в нестандартных условиях.

Методология расчета модифицированной внутренней нормы доходности MIRR основана на следующих положениях:

• Приведение денежных положительных потоков (доходов) на расчетную дату завершения инвестируемого проекта. Для этого используется ставка WACC, формируемая средневзвешенной стоимостью капитала.
• Приведение отрицательных денежных потоков (первичной и последующих инвестиций) на начальную дату проекта по ставке дисконтирования.
• Величина MIRR равна норме дохода, соответствующей самоокупаемости проекта на дату его завершения.

В конечном виде формула модифицированной внутренней нормы прибыли выглядит так:

• MIRR – модифицированная внутренняя норма прибыли;
• N – инвестиционный период в годах;
• DF – прибыли от инвестиции;
• DC – суммы инвестиций;
• WACC – сумма средневзвешенной стоимости капитала;
• R – ставка дисконта;
• i — номер периода.

Несколько большая математическая громоздкость формулы обеспечивает высокую точность расчетов за счет того, что в ней учитывается возможность реинвестирования прибыли по ставке дисконтирования. Применение Excel снижает трудоемкость при использовании функции МВСД (MIRR).

При сравнении взаимоисключающих проектов возможно использование методики MIRR, если суммы первоначальных вложений приблизительно равны, а горизонты инвестирования имеют примерно одинаковую продолжительность.

Недостатком этой формулы является низкая вероятность стабильности значения ставки реинвестирования на протяжении всего инвестиционного периода.

Источник