По условиям контракта доходность кредита должна составлять 24 годовых

Финансовая эквивалентность обязательств

Эквивалентность сложных ставок

Рассмотрим только соотношение эквивалентности для ставок i, j и i, d. Имеем

,

.

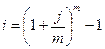
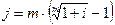
Эквивалентность i и d:

,

.

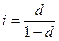
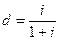
Приведем еще ряд полезных соотношений, которые можно получить на основе приведенных выше формул с учетом того, что :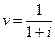

,

,

.

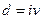
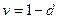
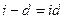
В пяти формулах, представленных выше время (срок) не играет никакой роли.

ПРИМЕР. При разработке условий контракта стороны договорились о том, что доходность кредита должна составлять 24 % годовых. Каков должен быть размер номинальной ставки при начислении процентов ежемесячно и поквартально?

; .

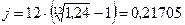
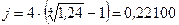
На практике нередко возникают случаи, когда нужно заменить одно денежное обязательство другим, например, с более отдаленным сроком платежа, или объединить несколько платежей в один и т. д. Такие задачи решают на основе принципа финансовой эквивалентности обязательств. Эквивалентными считаются такие платежи, которые, будучи «приведенными» к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения платежа (если дата относится к будущему). Если при изменении условий контракта указанный принцип не соблюдается, то одна из сторон контракта терпит ущерб, размер которого можно заранее определить.

Принцип финансовой эквивалентности лежит в основе значительного числа методов количественного финансового анализа. В наиболее простом проявлении этот принцип следует из формул наращения и дисконтирования, связывающих величины P и S. Сумма P эквивалентна сумме S при принятой процентной ставке и методе начисления процентов.

Две суммы S₁ и S₂, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Замена S₁ и S₂ в этих условиях формально не изменяет отношения сторон договора.

ПРИМЕР. На принципе эквивалентности основывается сравнение разновременных платежей. Имеется два обязательства. Условия первого: выплатить 400 тыс. руб. через 4 месяца; условия второго: выплатить 450 тыс. руб. через 8 месяцев. Можно ли считать их равноценными?

Т. к. платежи краткосрочные, то при дисконтировании на начало срока применим простую ставку, равную, допустим, 20 %. Получим:

тыс. руб.

тыс. руб.

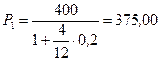
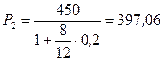
Т. о., сравниваемые обязательства не являются эквивалентными при заданной ставке и в силу этого не могут адекватно заменять друг друга.

Сравнение платежей предполагает использование некоторой процентной ставки и, следовательно, его результат зависит от ее величины. Однако, что практически весьма важно, эта зависимость не является столь жесткой, как это может показаться на первый взгляд. Допустим, сравниваются 2 платежа S₁ и S₂ со сроками n₁ и n₂, причем, S₁ P₁ справедливо при любом уровне процентной ставки, который меньше 42,8 %.

Если дисконтирование производится по сложной ставке, то критическую ставку найдем из равенства

.

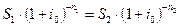
Получим .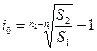

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Финансовая математика

Особенности расчета выручки исходя из суммы векселя. Определение ссуды исходя из авансовых процентов. Исследование особенностей схемы начислений по депозиту. Нахождение сроков удвоения первоначальной суммы вклада для простой и сложной процентной ставки.

Рубрика	Финансы, деньги и налоги
Вид	задача
Язык	русский
Дата добавления	02.10.2015
Размер файла	17,2 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Вексель на 12000 руб., погашаемый через 80 дней, продан банку, который установил простую учетную ставку 14% годовых. Какой будет выручка? (Используйте 360/360)

P — сумма, которую получает владелец векселя при его учете

F — наращенная сумма (номинальная стоимость векселя);

n — количество периодов продолжительности финансовой операции

d — простая учетная ставка

F = 12000; n = 80/360, d = 0,14 получим:

Р = 12000(1-0,14 80/360)=11626.67

Векселедержатель получит от банка 129,89 тыс. руб.

Комиссионные банка ( или дисконт) определяются по формуле D= F — P

D= F — P= 12000-11626.67=373.33

Клиент банка намеревается получить ссуду 100 000 руб. на 120 дней. Если банк начисляет 16 % процента авансом, какую сумму должен попросить клиент?

F = P*(1+16/365/100)120 = P*1.054

Клиент должен попросить 105400р, тогда, при вычете процентов авансом, он получит 100000.

Вклад 100 тыс. руб. сделан на 5 лет по схеме сложных процентов. Найдите итоговую сумму, которую получит вкладчик, если: а) процентная ставка остается неизменной в течение 5 лет и составляет 11% годовых; б) процентная ставка составляет 10,5% годовых, начисляемых ежедневно; в) процентные ставки начисляются 1 раз в год и составляют по годам соответственно 11%, 10.5%, 10%, 10%, 9% годовых; г) процентные ставки начисляются m раз в год и составляют по годам соответственно j12=11%, j6=10.5%, j4=10%, j4=10%, j2=9% годовых; д) процентная ставка составляет 10 % годовых, начисляемых непрерывно.

А) Процентная ставка 11%, начисляется раз в год

Схема начислений по депозиту

Базовая сумма начисления

Проценты по депозиту

Итоговая сумма с учетом процентов

б) процентная ставка составляет 10,5% годовых, начисляемых ежедневно; вычислим итоговую сумму

Итоговая сумма S=173310.74

в) г) процентные ставки начисляются m раз в год и составляют по годам соответственно j12=11%, j6=10.5%, j4=10%, j4=10%, j2=9% годовых;;

Схема начислений по депозиту

Базовая сумма начисления

Проценты по депозиту

Итоговая сумма с учетом процентов

д) процентная ставка составляет 10 % годовых, начисляемых непрерывно.

Клиент банка должен вернуть через 3 года сумму 150 тыс. руб. Клиент и банк пересмотрели условия договора: клиент решил вернуть долг сейчас. Сколько должен вернуть клиент, если: а) процентная ставка остается неизменной в течение 3-х лет и составляет 17% годовых; б) процентная ставка составляет 16,5% годовых, начисляемых ежедневно; в) процентные ставки начисляются 1 раз в год и составляют по годам соответственно 17%, 16.5%, 16% годовых; г) процентные ставки начисляются m раз в год и составляют по годам соответственно j12=16,5%, j6=16%, j4=15,5% годовых; д) процентная ставка составляет 16% годовых, начисляемых непрерывно.

В исходный момент клиент должен банку некую сумму Х.

Если на сумму Х в течение трех дет начисляются сложные проценты. Ставка 17% годовых, то можно записать уравнение

В исходный момент клиент должен уплатить 93655.6р.

Если при ставке 16,5% проценты начисляются ежедневно, то

X = 150/(1+17/12/30/100)1080 = 91446

Если процентные ставки начисляются 1 раз в год и составляют по годам соответственно 17%, 16.5%, 16% годовых

X = 150000/1.17/1.165/1.16 = 94868.4

Если процентные ставки начисляются m раз в год и составляют по годам соответственно j12=16,5%, j6=16%, j4=15,5% годовых;

X = 150000/(1+16.5/12/100)12/(1+16/6/100)6/(1+15.5/4/100)4 = 93840.8

Если процентная ставка составляет 16% годовых, начисляемых непрерывно.

X = 150000/e0.16*3 = 92817.5

Господин Петров положил 2 года назад 600 тыс. руб. в банк, выплачивающий проценты по ставке j12=9% годовых. Схема вложений предусматривает возможность снятия денег без потери процентов. Восемь месяцев тому назад он снял со счёта 400 тыс. руб., а сегодня снял ещё 100 тыс. руб. Через 3 месяца он желает вложить некоторую сумму так, чтобы через год от сегодняшнего момента закрыть счёт, получив 500 тыс. руб. Какую сумму он должен вложить?

Начальная сумма 600000

Через 14 месяцев

S = 600000*(1+9/12/100)14 = 666165.3

S=666165.3 — 400000 = 266165.3

Через 8 месяцев после снятия:

S = 266165.3 * (1+9/12/100)8 = 282560,8

S = 282560.8 — 100000=182560.8

Через три месяца сумма будет

S = 182560.8*(1+9/12/100)3 = 186699.3

Еще через 9 месяцев сумма будет

S = 186699.3 * (1+9/12/100)9 = 199686.25

Определим, какую сумму нужно положить на счет за 9 месяцев до закрытия счета, чтобы в момент закрытия на счету было 500000р.

(500000-199686,25)/ (1+9/12/100)9 = 280782.3

Сумма, которую нужно добавить на счет, составляет 280782,3р

Найти сроки удвоения первоначальной суммы вклада для простой и сложной процентной ставки 12% годовых?

Для простой процентной ставки:

процентный ставка вексель вклад

При простой процентной ставке сумма удвоится через 8,3 лет

Для сложной процентной ставки:

При сложной процентной ставке 12%, начисляемой ежегодно, первоначальная сумма удвоится через 6,1 лет.

При разработке условий контракта стороны дого-ворились о том, что доходность кредита должна составлять 24% годовых. Каков должен быть размер номинальной ставки при на-числении процентов ежемесячно, поквартально?

Если проценты начисляются ежемесячно, то номинальная ставка вычисляется из уравнения

Если проценты начисляются ежеквартально, то номинальная ставка вычисляется из уравнения

Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%?

Поквартальное начисление процентов:

F = P*(1+20/4/100)4 = P*1.2155

Непрерывное начисление процентов:

D = ln(1.2155) = 0.195156

Непрерывная ставка должна составлять 19,5%

Размещено на Allbest.ru

Подобные документы

Расчет первоначальной величины кредита и начисление простых процентов на заданную сумму. Подсчет суммы, полученной предъявителем векселя и величины дисконта банка. Нахождение суммы, которую предприниматель должен вернуть в банк по окончанию срока ссуды.

контрольная работа [25,3 K], добавлен 25.02.2012

Определение выручки от досрочного погашения векселя; понятие дисконта. Составной итог срочного депозита с конвертируемой поквартально норме процента. Зависимость суммы вклада от процентной ставки. Расчет нормы процента для накопления инвестиционной суммы.

контрольная работа [19,1 K], добавлен 04.11.2013

Изменение суммы к получению при выплате простых процентов каждый месяц. Определение точным и приближенным способами суммы ссуды, полученной клиентом. Определение эквивалентности простой годовой ставки. Определение размера доходов от страховых взносов.

контрольная работа [24,2 K], добавлен 21.06.2014

Методика определения суммы платежа с применением ставки сложных процентов. Расчет доходности операции для кредитора в виде простой, сложной процентной и учетной ставки. Вычисление предпочтительного варианта вложения денег при заданных процентных ставках.

контрольная работа [38,1 K], добавлен 26.03.2013

Накопление капитала по схеме простых процентов. Определение суммы, полученной при учете обязательства. Расчет времени, за которое происходит утроение суммы при начислении сложных процентов. Расчет реальную ставку при размещении средств на год под 35%.

контрольная работа [85,3 K], добавлен 25.03.2014

Источник

Повышение оригинальности

Предлагаем нашим посетителям воспользоваться бесплатным программным обеспечением «StudentHelp», которое позволит вам всего за несколько минут, выполнить повышение оригинальности любого файла в формате MS Word. После такого повышения оригинальности, ваша работа легко пройдете проверку в системах антиплагиат вуз, antiplagiat.ru, РУКОНТЕКСТ, etxt.ru. Программа «StudentHelp» работает по уникальной технологии так, что на внешний вид, файл с повышенной оригинальностью не отличается от исходного.

Работа № 111822

Наименование:

Контрольная Эквивалентность платежей, процентной и учетной ставок

Информация:

Тип работы: Контрольная. Предмет: Эконом. теория. Добавлен: 19.03.18. Год: 2018. Страниц: 16. Уникальность по antiplagiat.ru:

Описание (план):

Содержание
5. Эквивалентность платежей, процентной и учетной ставок 3
Задачи 7
Список используемой литературы 17

?
5. Эквивалентность платежей, процентной и учетной ставок
Ставки, обеспечивающие равноценность финансовых последствий называются эквивалентными или релятивными.
Равноценность финансовых последствий может быть обеспечена, если наблюдается равенство множителей наращения.
Если в выражениях
простая процентная ставка
;
наращенная сумма по учетной ставке

Если , то множители наращения равны
, тогда
Если срок ссуды меньше года, то и эквивалентность определяется для двух случаев равных временных баз и разных временных баз.
Если временные базы одинаковы ( ), то формулы имеют вид:

Если начисление процентов по ставке i производится при базе 365, а по ставке d при базе 360, то справедливо:

Пример
Вексель учтен в банке по учетной ставкой 8% в день окончания срока его обращения = 200 (k=360). Определить доходность этой операции по ставке простых процентов (k=365).

Эквивалентность простых и сложных процентных ставок
При начислении процентов один раз в год определяется по формулам:
– простая ставка:
– сложная ставка:
Пример
Какой сложной годовой ставкой можно заменить простую ставку 18% (k=365) не изменяя финансовых последствий . Срок операции – 580 дней.

Эквивалентность простой процентной ставки и сложной ставки.
При начислении m раз в году определяется по формуле:

Пример
При разработке условий контракта стороны договорились, что доходность кредита должна составлять 24%. Каков должен быть размер номинальной ставки при начислении процентов ежемесячно, поквартально.

Эквивалентность простой учетной ставки и ставки сложных процентов определяется по формуле:

Эквивалентность номинальной ставки сложных процентов при начислении процентов m раз в год и простой учетной ставки определяется по формулам:

Эквивалентность сложных ставок определяется по формулам:

Эквивалентность сложной учетной ставки и номинальной сложной процентной ставки при начислении процентов m раз в году определяется по формулам:

Эквивалентность непрерывных и дискретных ставок:

Эквивалентность силы роста и номинальной ставки:

При дискретном и линейном изменении силы рост, а так же если она изменяется с постоянным темпом эквивалентную зависимость со ставками сложных процентов можно выразить формулами:

Эквивалентность силы роста и учетных ставок для постой учетной ставки определяется по формулам:

Для сложной учетной ставки:
;
Замечание. Используя формулы эквивалентности дискретных и непрерывных ставок можно представить результаты применения непрерывных процентов в виде общепринятых характеристик.
?
Задачи
Исходные данные:
Первоначальная сумма – 38 тыс. руб.
Процентная ставка (учетная) – 9%
Наращенная сумма – 45 тыс. руб.
Уровень инфляции – 13 %
Период начисления – 38 мес.

Рассчитайте наращенную сумму с исходной суммы при размещении ее в банке на условиях начисления: а) простых и б) сложных процентов, если периоды наращения 90 дней, 180 дней, 1 год, 5 лет, 10 лет.
Решение:
PV= 38 тыс. руб.
i = 9%
Простой процент: I=PV*i*n; FV=PV(1+i*n)
Схема начисления 90 дней
(n=90/360=0,25) 180 дней
(n=180/360=0,5) 1 год
(n=1) 5 лет
(n=5) 10 лет
(n=10)
Простые % 38855 39710 41420 55100 72200
Сложный процент: FV=PV(1+i/100)n
Схема начисления 90 дней
(n=90/360=
1/4) 180 дней
(n=180/360=
1/2) 1 год
(n=1) 5 лет
(n=5) 10 лет
(n=10)
Сложные % 38827,57 39673,16 41420 58467,
71 89959,82

2. Инвестор имеет возможность выбора вложить свои средства в банк сроком на один год с выплатой: 25 % ежеквартально, или 30 %, но 1 раз в четыре месяца, или 45 %, но 2 раза в год, а также в размере 100 % с выплатой 1 раз в год. Определить, какой наиболее выгодным является вариант вложения денежных средств.
Решение:
PV = 38000 руб.
Решение.
Применим формулу наращения сложными процентами:

25 % ежеквартально
FV=38000*(1+0,25/4 )^(1*4)=48428,31
30 % 1 раз в четыре месяца
FV=38000*(1+0,3/3 )^(1*3)=50578
45 % 2 раза в год
FV=38000*(1+0,45/2 )^(1*2)=57023,75

100 % с выплатой 1 раз в год
FV=38000*(1+1)^1=76000
Ответ: вариант «г» является наиболее выгодным, т.к. приносит наибольший доход за счет наибольшей процентной ставки

3. Рассчитайте будущую стоимость для следующих ситуаций:
а) 5 лет, 8 % годовых, ежегодное начисление процентов;
б) 5 лет, 8 % годовых, полугодовое начисление процентов;
в) 5 лет, 8 % годовых, ежеквартальное начисление процентов.
Решение:
PV= 38 тыс. руб.
n = 5
FV= PV (1+i/m)n.m ,
где m – число наращений в год
a) FV = 38000 (1+ 0,8/1)5 = 718035,84 руб.
б) FV = 38000 (1+ 0,8/2)5*2 = 1099167,69 руб.
в) FV = 38000 (1+ 0,8/4)5*4 = 1456828,8 руб.

4. Предприятие получило кредит на один год с условием возврата наращенной суммы. Рассчитайте процентную ставку.
Решение:
Предприятие получило кредит на 1 год в размере 38000 руб. с условием возврата 45000 руб. Рассчитать простую процентную ставку
45000 = 38000 * (1 + х), х – годовая процентная ставка
45 = 38 * (1 + х)
38 + 38х = 45
38 х = 7
Х = 7 / 38 = 0,1842105263 * 100 % = 18,42 %

5. Банк выдал ссуду на 2 года из расчета 10 % годовых с условием ежеквартальной капитализации процентов. Определить наращенную сумму долга.
Решение:
S = P * (1 + j / m) mn
где j/m – ставка за период, исчисленная на основе базовой (номинальной ставки j) и числа раз начислений процентов в году (m); mn – число процентных периодов, исчисленное на основе числа раз начислений процентов в году (m) и срока финансовой операции в годах (n) или не в годах (t/Y). P – первоначальный капитал. S – наращенный капитал.
S = P * (1 + j / m) mn = 38 * (1 + 0,09 / 4)4*2 = 45,404 т.р.
I = S – P = 45,404 – 38 = 7,404 т.р.
Где I – наращение.
6. Вы хотели бы удвоить имеющуюся сумму через 5 лет. Каково минимально приемлемое значение процентной ставки?
Решение:
FV = PV*(1 + r)n
В нашем случае, PV=38000, FV=76000, n=5, тогда
r=v(5&76000/38000 )-1=0.148698354997035 или 14,87 %.
Минимально приемлемое значение процентной ставки составляет 14,87%.

7. Чему должен быть равен изначальный вклад, чтобы через 3 года иметь на счете 5 млн. руб.
Решение:
Дано:
i = 9 %
FV = 5 млн. руб.
n = 3
Решение:
PV = FV1/((1+i)^n)
PV = 5000000*1/((1+0,09)^3) = 3860917,4 руб.
Изначальный вклад равен 3860917,4 руб.

8. Вексель с определенной номинальной стоимостью и сроком погашения до 20.07.03 г. предъявлен к учету 20.03.03 г. Рассчитать сумму, которую получит владелец вексель при установленной учетной ставке банка.
Решение:
Величина суммы, полученной векселедержателем, рассчитывается по формуле: и при F = 45 тыс. руб., , d = 0,09 составит:
P=45000*(1-121/360*0,09)=43638,75
Ответ. Банк выплатил 43638,75 рублей.

9. Предприятие продало товар, получив вексель номинальной стоимостью 5000 руб., сроком 75 дней с указанной процентной ставкой (проценты не входят в номинальную стоимость). Через 60 дней с момента оформления векселя предприятие решило учесть его в банке; предложенная ставка на 1% больше процентной. Рассчитайте суммы, получаемые банком и предприятием.
Решение:
Величину начисленных простых процентов составит при r = 0,09:
FV=PV(1+r*n)=5000*(1+0,09*60/360)=5075 руб.
?=75 руб.
Величина суммы, полученной векселедержателем при учете в банке, рассчитывается по формуле: и при F = 5 тыс. руб., , d = 0,18 составит:
P=5000*(1-15/360*0,1)=4979,17 руб
Дисконт Dd, полученный банком, представляет собой разность между F (номинальной величиной векселя) и P (дисконтированной величиной векселя): Dd = 5000 – 4979,17 = 20,83 руб.
Ответ: предприятие получит от эмитента дополнительный доход в виде процентов в сумме 75 руб., от банка владелец векселя получит сумму 4979,17 руб. Банк удержит комиссию за предоставление услуги 20,83 руб.

10. Тратта выдана на сумму 100 тыс. руб. с уплатой 17.11.03 г. Владелец документа учел его в банке 23.09.03 г. по учетной ставке. Определить годовую доходность операции учета по простой ставке для банка.
Решение:
Срок от момента учета до даты погашения равен 55 дням. Пусть предъявлен вексель на сумму F, тогда доход для банка составит:
F*54/360*0,09=0,0135F, а предъявитель векселя получит сумму
F-0,0135F=0,9865F. Следовательно, по формуле доходность для банка будет:
i=(0,0135F)/(0,9865F*54)*360=0,0912316=9,12%
Определим доходность банка в суммарном выражении:
0,0912316*100000=9123,16 руб.

11. Что выгоднее: положить сумму на 4 года в банк при сложной процентной ставке 15 % годовых или отдать кредитному союзу, который предлагает 14 % годовых по сложной учетной ставке на тот же срок.
Решение:
при сложной процентной ставке 15 % годовых
FV=PV*(1+r)^n=38000*(1+0,15)^4=66462,24 руб.
при сложной учетной ставке 14 % годовых
PV=FV(1-d)^n
FV=PV/(1-d)^n =38000/(1-0,14)^4 =69468,8 руб
Следовательно, предложение кредитного союза, предлагающего 14% годовых, более выгодное, чем предложение банка при 15% годовых.

12. Определить современное значение суммы в 120 000 руб., которая будет выплачена через 2 года при использовании сложных процентов при использовании сложной учетной ставки.
Решение:
Определим современное значение суммы 120000 руб. при использовании сложных процентов:
PV=FV/(1+r)^n =120000/(1+0,09)^2 =101001,6 руб.
Определим современное значение суммы 120000 руб. при использовании сложной учетной ставки:
P=F(1-d)^n=120000*(1-0,09)^2=99372 руб
Ответ: а) 101001,6 руб.; б) 99372 руб.

13. Анализируются два варианта накопления средств по схеме аннуитета:
План 1. Вносится вклад на депозит каждые полгода при условии, что банк начисляет 8 % годовых с полугодовым начислением процентов.
План 2. Делается ежегодный вклад на условиях 9 % годовых при ежегодном начислении процентов.
Определите:
1. Какая сумма будет на счете через 12 лет при реализации каждого плана? Какой план более предпочтителен?
2. Измениться ли Ваш выбор, если процентная ставка в плане 2 будет снижена до 8,5 %?
Решение:
Для определения суммы на счете через 12 лет (т.е. будущей стоимости аннуитета) можно воспользоваться формулой: .
План 1: Вносится вклад на депозит каждые полгода при условии, что банк начисляет 8% годовых с полугодовым начислением процентов.
?FV?_pst^a=19000*((1+0,08/2)^24-1)/(0,08/2)=742569,48 руб.
План 2. Делается ежегодный вклад на условиях 9% годовых при ежегодном начислении процентов.
?FV?_pst^a=38000*((1+0,09)^12-1)/0,09=765347,35 руб.
План 2а. Делается ежегодный вклад на условиях 8,5% годовых при ежегодном начислении процентов.
?FV?_pst^a=38000*((1+0,085)^12-1)/0,085=742871,49 руб.
Ответ: 1) расчет показывает, что план 2 предпочтительнее. 2) если процентная ставка в плане 2 будет снижена до 8,5% выбор не изменится, т.к. будущая стоимость плана 2 незначительно выше будущей стоимости плана 1.

14. Определите наращенную сумму аннуитета. Срок аннуитета – 7 лет. Сумма платежа – 13 тыс. руб., и на них начисляется сложный процент.
Решение:
Рента постнумерандо; R = 13 тыс. руб., n = 7, i = 0,09
FV=13000*((1+0,09)^7-1)/0,09 = 119605,65 руб = 119,606 тыс. руб.

15. Имея на счете 40 000 руб., вы прогнозируете свой доход в течение следующих двух лет в сумме 60 000 руб. и 70 000 руб. соответственно. Ожидаемая процентная ставка в эти годы будет 8 и 14%. Минимальные расходы составляют: в текущем году 20 000 руб.; в последующие годы ожидается их прирост с темпом равным годовой ставке. Рассчитайте потенциально доступную к потреблению сумму в каждом из следующих двух лет.
Решение:
Доступная к потреблению сумма в текущем году
руб.
Определим потенциально доступную к потреблению сумму в следующем году:

Определим потенциально доступную к потреблению сумму во втором году после текущего:

Ответ: потенциально доступная сумма в следующем после текущего составит 63072 руб, во 2-м году после текущего года – 123630,72 руб.

16. Участок сдан в аренду на 20 лет. Сумма годового платежа 1000 руб., причем каждые пять лет, происходит индексация величины платежа на 10%. Рассчитайте текущую цену договора на момент его заключения, если банковская процентная ставка определена.
Решение:
Представим результаты расчетов текущей цены договора в табличном виде:
Год Денежный поток Дисконтный множитель
при r = 13 % Приведенный поток
1 1000 0,8850 885
2 1000 0,7831 783,1
3 1000 0,6931 693,1
4 1000 0,6133 613,3
5 1000 0,5428 542,8
6 1100 0,4803 528,33
7 1100 0,4251 467,61
8 1100 0,3762 413,82
9 1100 0,3329 366,19
10 1100 0,2946 324,06
11 1210 0,2607 315,447
12 1210 0,2307 279,147
13 1210 0,2042 247,082
14 1210 0,1807 218,647
15 1210 0,1599 193,479
16 1331 0,1415 188,3365
17 1331 0,1252 166,6412
18 1331 0,1108 147,4748
19 1331 0,0981 130,5711
20 1331 0,0868 115,5308
Итого 23205 7619,666

Суммируя приведенные стоимости всех денежных поступлений, получим приведенную стоимость аннуитета 7619,666 рублей.

17. Директор инвестиционной компании в течение 10 лет откладывал ежегодно по 5 тыс. руб. В конце 11 года потратил 60 тыс. руб. В конце 12 года еще 75 тыс. руб. Через 20 лет директор уходит на пенсию, и хотел бы получать по 20 тыс. руб. ежегодно. Сколько он должен откладывать ежегодно с 13 по 20 год, чтобы после выхода на пенсию, в течение 20 лет, иметь ежегодную ренту в сумме 20 тыс. руб. если сложная процентная ставка будет составлять заданный %.
Решение:
Определим сумму, которая накопится в течение 11 лет с помощью формулы будущей стоимости аннуитета при условии, что r = 9%:
?FV?_pst^a=A*((1+r)^n-1)/r
?FV?_pst^a=5000*((1+0,09)^11-1)/0,09=87801,47
Определим сумму, которая останется на счете после снятия 60000 руб.:
87801,47 – 60000 = 27801,47 руб.
Определим сумму, которая накопится в 12-м году:
27801,47 * (1 + 0,09) + 5000 = 35303,6 руб.
Определим сумму, которая останется на счете в конце 12-го года после снятия 75000 руб.:
35303,6 – 75000 = — 39696,39 руб.
Определим сумму, которая накопится из остатка суммы 12-го года с 13-го по 20-й год:
-39696,39 * ( 1+ 0,09)8 = -79097,54 руб.
Определим сумму, которую требуется накопить к 20-му году:
20000 * 20 – ( -79097,54) = 479097,54 руб.
Для определения ежегодного аннуитета с 13-го по 20-й год воспользуемся формулой будущей стоимости аннуитета постнумерандо:
?FV?_pst^a=A*((1+r)^n-1)/r
A=(?FV?_pst^a)/(((1+r)^n-1)/r)=(?FV?_pst^a*r)/((1+r)^ -1)=(479097,54*0,09)/((1+0,09)^8-1)=43441,87 руб
Ответ: директор инвестиционной компании должен откладывать 44000 руб. ежегодно с 13-го по 20-й год, чтобы после выхода на пенсию, в течение 20 лет, иметь ежегодную ренту в сумме 20 тыс. руб.

18. К Вам как к менеджеру по недвижимости бизнес – центра обратилась организация с предложением арендовать офисные площади в количестве 780 м.кв. по установленной вами на основе рыночных данных цене 750 рублей за 1 м.кв. в месяц, сроком на 1 год. При этом потенциальные арендаторы предложили вам следующую схему оплаты: разовый платеж в сумме 45 000 рублей, затем, в конце 3-го, 4-го и 5-го месяцев – платежи в размере 585 000 руб., в начале 6-го, 7-го и 8-го месяцев – 580 000 рублей и в конце 12-го месяца – внесение последнего платежа в сумме 2 400 000 рублей. Проанализируйте варианты вашего решения, если на рынке аренды офисной недвижимости в вашем городе одним из условий типичного платежа является помесячное внесение арендной платы в конце каждого месяца, а ставка дисконтирования установлена.
Решение:
Для анализов решения продисконтируем денежные потоки при ставке дисконта 13%. Расчеты произведем в таблице:
Вариант 1
№ месяца Денежный поток Дисконтирующий множитель Приведенный поток
1 45000 0,8850 39825
2 — 0,7831
3 585000 0,6931 405463,5
4 585000 0,6133 358780,5
5 585000 0,5428 317538
6 580000 0,4803 278574
7 580000 0,4251 246558
8 580000 0,3762 218196
9 — 0,3329
10 — 0,2946
11 — 0,2607
12 2400000 0,2307 553680
Итого: 5940000 1864935

Вариант 2
№ месяца Денежный поток Дисконтирующий множитель Приведенный поток
1 495000 0,8850 438075
2 495000 0,7831 387634,5
3 495000 0,6931 343084,5
4 495000 0,6133 303583,5
5 495000 0,5428 268686
6 495000 0,4803 237748,5
7 495000 0,4251 210424,5
8 495000 0,3762 186219
9 495000 0,3329 164785,5
10 495000 0,2946 145827
11 495000 0,2607 129046,5
12 495000 0,2307 114196,5
Итого: 5940000 2929311

Текущая стоимость аннуитета равна:
Вариант 1: 1864935
Вариант 2: 2929311
С позиции текущей стоимости аннуитета вариант 2 более предпочтителен

19. Клиент банка занял на пять лет сумму под 8% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите общую стоимость суммы процентов к выплате.
Решение:
Для определения ежегодных платежей погашения ссуды воспользуемся настоящей стоимости аннуитета постнумерандо:
?PV?_pst^a=A*(1-(1+r)^(-n))/r
A=(?PV?_pst^a)/((1-(1+r)^(-n))/r)=(?PV?_pst^a*r)/(1-( +r)^(-n) )=(38000*0,08)/(1-(1+0,08)^(-5) )=3040/0,31942=9517,25=9500 руб
Расчеты произведем в таблице:
Год Остаток ссуды на начало года Величина годового платежа В том числе Остаток ссуды на конец года
Проценты за год Погашенная часть долга
1 38000 9500 3040 6460 31540
2 31540 9500 2523 6976,8 24563,2
3 24563,2 9500 1965,056 7534,944 17028,256
4 17028,256 9500 1362,26 8137,74 8890,52
5 8890,52 9601,76 711,24 8890,52 0
Итого 47601,76 9601,556 38000 Х
Таким образом, общая стоимость суммы процентов к выплате составляет 9601,556 руб.

20. Клиент занял на шесть лет 15000 руб. под % годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите, какой процент будет уплачен в третьем году.
Решение:
?PV?_pst^a=A*(1-(1+r)^(-n))/r
A=(?PV?_pst^a)/((1-(1+r)^(-n))/r)=(?PV?_pst^a*r)/(1-( +r)^(-n) )=(15000*0,09)/(1-(1+0,09)^(-6) )=1350/0,40373=3343,82=3300
Год Остаток ссуды на начало года Величина годового платежа В т.ч. Остаток ссуды на конец периода
% Погашенная часть долга
1 15000 3300 1350 1950 13050
2 13050 3300 1174,5 2125,5 10924,5
3 10924,5 3300 983,205 2316,79 8607,71
4 8607,71 3300 774,69 2525,31 6082,40
5 6082,40 3300 547,42 2752,58 3329,82
6 3329,82 3629,5 299,68 3329,82 0
20568,78 5568,78 15000

уплаченный процент, который составит в 3-м году = 3507,705
3507,705 / 5568,78 * 100 = 62,99
Уплаченный процент в 3-м году составит 62,99% от общей суммы процентов

?
Список используемой литературы
Багриновский К.Г. Экономико-математические метода и модели: Учебник / К.Г. Багриновский, В.Д. Матюшок. – М.: Экономистъ, 1999. – 185 с.
Бочаров П.П. Финансовая математика: Учебник / П.П. Бочаров, Ю.Ф. Касимов. – М.: Гардарики, 2002. – 624 с.
Кузнецов Б.Т. Финансовая математика: Учебное пособие / Б.Т. Кузнецов. – М.: Экзамен, 2005. – 128 с.
Кутуков В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, инвестиционных, пенсионных и страховых схем. / В.Б. Кутуков – М.: Дело, 1998. – 304 с.
Лукашин Ю.П. Финансовая математика: Учебное пособие / Ю.П. Лукашин. – М.: МФПА, 2004. – 81 с.
Малыхин В.И. Финансовая математика / В.И. Малыхин. – М.: Юнити – Дана, 2003. – 237 с.
Меньшиков С.И. Рентабельность и рента / С.И. Меньшиков // Экономическое стратегии. – 2004. – 220 с.
Четыркин Е.М. Финансовая математика / Е.М. Четыркин. – 4-е изд. — М.: Дело, 2004. – 400 с.

Смотреть похожие работы
* Примечание. Уникальность работы указана на дату публикации, текущее значение может отличаться от указанного.

Источник